考虑开模温度场分布的热冲压变形仿真方法

有限元中的算法一般分为显示和隐式两种，它们各自的特点见表5-2。对板料冲压后的回弹过程进行应力应变场的分析时，为保证回弹仿真的精度，多选择计算成本较高的隐式算法。而在对温度场进行分析时，考虑到计算的成本及经济型，在此采用显示算法。

表5-2 显隐式算法对比

对于零件开模后的应力卸载回弹过程，本书采用无模法进行模拟，即在回弹仿真开始时，先移除冲压成形过程中的模具工具，将成形终了状态的接触条件转化为反向的力学边界条件F′，并导入成形终了时刻板料的应力应变场信息作为回弹仿真过程中板料的初始状态。回弹开始时，接触反力F′作为外力场与板料内部的应力场相互平衡。设置三点约束防止板料发生刚体运动，回弹仿真过程中逐步将外力卸载至零，采用隐式增量法求解结构系统的运动学平衡方程组，得到零件开模回弹后的最终形状及应力应变场的分布。

结构系统的通用运动学平衡方程为

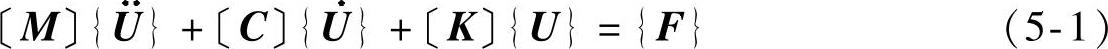
式中，〔M〕、〔C〕和〔K〕分别为结构的质量、阻尼和刚度矩阵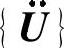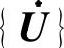；、和{U}分别为节点的加速度、速度和位移矢量^[76]；{F}为结构所受内外力的矢量合，即接触反力F′与内应力之差。

求解上述回弹过程中的平衡方程采用Newmark隐式法，假定从t到t+Δt时刻的加速度不变，取为常数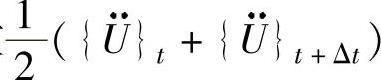，则有

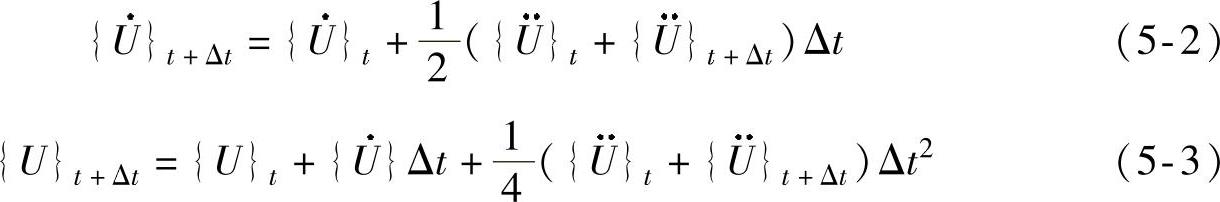
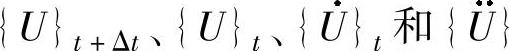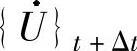由式（5-2）和式（5-3）可以得到用t表示的和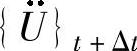的表达式，即

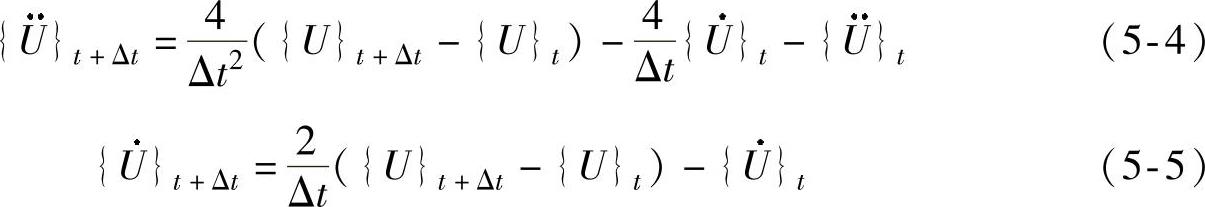
考虑t+Δt时刻的运动学平衡方程并将式（5-4）和式（5-5）代入，即可得到关于{U}_t+Δt的方程：

式中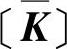，为有效刚度矩阵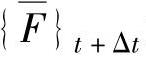；为有效载荷。

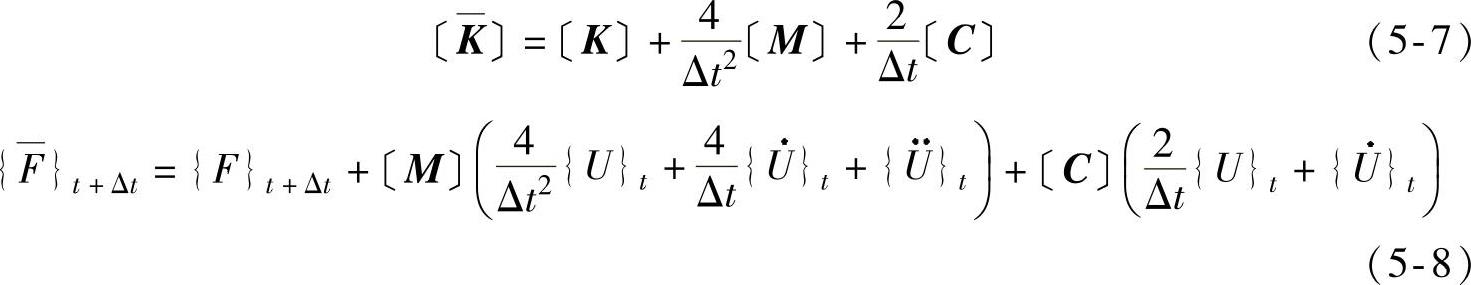
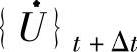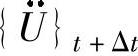由式（5-6）～式（5-8）可得{U}_t+Δt，进而可由式（5-4）和式（5-5）解出和。(www.xing528.com)

对温度场进行分析时，根据传热学的基本理论，可以推导出板料在热回弹过程中的传热微分方程^[77]：

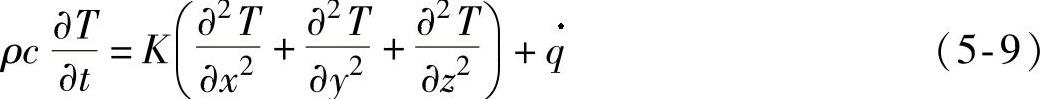
式中，ρ为材料的质量密度；c为比热容；T为材料内部任一点的瞬时温度值；t为时间；K为各向同性材料的导热系数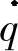；为单位体积内的热生成率。

初始条件的设定：将热冲压成形后的温度场分布信息导入作为回弹仿真分析开始时的温度场初始状态；边界条件的设定：在回弹仿真分析的过程中，主要的边界条件为板料与工作环境之间的热交换，而环境温度设定为室温，故属于第三类边界条件，即

Q=H（T_blank-T_air） （5-10）

H=h+h_s （5-11）

式中，Q为等效热流密度；H为总换热系数，由板料与空气间的对流传热系数h和辐射换热系数h_s组成；T_blank和T_air分别为板料和环境温度。

对式（5-9）进行变分和离散化可得单元瞬态温度场有限元方程的矩阵形式：

式中，C^e和K^e分别为单元的热容矩阵和热传导矩阵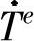；和T^e分别为单元节点温度对时间的导数向量和节点温度向量；F^e为节点的温度载荷向量^[77]。

求解上述温度场有限元方程，采用中心差分显示法，即

将式（5-13）代入式（5-12）可得

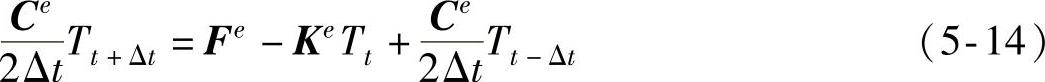
由式（5-14）即可得到某一时刻的温度T_t+Δt。