在热成形后期,由于温度的下降,组织从奥氏体转变为马氏体,因此建立更为准确的马氏体相变动力学模型,是有限元分析的必要基础。基于母相奥氏体、相变马氏体的化学自由能为温度线性函数的假设和模型[56],建立了22MnB5的高温热变形马氏体相变动力学模型。
1)能量关系。参与转变的母相奥氏体及马氏体体系的能量可用式(4-39)[57]来描述:
Gε=VAgAε(T)+VMgεM(T)+EtAh→M(VM,T) (4-39)
式中,VA为奥氏体的体积;VM为马氏体的体积;EtAh→M(VM,T)为自由能中非化学能部分。
马氏体体积分数可用式(4-40)来描述:
ζM=VM/V (4-40)
式中,V为总体积。
若只考虑向马氏体转变的奥氏体部分,淬火后材料组织成分仅为奥氏体和马氏体,不考虑其他相变即
V=VA+VM (4-41)
奥氏体体积分数可采用式(4-42)描述:
ζA=1-ζM( 4-42)
由于奥氏体向马氏体转变,所以dVA=-dVM,
ΔgεA→M=gεM(T)-gεA(T)为形变后的奥氏体向马氏体转变的化学驱动力。非化学自由能EthA→M包括以下几部分:相变时形状和体积的改变而产生的相变应变能,奥氏体/马氏体界面能,由于摩擦及相变时母相和马氏体中产生的不可逆缺陷造成的耗散能,具体可用式(4-45)来描述:
dEthA→M=(eiTkσcik+ηγT+eiTkσdik)dVM,i或k=1,2,3(4-45)式中,eiTkσcik为相变应变能,eiTk为相变应变,σcik为抵抗相变时形状及体积改变的应力;ηγT为界面能,γT为比界面能,η=dA/dVM,此界面能只在形核阶段比较重要,以后可忽略;eiTkσdik为耗散能,σdik为克服非固有耗散能所需应力。
2)基本假设。非化学自由能不随温度变化:
式中,aM、bM为表征奥氏体自由能随温度线性变化的参数;k为常数;ν为泊松比;α为材料常数,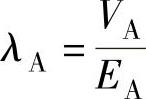 。
。
当T<Ms时,dG=0,则
相变一开始非化学自由能产生并且累积,当相变结束时非化学自由能达到饱和值,假设非化学自由能与马氏体体积为线性关系,即(https://www.xing528.com)
EthA→M=ρthA→MVM,ρthA→M=eiTkσcik+eiTkσdik (4-47)
未发生预变形的奥氏体及马氏体的化学自由能是温度的线性函数[58],假设高温预变形后的奥氏体及马氏体的化学自由能也是温度的线性函数,即
式中,aM、bM为表征奥氏体自由能随温度线性变化的参数;k为常数;ν为泊松比;α为材料常数,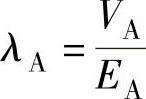 。
。
式中,aM、bM为表征马氏体自由能随线性变化的参数,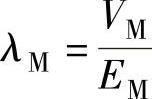 。
。
3)马氏体相变动力学计算模型。根据上述公式和4.4.1,可得
式中,aM、bM为表征马氏体自由能随线性变化的参数,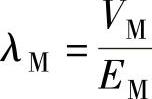 。
。
3)马氏体相变动力学计算模型。根据上述公式和4.4.1,可得
所以,初始条件T=Ms时,马氏体转变量ζ=0,则
所以,初始条件T=Ms时,马氏体转变量ζ=0,则
求解得
求解得
马氏体相变开始温度Ms是与奥氏体高温预变形应力相关的函数。若通过试验获得马氏体相变开始温度Ms、马氏体相变结束温度Mf及所对应的马氏体最终相变体积分数,可求得公式中φthA→M+(aM∗-aA∗)这项,即
马氏体相变开始温度Ms是与奥氏体高温预变形应力相关的函数。若通过试验获得马氏体相变开始温度Ms、马氏体相变结束温度Mf及所对应的马氏体最终相变体积分数,可求得公式中φthA→M+(aM∗-aA∗)这项,即
则最终考虑高温奥氏体预变形的马氏体相变动力学方程可表示为
则最终考虑高温奥氏体预变形的马氏体相变动力学方程可表示为
式中,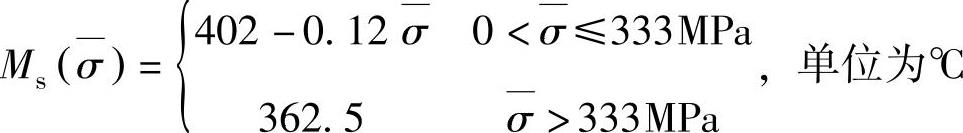 。
。
式中,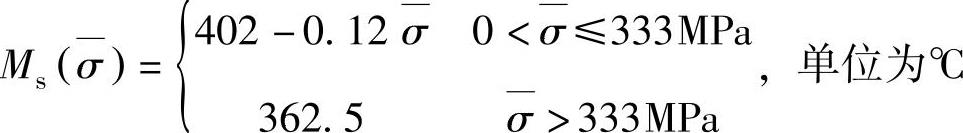 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




