形变奥氏体扩散相变的热力学分析

相变实际是自由能的变化过程，如奥氏体相（γ）向铁素体相、贝氏体相或马氏体相（α）转变的过程中是自由能由高向低的变化过程，相变的热力学分析有助于了解相变的本质过程。

Fe-∑X-C（X=Si、Mn、Ni、Mo等）合金的γ→α相变驱动力可以采用超组元（Superelement）模型来求解，将Fe-∑X视为一个超组元S，则类似于Fe-C合金^[37]。多元合金Fe-∑X-C奥氏体中产生先共析铁素体时的自由能变化可表示为

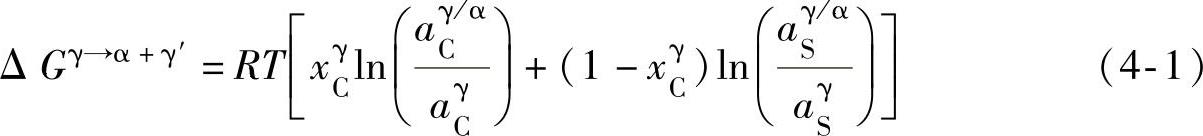
式中，x^γ_C为C在γ相中初始摩尔分数；a^γ_C和a^γ/α_C分别为C在γ相中和γ/α相界处γ相侧的活度；a^γ_S和a^γ/α_S分别为S在γ相中和γ/α相界处γ相侧的活度；R为气体常数。

超组元S在γ→α相变的自由能变化^[38]可表示为

ΔG^γ→α_S=141∑x_i（ΔT_im-ΔT_inm）+ΔG_Fe^γ→α{T-100∑x_iΔT_mⁱ} （4-2）

式中，x_i为置换型合金元素i的摩尔分数；ΔTⁱ_m和ΔT_nmⁱ分别为自由能的磁性和非磁性分量所对应的温度位移，通常称为Zener两参数，彭宁琦等^[39]对其进行了修正；“{}”表示ΔG^γ→α_Fe为T-100∑x_iΔTⁱ_m的函数；ΔG^γ→α_Fe为纯铁由γ相转变为α相时的自由能变化。本书根据张斌等^[40]文章，采用如下表达式：

ΔG^γ→α_Fe=20853.06-466.35T-0.46304T²+71.147TlnT （4-3）

α和γ相热力平衡时，根据相平衡原则，在相界处有

μ^α/γ_C=μ^γ/α_C （4-4）

μ^α/γ_S=μ^γ/α_S （4-5）

式中，μ^α/γ_C和μ^γ/α_C分别为γ/α相界处α相和γ相侧C的化学位；μ^α/γ_S和μ^γ/α_S分别为γ/α相界α相和γ相侧S的化学位。

根据Moy和Hsu^[41]文章，C在γ相中的活度为

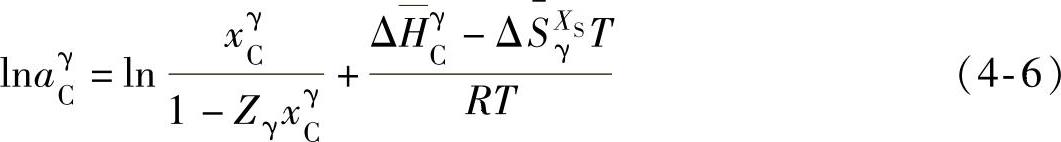
C在γ/α相界γ相和α相侧中的活度可表达为

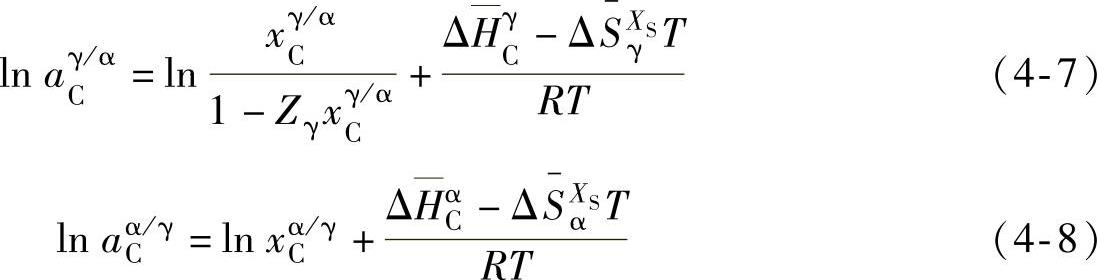
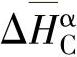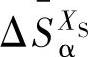式中，ΔH^γ_C和分别为C在γ相和α相中的偏摩尔焓；和分别为C在γ相和α相中的偏摩尔非配置熵。

超组元S在γ相中的活度为

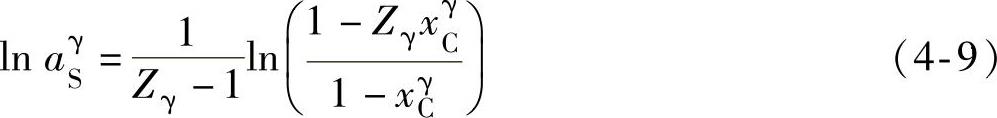
超组元S在γ/α相界两侧的活度表达式为

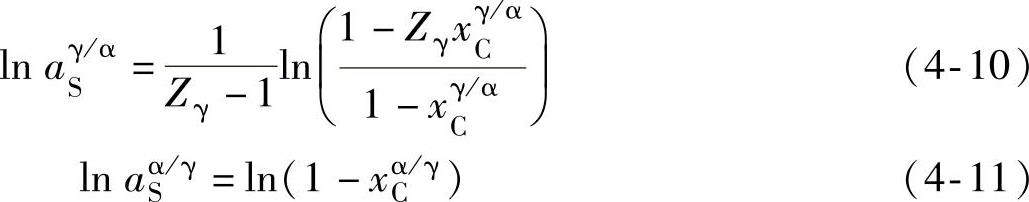
其中，

式中，ω_γ为C在γ相中的C—C交互作用能。

将式（4-7）、式（4-8）、式（4-10）和式（4-11）代入式（4-4）和式（4-5）可得(www.xing528.com)

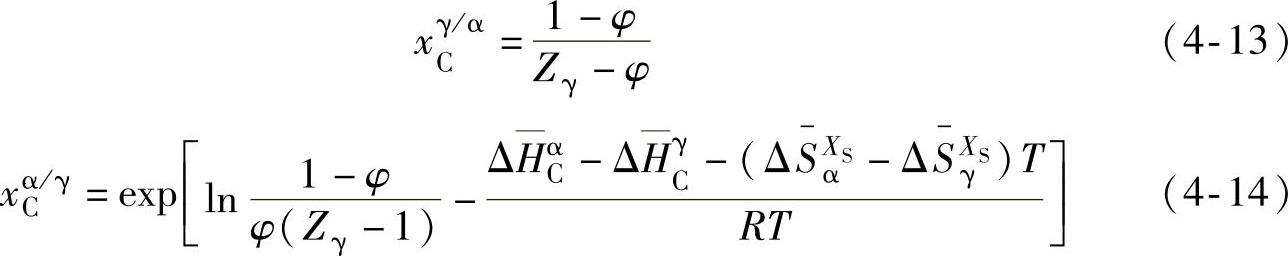
其中，

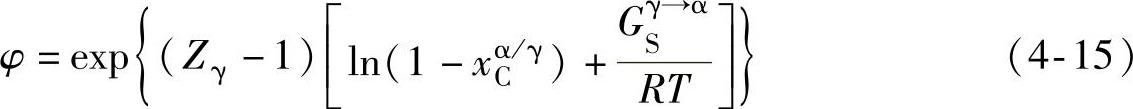
将式（4-6）、式（4-7）、式（4-9）和式（4-10）代入式（4-1）得

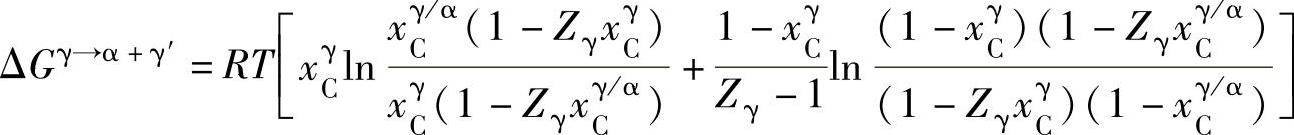
（4-16）

对式（4-13）和式（4-14）通过Newton-Raphson迭代法求解出不同温度下的x^γ/α_C^[30]，再代入式（4-16）中，可获得相变驱动力。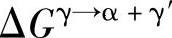

高温变形使得γ相自由能上升，导致平衡相成分和相变驱动力发生变化，变形引起的化学势增量Δμ_d，可表示为

Δμ_d=μρb²V_γ/2 （4-17）

式中，μ为剪切模量；b为Burgers矢量；V_γ为γ相的摩尔体积；ρ为位错密度，可通过流动应力式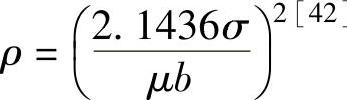计算得出。

由于变形引起自由能升高，则平衡条件式（4-4）和式（4-6）变为

μ^α/γ_C=μ^γ/α_C+Δμ_d （4-18）

μ^α/γ_S=μ^γ/α_S+Δμ_d （4-19）

式（4-14）和式（4-15）更新为

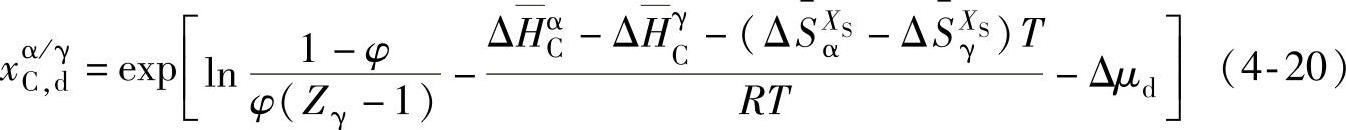
其中，

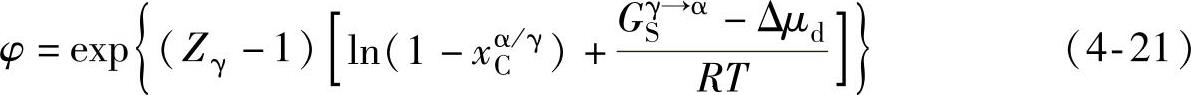
对式（4-20）和式（4-21）通过Newton-Raphson迭代法求解出变形后不同温度下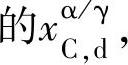再代入式（4-16）中，可获得变形后的相变驱动力。

图4-1所示为22MnB5钢板在应变速率为0.5/s时不同变形温度下及变形温度为873K时不同应变速率下的流动应力和变形储能。流动应力随应变及应变速率增加而升高，温度降低将增加流动应力。奥氏体变形后位错密度随变形条件的不同有不同程度的升高。变形条件对变形储能Δμ_d的影响类似于流动应力，但随应变的增长速率大于流动应力。图4-2所示为利用超组元模型计算得出的22MnB5钢板高温下变形储能对相变驱动力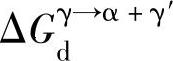和C在γ/α相界处γ相侧含量的影响。显然，变形储能的引入增加了相变驱动力，并使得γ/α相界γ相侧的碳平衡浓度上升，从而使得两相平衡区右移。

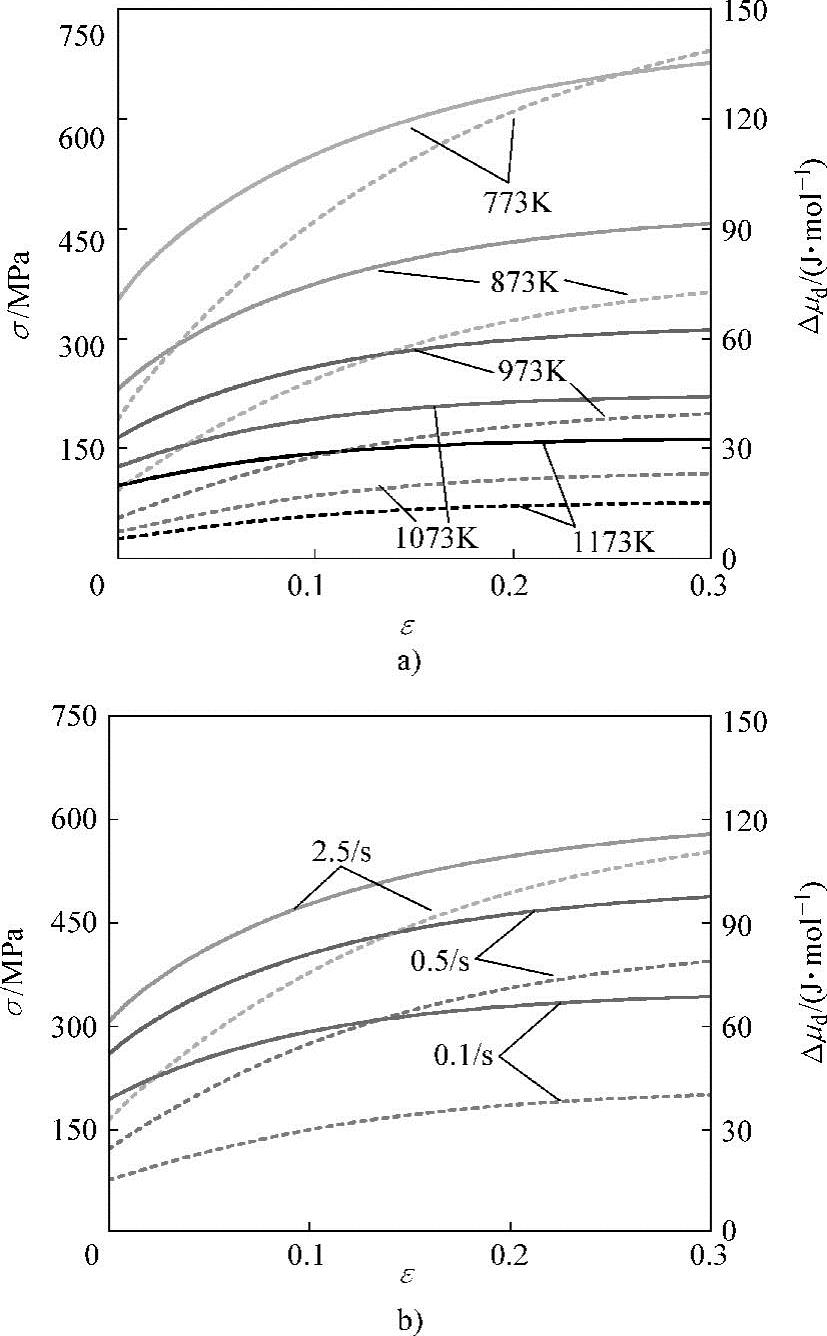
图4-1 22MnB5钢板流动应力及变形储能（实线为流动应力，虚线为变形储能）

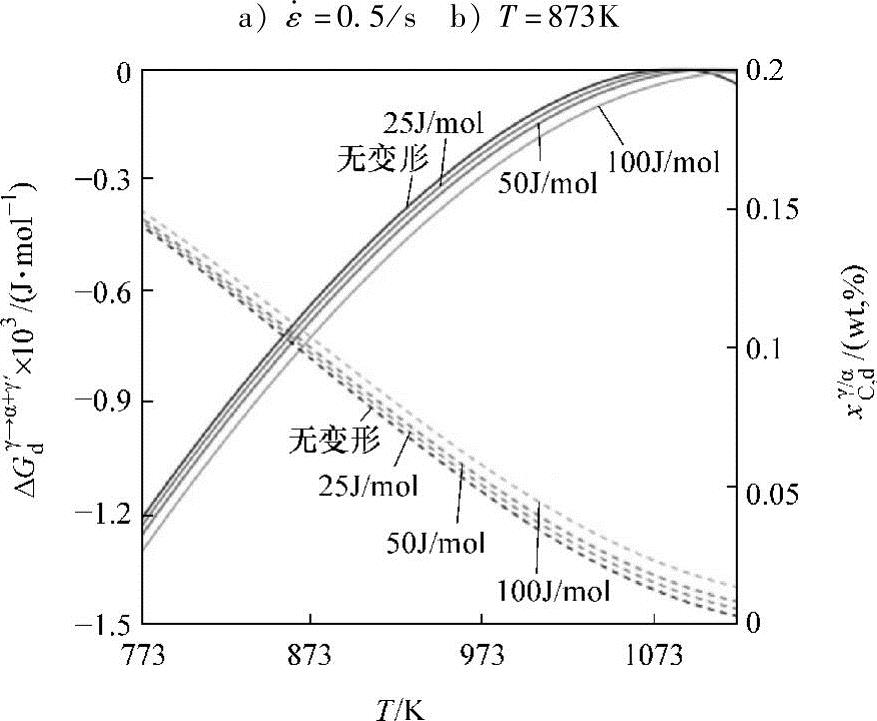
图4-2 22MnB5钢板高温下变形储能对相变驱动力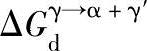和C在γ/α相界处γ相侧含量的影响（实线为相变驱动力，虚线为C的摩尔分数）