预测超高强度硼钢板热冲压成形极限模型

用理论来预测FLD都是以材料的屈服准则、本构模型和相关的流动法则为依据，通过采用不同的屈服准则和塑性本构关系，利用不同的拉伸失稳准则作为判断缩颈与破裂的条件来进行解析的。根据描述失效条件的不同，涌现出了一批成形极限理论，即Hill塑性失稳理论^[28]、S-R理论^[29]、M-K沟槽理论^[30]等。Hill关于局部缩颈的理论只在负应变比区域时可靠的，即FLD的左边。M-K沟槽理论主要被用来确定正应变比区域的极限应变。本节主要利用Hill塑性失稳理论和M-K沟槽理论对FLD的左边和右边分别进行预测。3.4.3.1 超高强度硼钢板热成形右侧成形极限的预测模型

1）M-K理论模型。M-K理论模型^[30]最初是由Marciniak等提出，经过许多学者的不断完善，M-K理论预测FLD已经成为预测薄板成形极限最常用的方法。M-K理论的核心是厚度不均性假设，通常假设板料存在初始的沟槽来表示这种不均性，如图3-19所示。厚度不均主要是由板料的局部晶粒大小变化、组织结构及合金成分等物理因素和厚度变化引起的（物理性质方面的不均可等效为板厚不均）。当这种带沟槽的薄板两端施加拉力时，变形集中在板料厚度小的槽内板料，因而，槽内板料厚度变薄比槽外板料厚度变薄快。当沟槽内板料达到平面应变状态时，材料达到最大的承载能力^[31]。

根据塑性变形中体积不变条件可获得

dε₁+dε₂+dε₃=0 （3-19）

根据A区和B区界面力平衡条件可获得

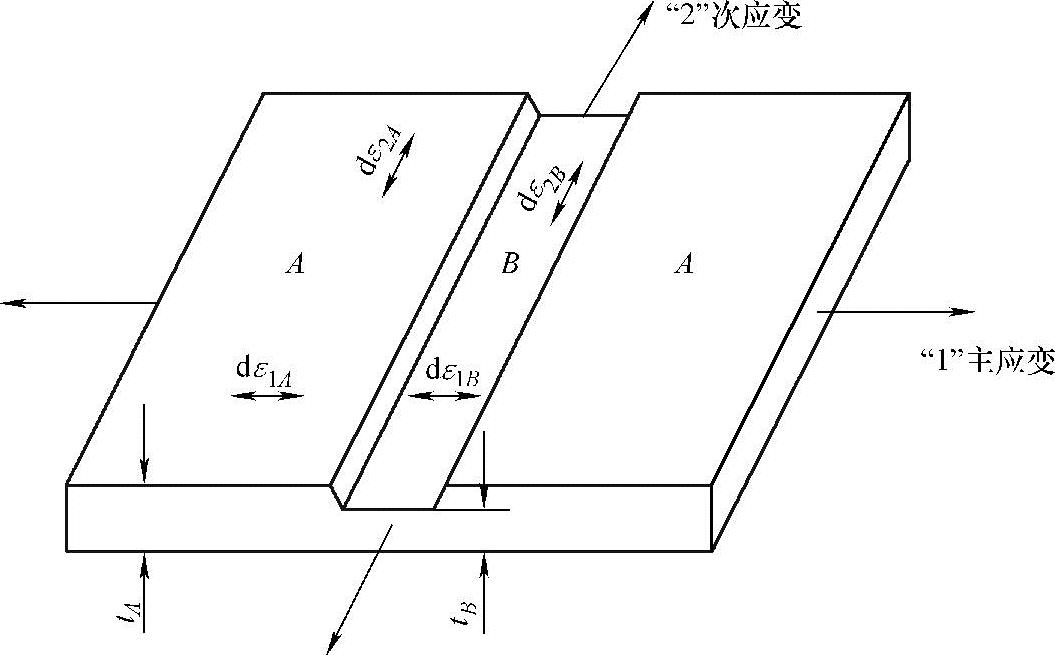
图3-19 M-K理论模型

σ^A_nntA=σ^B_nnt_B （3-20）

σ^A_nttA=σ^B_ntt_B （3-21）

式中，σ^A_nn（σ^B_nn）和σ^A_nt（σ^B_nt）分别为图3-19所示A区（B区）界面上沿法向和切向的应力分量；t_A（t_B）分别为A区（B区）板料的厚度。

A区和B区界面上应变协调条件为

dε_2A=dε_2B （3-22）

由于M-K理论的沟槽垂直于主应变方向，无论在FLD的左侧还是右侧，均与22MnB5钢板高温下缩颈方式吻合。因此，当沟槽内板料（B区）的应变状态向平面应变状态偏移时，材料达到其最大的承载能力。此时槽外材料（A区）的应变可视为板料的极限应变。因此，该模型可以作为计算硼钢板的成形极限的理论依据。

2）热成形极限计算体系框架。基于M-K理论模型和塑性成形基本理论，图3-20给出了超高强度硼钢板高温成形极限的理论计算结构。根据温度T下的材料高温力学本构方程，再寻求能够更好描述该温度下材料屈服特性的屈服准则，通过该理论计算程序就可以求得对应于温度T下的材料的FLD。

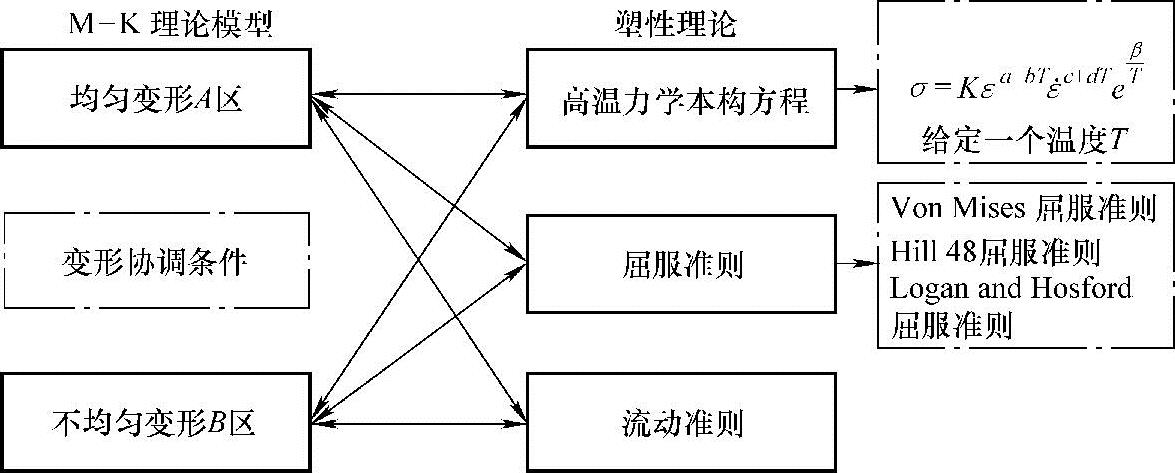
图3-20 超高强度硼钢板高温成形极限的理论计算结构

根据M-K理论，应用高温力学本构方程、屈服准则及相关流动准则，可以获得板料的极限应变。由于在成形极限左右两侧，用不同的屈服准则来预测所获得成形极限精度会有所差异，本章对Von Mises屈服准则^[32]、Hill 48屈服准则^[33]和Logan and Hosford屈服准则^[34]的影响进行了分析研究，以期获得能够准确描述该温度下材料屈服特性的屈服准则。

3）右侧成形极限预测模型。根据图3-19，A区和B区界面力平衡条件为

σ_1At_A=σ_1Bt_B （3-23）

又根据厚向应变的定义为

t_A=t_0Aexp（ε_3A） （3-24）

t_B=t_0Bexp（ε_3B） （3-25）

式中，t_0A（t_0B）和ε_3A（ε_3B）分别是A区（B区）板料的初始厚度和厚向应变。

则得到式（3-26）：

σ_1Aexp（ε_3A）=f₀σ_1Bexp（ε_3B） （3-26）

式中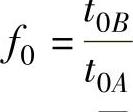，，板料的初始厚度比值。

令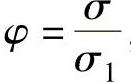，则将材料本构关系即式（3-5）代入式（3-26）得

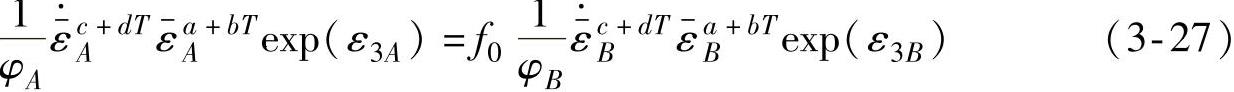
即

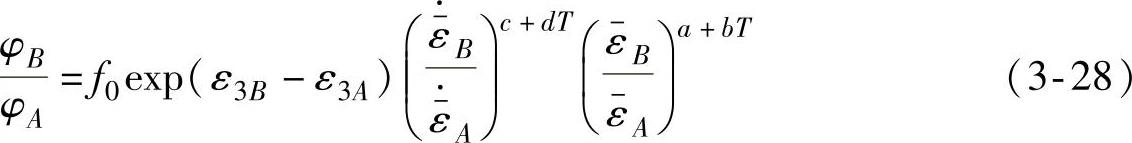
在计算过程中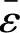，的增加是以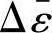连续增加的，因此，式（3-27）可表达为

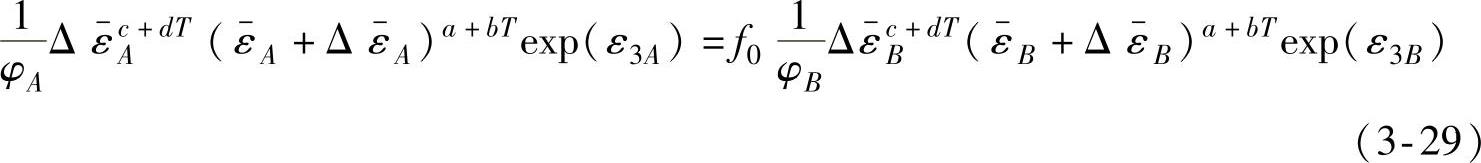
根据功等效原理可得

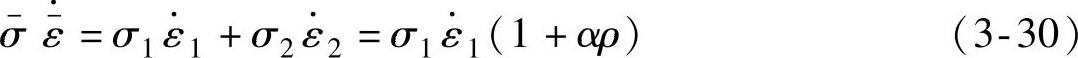
式中，，。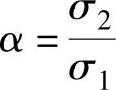

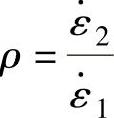令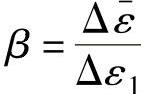，则

因此，式（3-29）可化简为

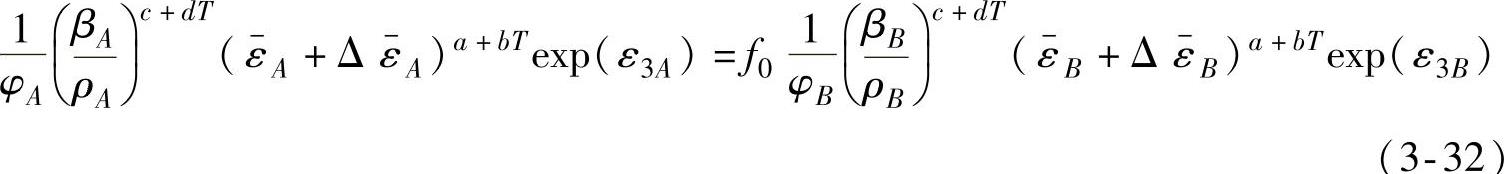
此即超高强度硼钢板右侧成形极限的预测模型。

在式（3-32）中，β为α和ρ的函数，而对于不同的屈服准则，α和ρ之间存在不同的关系，下面对不同屈服准则下α和ρ之间的关系进行了推导。

1）基于Von Mises屈服准则。对于Von Mises屈服准则，其平面应力状态下的表达式为[32]

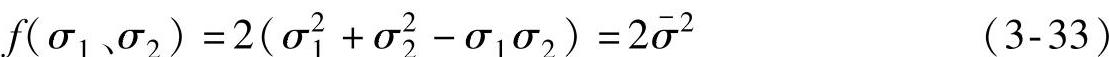
则

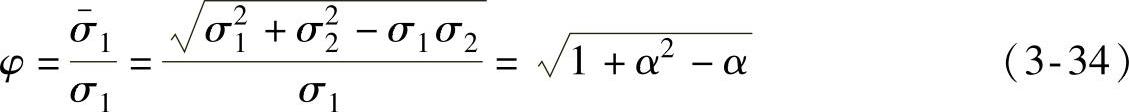
根据材料的流动方程式（3-35）和应力应变关系，可获得α和ρ之间的关系式，见式（3-36）。

式中，。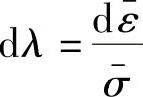

则

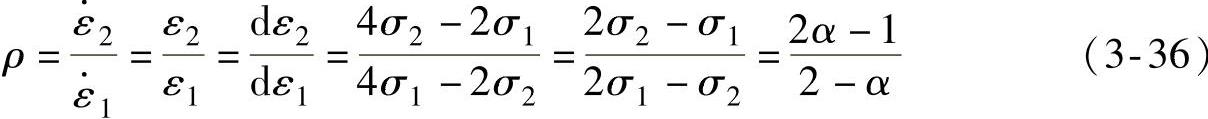
2）基于Hill 48屈服准则。对于Hill 48屈服准则，其平面应力状态下的表达式为[33](www.xing528.com)

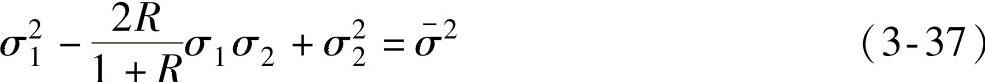
则

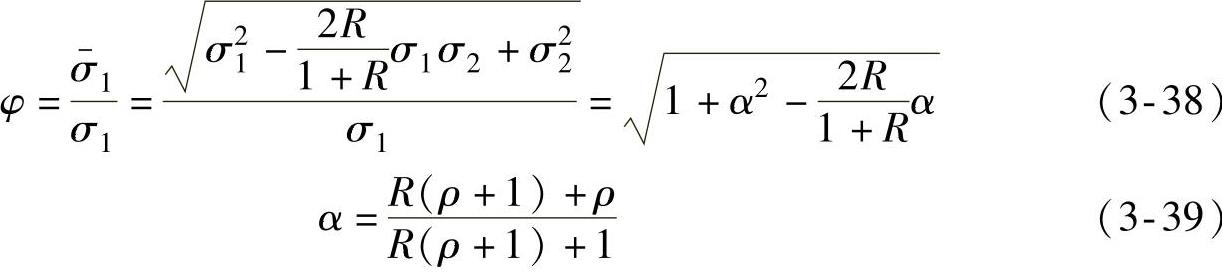
3）基于Logan and Hosford屈服准则。对于Logan and Hosford屈服准则，其平面应力状态下的表达式为[34]

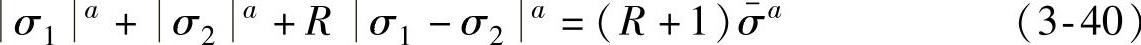
则

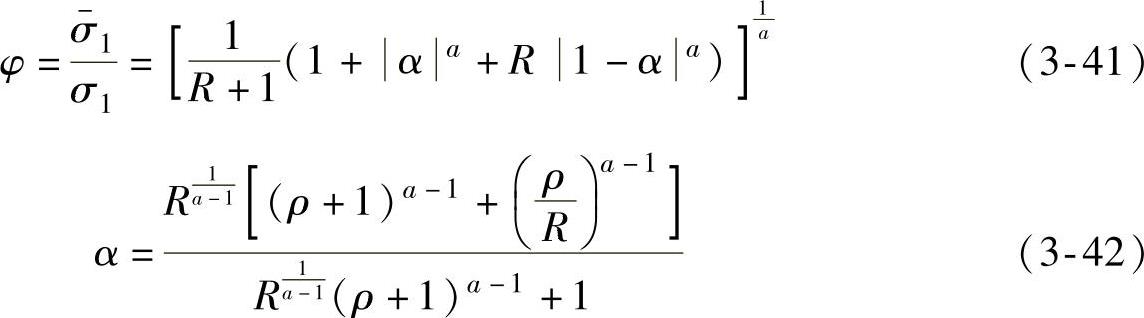
式中，a的取值依赖于材料的晶格类型，对于面心立方晶格材料取6，对于体心立方晶格材料取8～10。3.4.3.2 超高强度硼钢板热成形左侧成形极限的预测模型

对于左侧成形极限的计算，基于Hill集中性失稳模型^[28]来建立预测超高强度硼钢板左侧FLD的修正模型。在该修正模型的计算中，采用了Hill理论模型的应变路径变化趋势，而平面应变处极限的大小为基于M-K理论计算出的应变ε^PS₁。基本推导过程如下。

Hill的集中性失稳条件为

假设材料满足：

（1）屈服函数为

（2）本构关系表达为

两边求导得

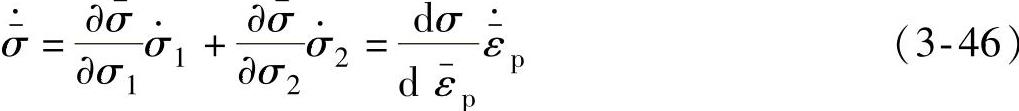
（3）流动准则

一般取σ-p=σ-（σ₁，σ₂）。

对于左侧成形极限的预测，也分别采用Von Mises屈服准则^[32]、Hill 48屈服准则^[33]和Logan and Hosford屈服准则^[34]进行成形极限预测。以下是各屈服准则下的预测模型。

1.基于Von Mises屈服准则

由Von Mises屈服准则及流动准则可得

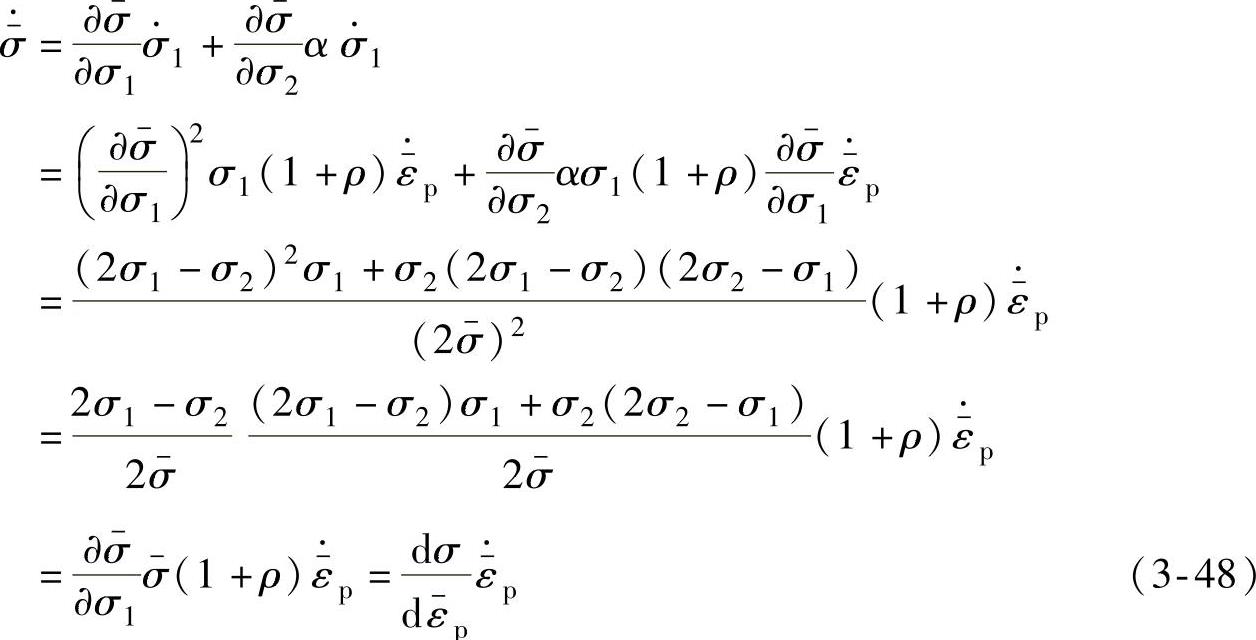
所以，

对于幂指型本构σ=Kε-np，则可化成：

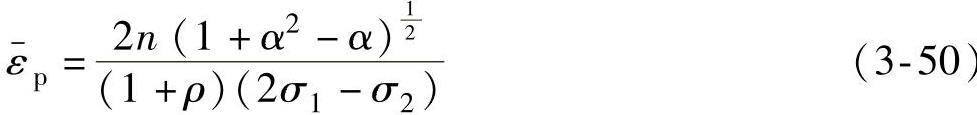
又在线性加载条件下，由流动准则和Von Mises屈服准则可得

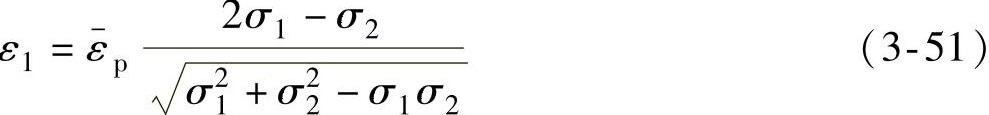
可得

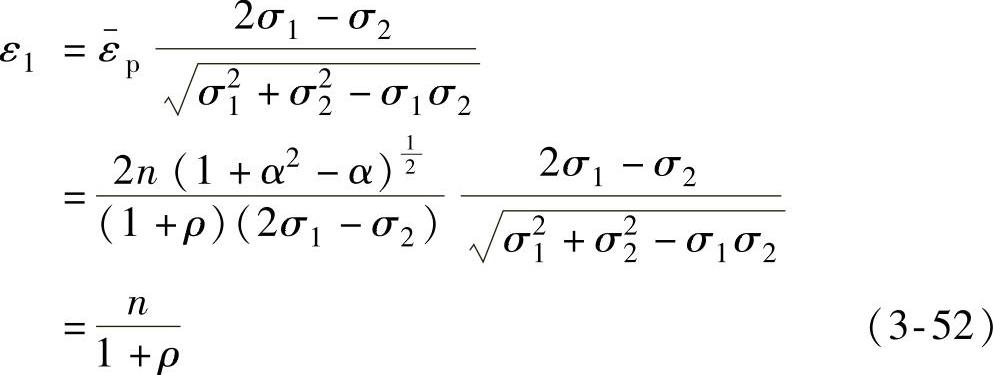
则可得

式中，ρ的取值在-0.5～0之间。

根据上述的预测模型，对应的FLD₀的应变ε₁=n。通过Hill失稳理论预测FLD，曲线位置的高低主要由n值决定。本书基于Hill集中性失稳理论和Von Mi-ses屈服准则，推导出了预测超高强度硼钢板左侧FLD的计算模型，具体形式为

2.基于Hill 48屈服准则

根据同样的方法，应用Hill 48屈服准则所获得的预测超高强度硼钢板左侧FLD的计算模型为

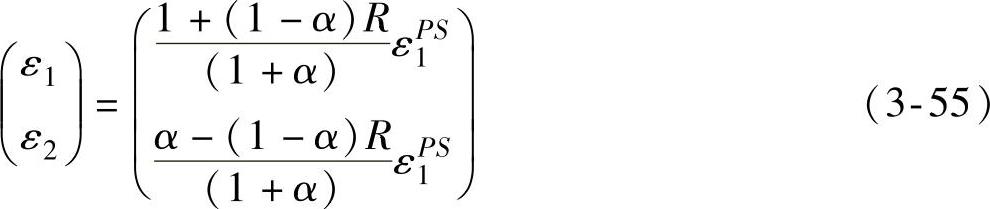
式中，

对于ρ在-0.5～0应变路径下，可以求得左侧的FLD。

3.基于Logan and Hosford屈服准则

根据同样的方法，基于Logan and Hosford屈服准则，所获得的预测超高强度硼钢板左侧FLD的计算模型为

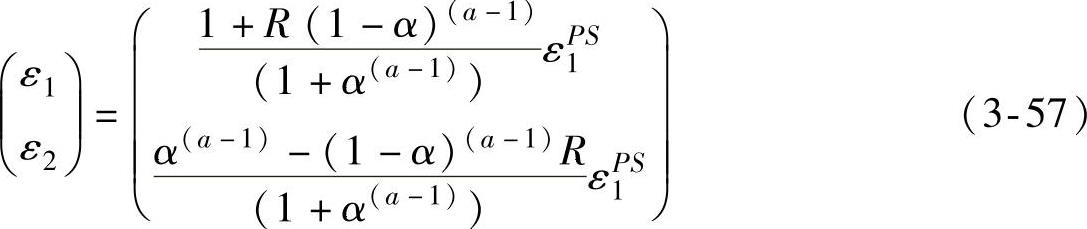
式中，

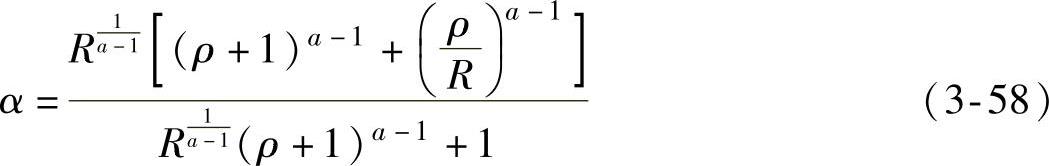
对于ρ在-0.5～0应变路径下，可以求得左侧的FLD。