基于动态回复的本构模型优化方案

硼钢板在高温阶段动态恢复时的变形可理解为硬化机制与软化机制的共同竞争，即位错累积与动态恢复作用的共同竞争。以22MnB5为对象，基于变形机理方面的描述，从位错密度等微观结构入手建立预测精度更高的基于动态回复的本构关系式^[16]。

1）Kocks数学模型。在位错累积与动态恢复作用的共同竞争下，其共同作用结果可用加工硬化率（θ）表示，见式（3-7）：

式中，T是温度；是材料的应变速率。

在T和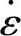为一定值的条件下，θ是σ的函数。根据22MnB5的应力-应变曲线（图3-7）可获得其θ-σ关系曲线，如图3-12所示。

图3-12 θ-σ关系曲线

a） b）T=1173K

由图3-12可知，加工硬化率随着应力的增加而近乎直线下降，当θ接近于0时意味着流动应力达到稳态应力（σ_p），不再继续增加。由于θ与σ几乎呈线性关系，可用Kocks模型^[21]对其进行数值拟合，见式（3-8）：

式中，A和B为材料参数，通过对图3-12中的曲线进行线性拟合即可获得。

对式（3-8）进行积分，并考虑到边界条件，ε=0时，σ=σ₀，可得本构关系式（3-9）：

σ=σ_p-（σ_p-σ₀）exp（-Bε） （3-9）

由于σ_p为稳态应力，即θ=0时的应力，则σ_p可表达为式（3-10）：

σ_p=A/B（3-10）

σ₀为初始屈服应力，可根据试验获得。根据王进等的研究^[22]，σ₀的数学模型可采用式（3-11）来描述：

式中，k₁、n₁为材料常数；Z为Zener-Hollomon参数，其物理意义是温度补偿的应变率因子，可表示为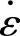和T的函数，见式（3-12）：

式中，Q为形变激活能（kJ/mol）；G为气体常数。由于材料热变形时的流变应力对应变速率及温度的依赖性可以由双曲正弦函数反映^[23]，σ_p又可由Arrhenius方程确定，见式（3-13）：

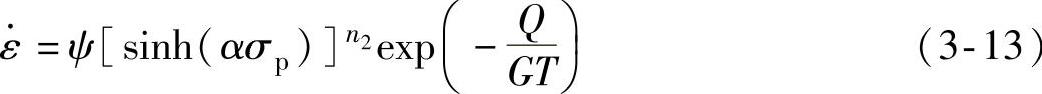
式中，ψ、n₂、α是材料常数。(www.xing528.com)

2）Zener-Hollomon参数的确定。根据式（3-12）和式（3-13），可获得式（3-14）：

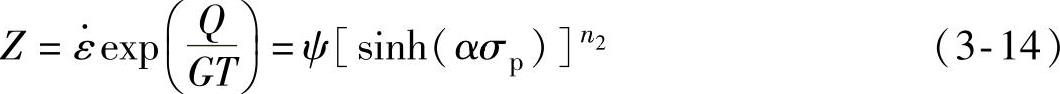
由于式（3-14）中有4个未知量，即ψ、n₂、α和Q，所以不能直接用线性回归来确定这4个未知量的值。先给定α的值，通过对试验数据拟合来确定ψ、n₂、Q的值和误差值，将误差的平方和作为α的函数，通过确定函数的最小值来确定α=0.002^[24]。α的值确定后即可计算ψ、n₂和Q的值。

对式（3-14）求自然对数可得式（3-15）：

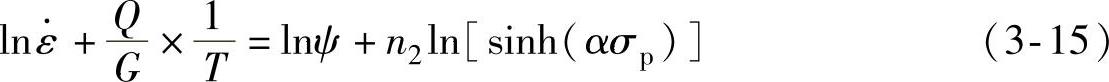
由式（3-15）可得当温度（T）恒定时，有式（3-16）：

而当应变速率（ε·）恒定时，可获得式（3-17）：

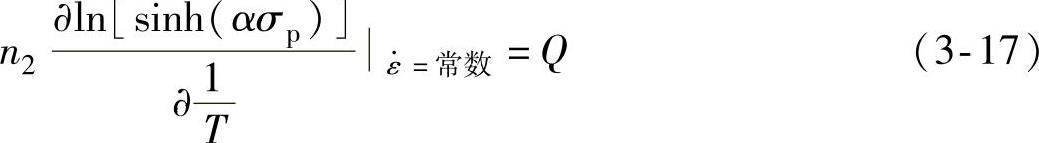
根据式（3-16）和式（3-17），做出不同变形温度下∂ln[sinh（ασ_p）]-lnε·和不同应变速率下∂ln[sinh（ασ_p）]-1/T的关系图，如图3-13及图3-14所示。对图3-13及图3-14中的曲线进行线性拟合可得n₂=6.1798、Q=208.787kJ/mol、ψ=8.3037×10¹¹。

图3-13 不同变形温度下∂ln[sinh（ασ_p）]-lnε关系图

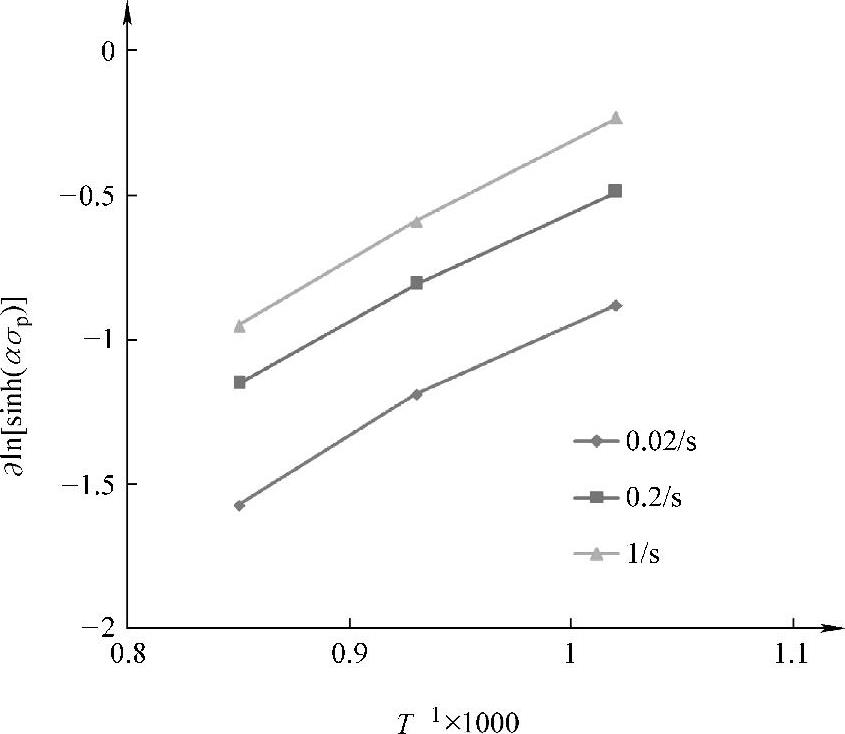
图3-14 不同应变速率下∂ln[sinh（ασ_p）]-1/T的关系图

至此，22MnB5钢板基于动态回复的高温本构关系式即式（3-9）中所有未知参数均已确定，见式（3-18）。根据式（3-18）本构关系式预测的应力-应变曲线与试验曲线比较如图3-15所示，预测精度较高，且更加具有物理意义。

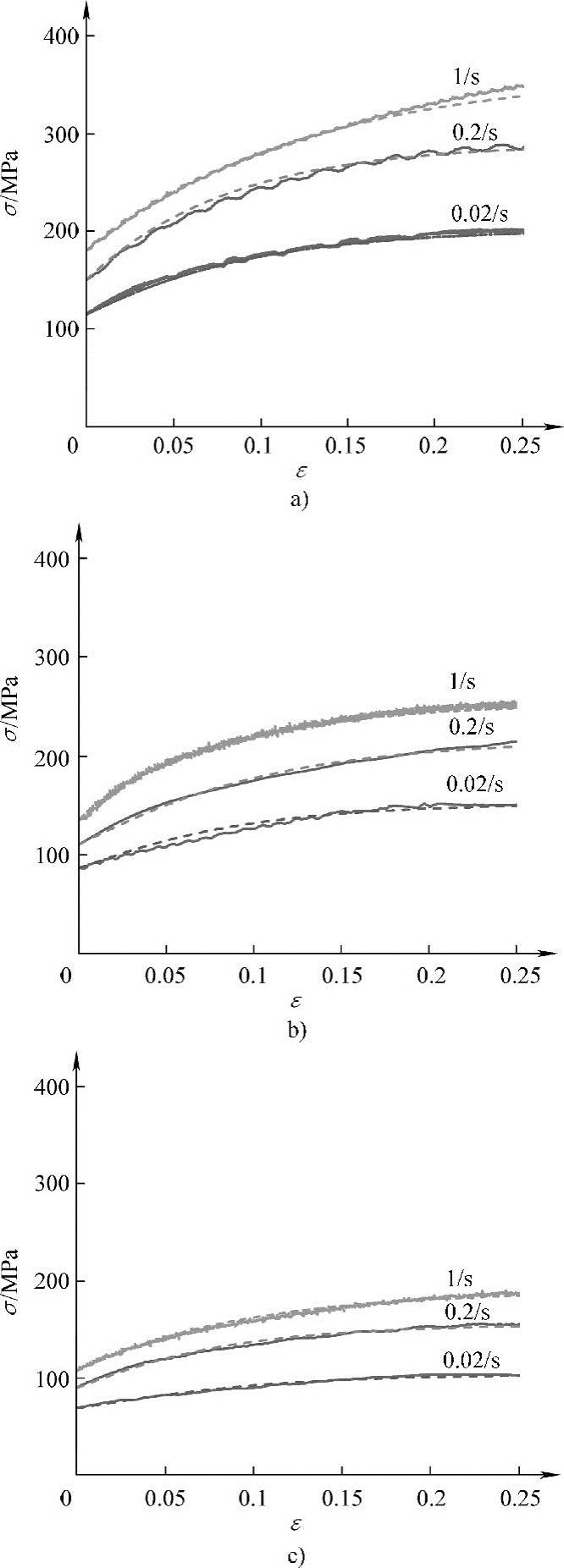
图3-15 试验获得的（实线）与式（3-18）预测的（虚线）高温应力-应变曲线比较

a）T=973K b）T=1073K c）T=1173K

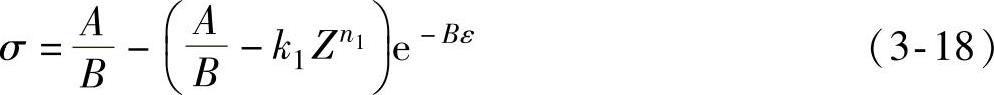
式中，A、B、k₁、n₁为材料常数，根据试验数据拟合得来；Z=ψ[sinh（αA/B）]ⁿ²；其中，ψ=8.3037×10¹¹，α=0.002，n₂=6.1798。