基于井上胜郎模型的本构模型优化研究

由图3-7和图3-8可知，超高强度硼钢板的真实应力-应变曲线属于动态回复型，曲线进入峰值区后其峰值应力随应变的增加而增大，直至进入相对稳定阶段，此阶段动态回复的软化作用与热加工的硬化作用处于动态平衡状态。井上胜郎模型可清楚地反映应力与应变、应变速率及温度之间的变化关系，故以此为模型参考建立硼钢板的本构模型。

1）井上胜郎本构模型。井上胜郎的加工硬化与动态恢复型流变应力数学模型见式（3-1）^[19]：

对上式左右两边取对数，可得式（3-2）：

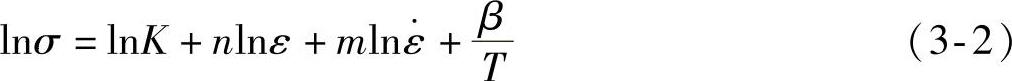
将超高强度硼钢板USIBOR 1500应力应变试验数据代入式（3-2），并用麦夸特法和通用全局优化法进行多元线性回归分析，获得的热冲压流变应力数学模型见式（3-3）：

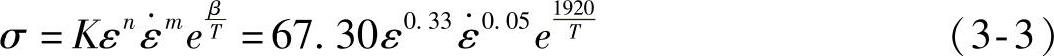
式中，σ为真实应力；ε为真实应变；ε·为应变速率；K为强度系数，也为变形温度的函数；n为硬化指数，也为变形温度及应变速率的函数；m为材料应变速率敏感系数，也为变形温度的函数；T为绝对温度，单位为K；β是与材料有关的常数。

试验结果与拟合曲线对比如图3-9所示。

由图3-9可知，该模型在应变速率不大于0.1/s时与试验结果数据拟合较好，当应变速率超过0.1/s时则产生一定误差。为更好地描述热冲压成形工艺过程中超高强度硼钢板流变应力的变化，将基于井上胜郎模型的流变应力数学模型进行修正。

2）基于温度修正的井上胜郎本构模型。由前面叙述可知，温度是影响超高强度硼钢板真实应力的最大因素。为了获得与实际应力-应变曲线更加吻合的模型，首先对单一温度下的曲线进行拟合，而后分析拟合参数与温度的变化关系，从而获得修正的井上胜郎模型。在井上胜郎模型中，K值和β值是与材料有关的常数，主要考虑温度对n值和m值的影响。

在单一温度下采用井上胜郎模型对873～1173K的材料真实应力-应变曲线进行线性回归分析，可获得不同温度下材料的n值与m值，见表3-3与如图3-10所示。

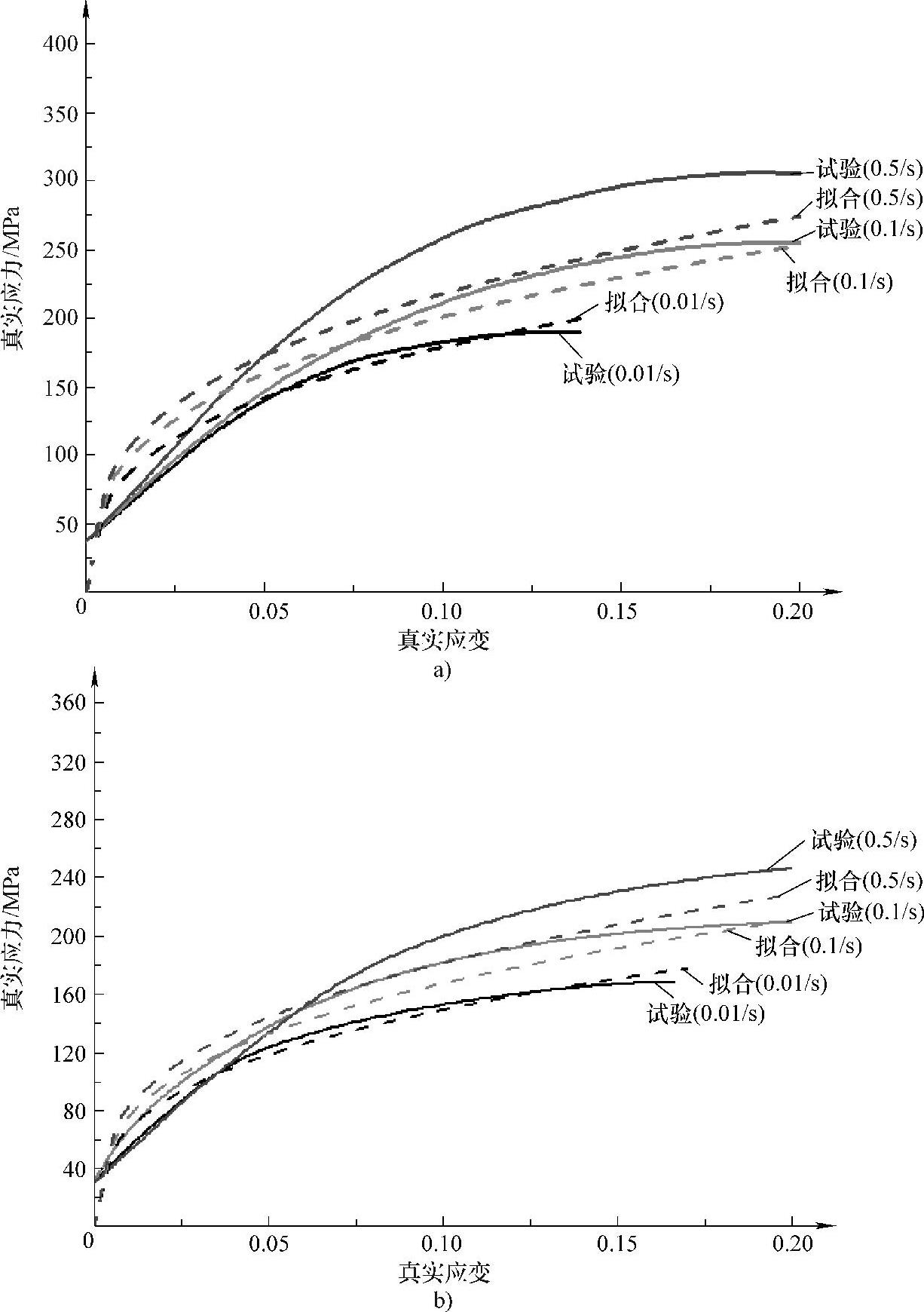
图3-9 试验结果与拟合曲线对比

a）T=973K b）T=1073K

表3-3 不同温度下材料的n值、m值(www.xing528.com)

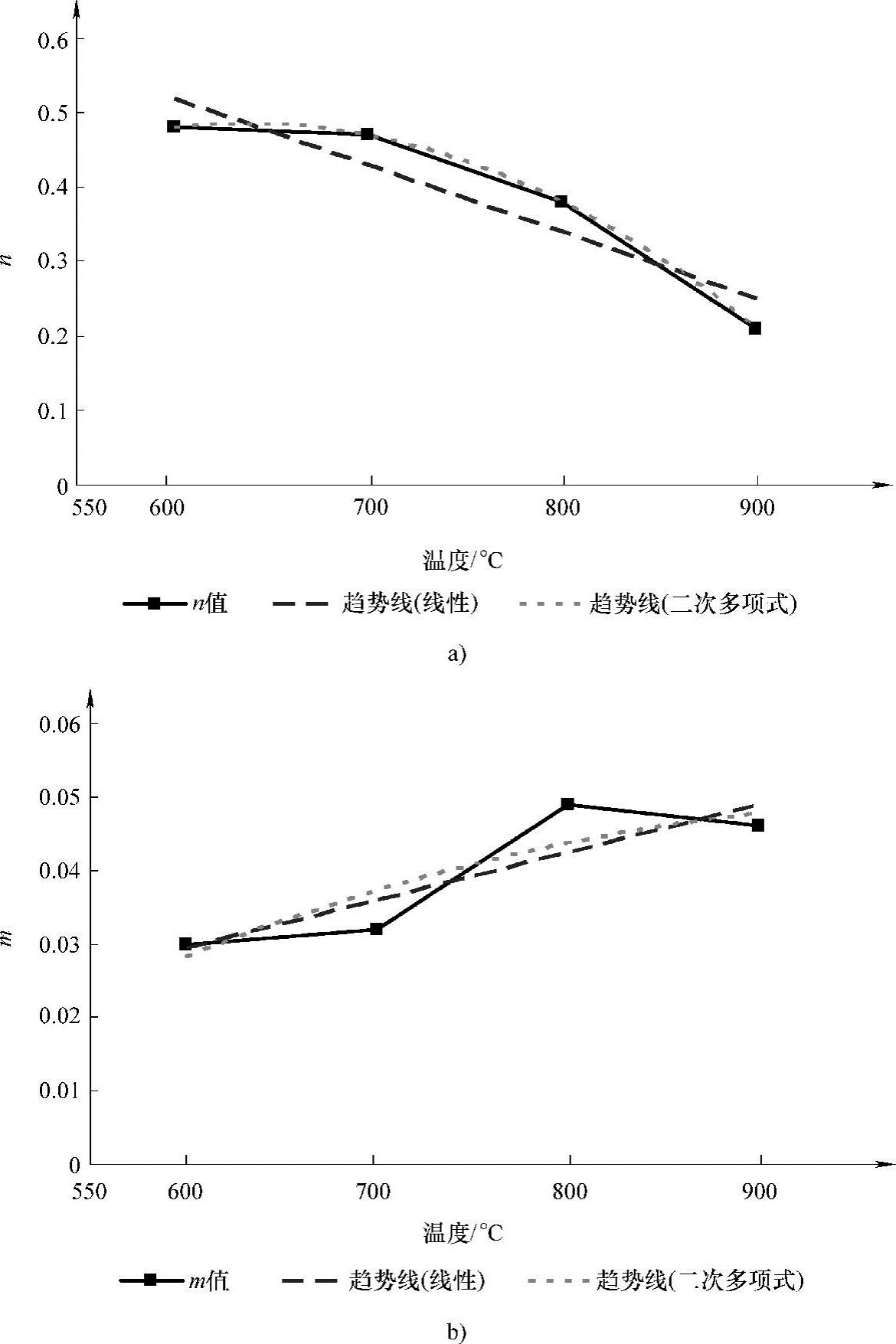
图3-10 温度对n值与m值的影响

a）n值随温度的变化图 b）m值随温度的变化图

由图3-10可知，随着温度的升高，材料的n值逐渐减小，而m值逐渐增大，即温度越高，材料的加工硬化现象越不明显，但对应变速率越敏感。通过添加趋势线对不同温度下的n值与m值变化曲线进行拟合，如图3-10中的虚线所示，可知材料的m值曲线采用线性或二次多项式进行拟合效果相差不大。故本书采用线性函数m=c+dT对原模型中的m值进行修正；而材料的n值曲线采用线性和二次多项式进行拟合有一定差别，分别将n=a+bT与n=a+bT+cT²两种模型代入原本构模型，获得式（3-4）：

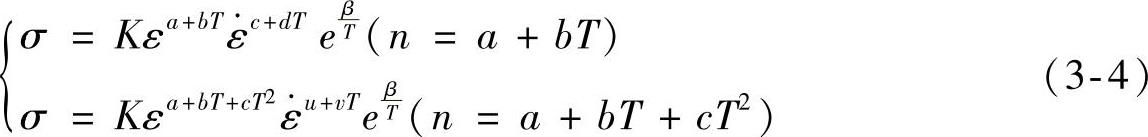
分别采用这两种模型对试验数据进行拟合，两种修正模型的拟合效果相差不大。因此，在保证拟合精度的情况下，为了模型的方便使用，采用线性关系对n值和m值进行修正^[20]。

通过温度对n值和m值的线性修正，获得修正的流变应力数学模型见式（3-5）：

通过试验结果进行多元线性回归分析可得修正后的超高强度硼钢板USIBOR1500的热冲压流变应力数学模型，见式（3-6）。修正后的曲线如图3-11所示。

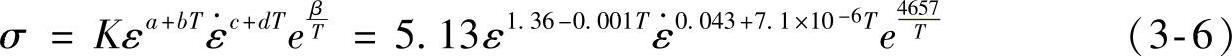
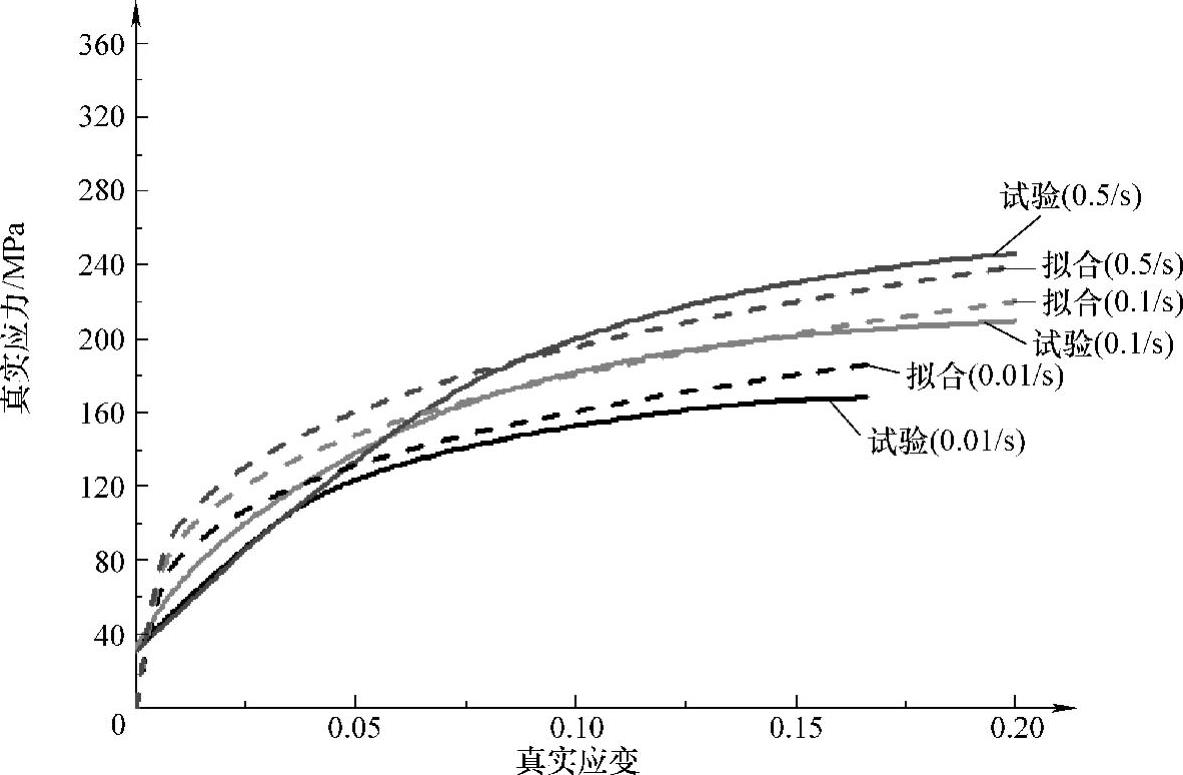
图3-11 修正后的拟合结果（1173K）

可以看出，修正模型比原井上胜郎模型更适于定量描述热冲压成形工艺过程中超高强度硼钢板的流变应力变化，但仍旧存在一定的误差。因此，需要从位错密度等微观结构入手建立预测精度更高的基于动态回复的本构关系式。