密封过程质量控制中的统计学原理应用

在无菌医疗器械屏障系统中吸塑包装成型是一个比较典型的工艺，下面以吸塑包装成型产品的封口强度为例说明理论知识的相关应用。

（1）步骤1：确定控制对象为5 mL注射器吸塑包装成型后的热封强度。

选择控制对象的原则：

①选择技术上最重要的。

②如果指标之间有因果关系，选择因变量。

③控制对象要明确，并为业内广泛理解和接受。

④控制对象必须能以数字来表示。

⑤控制对象要容易测量并容易采取措施改进。

（2）步骤2：取预备数据。

按8 h一个班的封口数据做统计学分析，每隔20 min采集一组样，一共采集25组，每组样采集5个数据，5个数据采集时间间隔应尽量短。

取预备数据的原则：

①至少取25组［根据判稳准则（1）］。

②根据国家规范推荐量，样本量为4或5。

③合理子组原则：组内差异只由偶因造成，组间差异主要由异因造成。前半句的意思是为保证控制图上、下控制界限的间隔距离6σ为最小，从而对异因能及时发出统计信号。在取样本组时应在短间隔内取，避免异因进入。后半句的意思是为了方便发现异因，在过程不稳、变化激烈时应多取样本，而在过程平稳时少取样本。

（3）步骤3：计算Xi、Ri。

Xi是5个数据的平均值，Ri是极差（5个数据中最大值与最小值的差），如表4-15所示。

表4-15　数据与-R图计算表　单位：N/15 mm

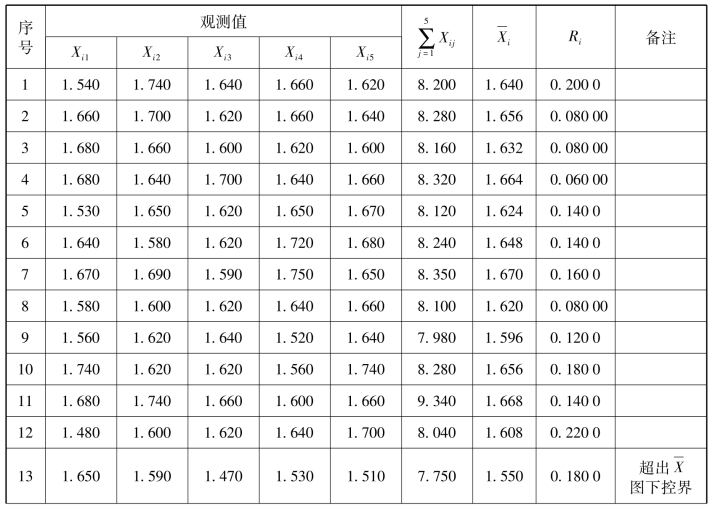
续表

（4）步骤4：计算样本总均值与平均样本极差。

由于，参见表4-15末行，故

（5）步骤5：计算R图控制线并作图。

先计算R图的参数。从表4-15可知，样本大小n=5，则D4=2.114，D3=0，代入R图的公式，得

（6）步骤6：将数据点绘在R图中，判稳。

若稳，则进行步骤7；若不稳，则执行“20字方针”后转入步骤2重新开始。

如图4-25所示，R图可判稳。

图4-25　本例的第一次X-R图

（7）步骤7：建立图。将数据点绘在图中，判稳。

若稳，则进行步骤8；若不稳，则执行“20字方针”后转入步骤2重新开始。

由于n=5，则A2=0.577，再将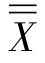=1.633，=0.142 8代入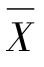图的公式，得

可见，第13组的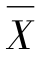值为1.550，小于，故过程的均值失控。经调查其原因后，改进模具，并采取措施防止这种现象再次发生。然后去掉第13组数据，再重新计算R图与图的参数。此时

代入R图与图的公式，得

(www.xing528.com)

由表4-15可见，R图中第17组R=0.300 0出界。于是再次执行“20字方针”后舍去第17组数据，重新计算如下：

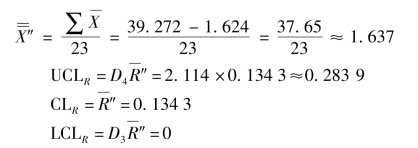
由表4-15可见，R图可判稳。于是计算图如下：

将其余23组样本的极差值与均值分别打点于R图与图上（图4-26），根据判稳准则，可知此时过程的变异度与均值均处于稳态。

图4-26　本例的第二次-R图

（8）步骤8：计算过程能力指数，与规范进行比较。

如果过程能力指数满足技术或规范要求，则转入步骤9。

如果过程能力指数不能满足技术或规范要求，则需要调整过程直至过程能力指数满足技术或规范要求。

假如已经给定规范界为：TL=1.5 N/15 mm，TU=3.0 N/15 mm，现应用全部预备数据作直方图并与规范进行比较，见图4-26。

由图4-26可见，数据的分布与规范界相比较有较多的余量。因此，虽然其平均值并未对准规范界中心，不加以调整问题也不会太大。若加以调整，则还可提高过程能力指数，降低不合格品率，或者也可从技术角度出发考虑适当减小规范界范围。当然，若加以调整则需要重新计算相应的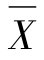-R图。

如果过程的平均值没有偏移，则按以下公式计算：

其中，USL为规范上限，为2.0；LSL为规范下限，为1.5；σ为样本标准差。

方差统计表如表4-16所示。

表4-16　方差统计表

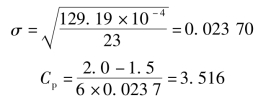
如果过程的平均值是偏移的，则按以下公式计算：

其中，CSL为最近规范极限上限或下限，为2.0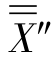；为过程均值，为1.637。

当使用规范极限上限或下限计算出来的Cpk实际应该叫Ppk。Cpk值举例见表4-17。

表4-17　Cpk值举例

（9）步骤9：延长上述图的控制线，对工序进行日常控制。

每日观察，均值偏差≥1.5σ时判异，每日计算σ。

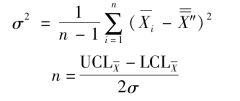
满足下列条件时说明过程能力达到6σ的统计学管理水平：

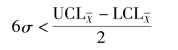
封口强度的规范要求是下限要求，统计学的下限LCL可以大于或等于规范下限LSL（1.5 N/15 mm），但不能小于规范下限。当LCL=LSL时，技术或规范控制稳态和统计稳态重合，这种情况是极难遇到的，必须在满足统计稳态的前提下才能计算Cpk，通过Cpk检查统计稳态满足技术或规范的程度，并最终比较这一程度是否达到可接收水平。

对于不同的n，查图4-27可知产品的不良率。

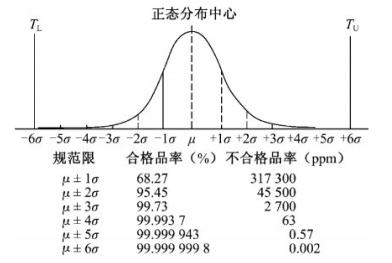
图4-27　正态分布中心与规范中心重合时超出规范限μ±kσ的不合格品率

可以看出，Cpk导出更大的指导意义是PQ的过程，它和SPC是两回事。计算Cpk的上限USL和下限LSL是指规范的上限和下限，规范的上限和下限是根据试验结果人为制定或根据标准制定的。SPC是一定要计算出UCL和LCL的，而SPC过程的上限UCL和下限LCL是由运行的数据按统计学原理计算出来的。当无法确定过程是否进入统计学稳态，在这种情况下计算出来的Cpk也就没有任何指导意义。当计算出UCL和LCL并确认过程进入统计学稳态以后，只要LCL大于或等于LSL且UCL小于或等于USL时，过程一定优于Cpk计算的结果，因此USL和LSL就像高速公路两面的护栏，是绝对不能触碰的，而UCL和LCL则是行车道的白线，这个白线的边缘应小于护栏的宽度。如对小件的环氧乙烷灭菌的技术要求可以制定为大于1.5 N/mm且小于3.0 N/mm，大件的蒸汽灭菌的技术要求可能要制定为大于3.5 N/mm且小于6.5 N/mm等。