密封过程质量控制的统计学原理

（一）无菌医疗器械对无菌保持性提出严格的质量要求

常用的、典型的无菌医疗器械初包装有以下几种形式：

（1）预成型的硬盘和盖材。硬盘通常用热成型或压成型工艺使其预成型。盖材可以是透气的或不透气的。典型的工艺是把密封层将盖材热封于硬盘上。这种带盖的硬盘一般用于外形较大和较重的器械，如外科矫形植入物、心脏起搏器和手术器械包等。

（2）易剥离组合袋。组合袋的典型结构为一面是膜，另一面是膜、纸或非织造布。组合袋常以预成型的形式供应，除留有一个开口（一般是底封）外，其他所有的密封都已形成。保留的开口便于装入器械后进行最终封口。由于组合袋可以加工成各种不同的规格，许多体积小、质量轻的器械都采用组合袋作为无菌屏障系统。

（3）灭菌纸袋。灭菌纸袋用医用级多孔纸制成，折成一个长的无折边或有折边的管袋状（平面的或立体的）。管袋在其长度方向上用双线涂胶密封，然后切成所需规格，一端用一层或多层黏合剂密封，多次折叠也可用于提高闭合强度。开口端通常有一个错边或一个拇指切，以便于打开。纸袋的最终闭合在灭菌前形成。

（4）顶头袋。顶头袋主要由两个不透气但相容的膜面组成，一个膜面通常比另一面短几英寸并热封有涂胶的透气材料。透气材料用来在最终使用时剥开袋体。顶头袋主要用来包装较_大体积的器械，如器械包等。

（5）成型-装入-密封（FFS）的包装过程。这种FFS过程中生产出来的无菌屏障系统，其形式有组合袋式、带盖硬盘式或有一个已吸塑成型的软底模。在FSS过程中，上下包装部分放入FFS机器中，包装机器对下部分包装进行成型，装入器械，盖上包装面材后密封形成无菌屏障系统。

（6）四边密封（4SS）过程包装。4SS是像流水包装一样的不间断的包装过程。最为常见的是使用一种旋转密封设备来形成密封。在4SS过程中，下包装部分和上包装部分放在4SS包装机器上，产品放在下包装部分，再将上包装面材放在产品上，最后进行四边密封。如手套和创面敷料的包装便是采用4SS的包装形式。

以上列出的无菌屏障系统未包含全部的包装形式，但无论采用哪种包装形式，确保产品的无菌性能最关键的是密封过程的质量问题。为使无菌屏障系统能够保持产品灭菌的有效性（10-6）和包装的完整性，保证产品安全有效，从现代质量管理技术的应用来讲，运用过程能力分析方法和六西格玛管理方法无疑是可靠性较高的一种控制模式。

所谓过程能力也称为工序能力，是衡量过程加工质量内在的一致性、最稳状态下的最小波动性的有效分析方法。当过程处于稳定状态时，产品的质量特性值有99.73%散布在区间［μ-3σ，μ+3σ］（其中，μ为产品特性值的总体均值，σ为产品特性值总体标准差），即几乎全部产品特性值都落在±3σ的范围内，这样就达到了一般生产质量的要求。

“σ”是希腊字母，在统计学上用来表示标准偏差值，用以描述总体中的个体离均值的偏离程度。测量出的σ表征诸如单位缺陷、百万缺陷或错误的概率性，σ值越小，缺陷或错误就越少。6σ质量水平意味着在所有的过程和结果中，99.999 66%是无缺陷的，也就是说，做100万件事情，其中只有3.4件是有缺陷的。σ越小，过程的波动越小，过程以最低的成本损失、最短的时间周期满足顾客要求的能力就越强。大多数企业在3σ～4σ间运转，也就是说每百万产品失败数在6 210～66 800之间，这个失败的概率对于无菌医疗器械的无菌保持性而言是远远不够的。

近年来，由于科学技术的发展，产品的不合格品率迅速降低，如电子产品的不合格品率由过去的百分之一、千分之一降到百万分之一（ppm，parts per million，10-6）乃至十亿分之一（ppb，parts per billion，10-9），生产控制方式由过去的3σ控制方式演进为6σ控制方式。3σ控制方式的过程均值无偏移不合格品率为2.7×10-3，过程均值偏移1.5σ的不合格品率为66 807 ppm。限于当前的科技水平，由种种因素造成过程的实际漂移大约为1.5σ。6σ控制方式的过程均值无偏移不合格品率为0.002×10-6=2.0×10-9，过程均值偏移1.5σ的不合格品率为3.4 ppm（图4-4）。故将6σ控制方式与3σ控制方式相比较，在均值无偏移条件下不合格品率降低了2.7×10-3/（2.0×10-9）=1.35×106，即135万倍！在均值偏移1.5σ的条件下不合格品率也降低了66 807/3.4=19 649.12≈20 000，即2万倍！可称之为超严格质量要求。各种产品都有相应的超严格质量要求。例如，冰箱与空调的重要部件压缩机不合格品率的国际水平为200 ppm，无菌产品的阳性率为1×10-6，如果还用传统的3σ的过程控制方法显然不合适。另外，密封质量的检测均为破坏性检测，而且检测单元一般只有1.5 cm，1.5 cm的不合格足以导致整个产品的不合格。因此，不可能利用抽样原则进行一般的检测作为密封质量的控制手段，通常把这样的过程称为“特殊过程”。由于“特殊过程”的质量情况在加工完成后无法通过正常的抽样检验完成，所以“特殊过程”的质量控制一定要采取SPC。

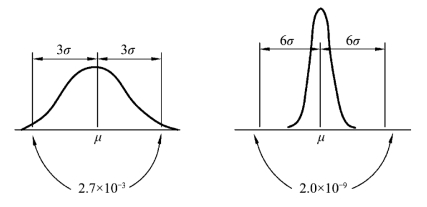
图4-4　3σ控制方式与6σ控制方式的比较

无菌医疗器械产品要想在国际市场上立于不败之地，无菌的属性要求就要满足超严格质量要求，就需要采用先进的科学技术与先进的管理科学。一般说来，先进的科学技术可以提高产品质量指标的绝对值，而先进的管理科学则可以在现有的条件下将其质量波动控制到最小。

（二）统计过程控制（SPC）的基本概念

做好质量管理应明确下列两点：

（1）贯彻预防为主的原则，这是现代质量管理的核心与精髓。

（2）对于质量管理所提出的原则、方针、目标要有科学的措施与方法来保证它们的实现。这是质量管理科学一个十分重要的特点，充分体现了质量管理的科学性。

上述第（1）点在ISO 13485标准中已有充分的反映。但上述第（2）点则非广为人知，缺乏这方面系统的科学知识，这也是造成目前质量体系管理中形式主义泛滥的根源之一。

1.SPC的含义

SPC是英文Statistical Process Control（统计过程控制）的简称。所谓SPC，是指为了贯彻预防为主的原则，应用统计技术对过程的各个阶段进行评估和监察，从而保证产品与服务满足要求的均匀性。

统计技术虽然涉及数理统计的许多分支，但SPC中的主要工具是控制图理论。因此，推行SPC必须对控制图有较为深入的了解，否则就不可能通过SPC取得真正的实践。

2.SPC的特点

（1）与质量体系管理相同，强调全员参加，而不是只依靠少数质量管理人员。

（2）强调应用统计方法来保证预防原则的实现。

（3）SPC不是用来解决个别工序采用什么控制图的问题，而是强调从整个过程、整个体系出发来解决问题。SPC的重点就在于“P（Process，过程）”。

3.SPC的发展

SPC可以判断过程的异常，及时告警，但SPC也有其局限性，它不能告知异常由什么因素引起，发生于何处，即不能进行诊断。而现场迫切需要解决诊断问题，否则即使想纠正异常也无从下手。故现场与理论都迫切需要将SPC发展为SPD（Statistical Process Diagnosis，统计过程诊断）。

SPD不但具有SPC及时告警进行控制的功能，而且具有SPC所没有的诊断功能，故SPD是SPC进一步发展的新阶段。SPD就是利用统计技术对过程中的各个阶段进行监控与诊断，从而达到缩短诊断异常的时间，以便迅速采取纠正措施，减少损失、降低成本，保证产品质量的目的。SPD是20世纪80年代发展起来的。

（三）控制图的结构

控制图（Control Chart）是对过程质量特性值进行测定、记录、评估，从而监察过程是否处于受控状态的一种用统计方法设计的图。控制图上有中心线（CL，Central Line）、上控制限（UCL，Upper Control Limit）和下控制限（LCL，Lower Control Limit），并有按时间顺序抽取的样本统计量数值的描点序列，见图4-5。UCL、CL与LCL统称为控制线（Control Line）。若控制图中的描点落在UCL与LCL之外或描点在UCL与LCL之间的排列不随机，则表明过程异常。控制图有一个很大的优点，即在图中将所描绘的点与控制界限或规范界限相比较，从而能够直观地看到产品或服务的质量。

图4-5　控制图示例

控制图是贯彻预防原则的SPC与SPD的重要工具。控制图可用以直接控制与诊断过程，故为质量管理七个工具的核心。常用的质量管理七个工具分别为因果图（Causeeffect Diagram）、排列图（Pareto Diagram）、直方图（Histogram）、散布图（Scatter Diagram）、控制图（Control Chart）、分层法（Stratification）、检查表（Check List）。

（四）产品质量的统计观点

产品质量的统计观点是现代质量管理的基本观点之一，产品质量的统计观点包含下列内容：

1.产品的质量具有变异性

产品质量具有一定的变异性这是众所周知的事实，但在工业革命以后，人们一开始误认为现在由机器来进行生产，生产的产品应该是一致的。经过多年的实践，随着测量理论与测量工具的进步，人类才终于认识到尽管是机器生产，还是会造成产品质量的不一致。

2.产品质量的变异具有统计规律

产品质量的变异也是有规律性的，但它不是通常的确定性现象的确定性规律，而是随机现象的统计规律。

所谓确定性现象，就是在一定条件下，必然发生或不可能发生的事件。但在质量方面，我们经常遇到的却是随机现象，即在一定条件下事件可能发生也可能不发生。如我们无法预知电灯泡的寿命一定是1 000 h，但是在大量的统计数据的基础上我们可以说电灯泡的寿命有80%的可能大于1 000 h，这就是对随机现象的一种科学的描述。

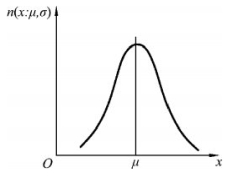
图4-6　正态分布密度

对于随机现象，通常用分布（Distribution）来描述，分布可以告诉我们变异的幅度有多大，出现这么大幅度的可能性（概率，Probability）就有多大，这就是统计规律。对于计量特性值，如长度、质量、时间、强度、纯度、成分、收率等连续性数据，最常见的是正态分布（Normal Distribution），见图4-6。对于计件特性值，如特性测量的结果只有合格与不合格两种情形的离散性数据，最常见的是二项分布（Binomial Distribution），见图4-7。对于计点特性值，如铸件的沙眼数、布匹上的疵点数、电视机中的焊接不合格数等离散性数据，最常见的是泊松分布（Poisson Distribution），见图4-8。计件值与计点值又统称计数值，都是可以0个，1个，2个……这样数下去的数据。掌握这些数据的统计规律可以保证和提高产品质量。

图4-7　二项分布（p为不合格品率）

图4-8　泊松分布（λ为单位缺陷数）

（五）控制图原理

1.正态分布的基础知识

数据越多，分组越密，则直方图越趋近一条光滑曲线，如图4-9所示。连续值最常见的分布为正态分布，其特点为中间高、两头低、左右对称并延伸到无穷。

正态分布是一条曲线，一般采用两个参数来表示，即平均值（μ）和标准差（σ）。平均值（μ）与标准差（σ）的变化对于正态分布曲线的影响分别参见图4-10与图4-11所示。由图4-11可见，标准差（σ）越大，则加工质量特性值越分散。要关注标准差（σ）与质量有着密切的关系。

图4-9　直方图趋近光滑曲线

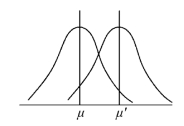
图4-10　正态曲线随着平均值（μ）变化

图4-11　正态曲线随着标准差（σ）变化

正态分布的两个参数平均值（μ）与标准差（σ）是互相独立的。事实上，不论平均值（μ）如何变化，都不会改变正态分布的形状，即标准差（σ）；反之，不论正态分布的形状即标准差（σ）如何变化，也不会影响数据的对称中心，即平均值（μ）。

正态分布有一个事实在质量管理中经常用到，即不论μ与σ取值为何，产品质量特性值落在［μ-3σ，μ+3σ］范围内的概率为99.73%，这是数学计算的精确值，见图4-12。于是产品质量特性值落在［μ-3σ，μ+3σ］范围外的概率为1-99.73%=0.27%，而落在大于μ+3σ一侧的概率为0.27%/2=0.135%≈1‰。

控制图的形成：首先把图4-12按顺时针方向转90°，如图4-13（a）所示。由于图中数值上小、下大不符合常规，故再将图4-13（a）上下翻转180°，成为图4-13（b），这样就得到了一张控制图，具体说是单值（X）控制图，参见图4-14。图4-14中的UCL=μ+3σ为上控制限，CL=μ为中心线，LCL=μ-3σ为下控制限。

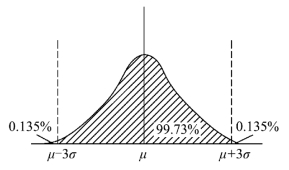
图4-12　正态分布曲线下的面积

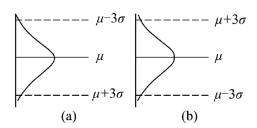
图4-13　控制图的演变

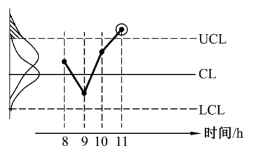
图4-14　X控制图

2.控制图原理的第一种解释

控制纸塑袋密封的质量，每隔1 h随机抽取一个1.5 cm长的纸塑封口样品，测量其剥离强度，在图4-14上描点，并用直线段将点连接，以便观察点的变化趋势。由图4-14可看出，前3个点都在控制限内，但第4个点却超出了UCL。为了醒目，把第4个点用小圆圈圈起来，表示第4个样品的剥离强度过大了，应引起注意。现在对这第4个点应做出什么判断呢？摆在我们面前的有两种可能性：

（1）若过程正常，即分布不变，则点超过UCL的概率只有1‰左右。

（2）若过程异常，如设异常原因为磨具上有异物，则随着热封的进行，加工的封口强度将逐渐变大，μ逐渐增大，于是分布曲线上移，点超过UCL的概率将大为增加，可能为1‰的几十乃至几百倍。

现在第4个点已经超出UCL，那么应为上述两种情形中的哪一种呢？由于情形（2）发生的可能性要比情形（1）大几十乃至几百倍，故我们认为上述异常是由情形（2）造成的。由此可得出结论：点出界就判异！

用数学语言来说，这就是小概率事件原理。小概率事件实际上不发生，若发生即判断异常。控制图就是统计假设检验的图上作业法。在控制图上每描一个点就是做一次统计假设检验。

3.控制图原理的第二种解释

现在换个角度再来研究一下控制图原理。根据来源的不同，质量因素可分为人、机、料、法、环、测6个方面。但从对产品质量的影响大小来分，质量因素可分为偶然因素（简称偶因）与异常因素（简称异因，也称为可查明因素或系统因素）两类。偶因是过程固有的，始终存在，对质量的影响微小，但难以除去，如制袋机开动时的轻微振动等。异因则非过程固有，有时存在，有时不存在，对质量影响较大，但不难除去，如磨具或垫圈磨损等。

偶因引起质量的偶然波动（简称偶波），异因引起质量的异常波动（简称异波）。偶波是不可避免的，但对质量的影响微小，故可把它看作背景噪声而听之任之。异波则不然，它对质量的影响较大，且采取措施不难消除，故在过程中异波及造成异波的异因是关注的重点，一旦发生，就要尽快采取措施加以消除，并纳入标准规范，保证不再出现。

偶波与异波都是产品质量的波动，如何发现异波？可以这样设想：假定在过程中，异波已经消除，只剩下偶波，这当然是最小波动。根据这个最小波动，应用统计学原理设计控制图相应的控制界限。当异波发生时，点就会落在界外，若点频频出界就表明存在异波。控制图上的控制界限就是区分偶波与异波的科学界限。

综上所述，控制图的实质是区分偶然因素与异常因素，要把质量波动区分为偶波与异波两类并分别采取不同的对待策略。

（六）控制图在贯彻预防原则中的作用

对于控制图在贯彻预防为主的原则中的作用可以按下述情形分别讨论：

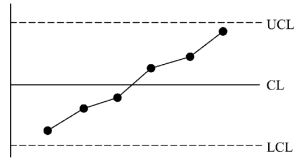
图4-15　控制图点子形成倾向

（1）应用控制图对生产过程进行监控，如出现如图4-15所示的上升倾向，则显然过程有问题，故异因刚一露头，即可发现，并可以及时采取措施加以消除，这当然是预防，但现场较少出现这种情形。

（2）较常出现的是控制图上点突然出界，显示异常。这时必须按照“20字方针”去做，即“查出异因，采取措施，加以消除，不再出现，纳入标准”。每执行一次这“20字方针”，就消灭一个异因，于是对此异因而言，就起到了预防作用。不按这“20字方针”执行，控制图就形同虚设。

控制图的作用是及时报警，但只在控制图上描点是不可能起到预防作用的。因此，要求现场第一线的工程技术人员推行SPC与SPD，把执行上述“20字方针”作为日常工作的一部分。

（七）稳态

（1）所有的控制都有一个标准作为基准，若过程不处于此基准的状态，则必须立即采取措施，将其恢复到此基准。统计过程控制（SPC）当然也采取一种标准（统计标准）作为其基准，这就是统计控制状态或稳态。

（2）统计控制状态简称控制状态，是指过程中只有偶因而无异因产生的变异状态。

（3）控制状态是生产追求的目标，因为在控制状态下有下列几大好处：

①对产品质量有完全的把握。通常，控制图的控制界限都在规范界限之内，故至少有99.73%的产品是合格品。

②生产也是最经济的。偶因和异因都可能造成不合格品，由偶因造成的不合格品极少，只有2.7‰，不合格品主要是由异因造成的。故在受控制状态下所生产的不合格品最少。

③在控制状态下，过程的变异最小。

（4）推行SPC能够保证实现全过程的预防。一道工序达到受控状态称为稳定工序，每道工序都达到受控状态称为全稳生产线。SPC之所以能够保证实现全过程的预防，依靠的就是全稳生产线。

（八）两种错误

控制图对过程的监察是通过抽查来进行的，但抽查就不可能不存在差错。控制图通常会出现两种错误：

1.第一种错误：虚发警报（False Alarm）

图4-16　控制图的两种错误

生产正常而点偶然超出界外，根据点出界就判异，于是就犯了第一种错误。通常犯第一种错误的概率记以α，见图4-16。第一种错误将造成寻找根本不存在的异因的损失。(www.xing528.com)

2.第二种错误：漏发警报（Alarm Missing）

过程已经异常，但仍会有部分产品其质量特性值的数值大小偶然位于控制界限内。如果抽取到这样的产品，点就会在界内，从而犯了第二种错误，即漏发警报。通常犯第二种错误的概率记以β，见图4-16。第二种错误将造成废次品增加的损失。

3.如何减少两种错误所造成的损失

控制图共有三条线，一般正态分布的CL居中不动，UCL与LCL互相平行，故只能改动UCL与LCL二者之间的间隔距离。从图4-16可见，若此间隔距离增加，则α减小，β增大；反之则相反。故无论如何调整上下控制限的间隔，两种错误都是不可避免的。

解决办法是：根据使两种错误造成的总损失最小这一点来确定UCL与LCL二者之间的最优间隔距离。经验证明休哈特所提出的3σ方式较好，在不少情况下，3σ方式都接近最优间隔距离。

（九）3σ方式

3σ方式的公式如下：

UCL=μ+3σ

CL=μ

LCL=μ-3σ

式中，μ、σ为统计量的总体参数。

这是休哈特控制图的总公式，真正应用时需要经过下列两个步骤：

（1）具体化。

（2）对总体参数进行估计。

要注意总体参数与样本参数不能混为一谈。总体包括过去已制成的产品、现在正在制造的产品以及未来将要制造的产品的全体，而样本只是过去已制成产品的一部分。故总体参数的数值是不可能精确知道的，只能通过已知的数据加以估计，而样本参数的数值则是已知的。

还必须注意，规范界限不能用作控制界限。规范界限用以区分合格与不合格，控制界限则用以区分偶波与异波，二者完全是两码事，不能混为一谈。

（十）常用的休哈特控制图

常用的休哈特控制图如表4-13所示（GB/T 4091）。分析表4-13可知，实质上只有四种控制图：图、X-Rs图、npT图、cT图。

表4-13　常规控制图

（十一）分析用控制图与控制用控制图

一道工序开始应用控制图时，几乎总不会恰巧处于稳态，即总是存在异因。如果以这种非稳态状态下的参数来建立控制图，控制图界限之间的间隔一定较宽，以这样的控制图来控制未来，将会导致错误的结论。因此，开始时需要将非稳态的过程调整到稳态，这就是分析用控制图的阶段。等到过程调整到稳态后，才能延长控制图的控制线作为控制用控制图，这就是控制用控制图的阶段。根据使用目的的不同，控制图可分为分析用控制图与控制用控制图。

1.分析用控制图

分析用控制图主要用于分析以下两点：

（1）所分析的过程是否为统计控制状态。

（2）该过程的过程能力指数（Process Capability Index）是否满足要求。

荷兰学者维尔达（S.L.Wievda）把过程能力指数满足要求称为技术稳态（State in Technical Control）。

由于Cp值必须在稳态下计算，故必须先将过程调整到统计稳态，然后再调整到技术控制状态。

根据统计控制状态与技术控制状态是否达到可以分为如表4-14所示的四种情况：

（1）状态Ⅰ：统计控制状态与技术控制状态同时达到，最理想。

（2）状态Ⅱ：统计控制状态未达到，技术控制状态达到。

（3）状态Ⅲ：统计控制状态达到，技术控制状态未达到。

（4）状态Ⅳ：统计控制状态与技术控制状态均未达到，最不理想。

表4-14　控制图状态分类

由表4-14可见，从状态Ⅳ达到状态Ⅰ的途径有两个：状态Ⅳ⇒状态Ⅱ⇒状态Ⅰ，或状态Ⅳ⇒状态Ⅲ⇒状态Ⅰ。究竟通过哪条途径应由具体的技术经济分析来决定。虽然从计算Cp值上讲，应该先达到状态Ⅲ，但有时为了更加经济，保持在状态Ⅱ也是有的。当然，在生产线的末道工序一般以保持状态Ⅰ为宜。显然，状态Ⅳ最不理想，也是现场所不能容忍的，需要加以调整，使之逐步达到状态Ⅰ。分析用控制图的调整过程即质量不断改进的过程。

2.控制用控制图

当过程达到所确定的状态后，才能将分析用控制图的控制线延长作为控制用控制图。由于后者相当于生产中的立法，故由前者转为后者时应有正式交接手续。这里要用到判断稳态的准则（简称判稳准则），在稳定之前还要用到判断异常的准则（简称判异准则）。

在日常管理中，关键是保持所确定的状态。若经过一个阶段后可能又出现异常，这时应按照前面提到的“20字方针”去做调整，使之恢复到所确定的状态。

（十二）休哈特控制图的设计思想

休哈特控制图的设计思想是先定α，再看β。

（1）按照3α方式确定UCL、CL、LCL，就等于确定α0=0.27%。

（2）通常的统计一般采用α=1%，5%，10%三级。但休哈特为了增加使用者的信心，把休图的α取得特别小（α取为零是不可能的，事实上若α取零，则UCL与LCL之间的间隔将为无穷大，从而β为1，必然漏报），这样β就大，需要增加第二类判异准则，即界内点排列不随机判异。

（十三）判稳准则

1.判稳准则的思路

对于判异来说，“点出界就判异”虽不是百发百中，也是千发九百九十七中，相对可靠。但在控制图上如一个点未出界，可否判稳？正常情况下一个点未出界有两种可能：一是过程稳定，二是漏报（这里由于α小，所以β大）。故一个点未出界不能立即判稳。但若连续m（m1）个点都未出界，则情况就大不相同，这时整个点系列的β总=βm要比个别点的β小很多，可以忽略不计。于是只剩下一种可能，即过程稳定。如果连续在控制界内的点更多，则即使有个别点偶然出界，过程仍可看作是稳态的。上述就是判稳准则的思路。

2.判稳准则的内容

在点随机排列的情况下，符合下列情况之一即可判稳：

（1）连续25个点，界外点数d=0。

（2）连续35个点，界外点数d≤1。

（3）连续100个点，界外点数d≤2。

3.分析上述判稳准则的α

判稳准则也是对随机现象加以判定，故也可能发生两种错误。以上述判稳准则（2）为例分析该准则的α，即α2。

设过程正常，则

上式表示，在过程正常的情况下，连续35点出现d＞1是小概率事件，实际上不发生，若发生即判断过程不稳（失控）。α2就是执行第（2）条判稳准则犯第一种错误的概率，也称为显著性水平。类似情况下可求出α1与α3。

于是有α1=0.065 4，α2=0.004 1，α3=0.002 6。

由于α1要比α2、α3大得多，有的专家认为，应将第一条判稳准则舍去，但GB/T 4091标准并未这样要求，这显然是考虑了经济因素的缘故。

（十四）判异准则

判异准则有两类：①点出界就判异；②界内点排列不随机判异。

由于点的数目未加限制，故后者的模式原则上可以有无穷多种，但现场保留下来继续使用的只有具有明显物料意义的若干种，在控制图的判断中要注意对这些模式加以识别。

GB/T 4091标准规定了常规控制图的8种判异准则：

准则1：1个点落在A区以外（图4-17）。

在许多应用中，准则1甚至是唯一的判异准则。准则1可对参数μ的变化或参数σ的变化给出信号，变化越大，则给出信号越快。准则1还可以对过程中的单个失控做出反应，如计算错误、测量误差、原材料不合格、设备故障等。准则1犯第一种错误的概率（或称显著性水平）记为α0=0.002 7。

准则2：连续9个点落在中心线同一侧（图4-18）。

此准则是为了补充准则1而设计的，以改进控制图的灵敏度。选择9个点是为了使其犯第一种错误的概率α与准则1的α0=0.002 7大体相仿。出现如图4-18所示准则2的现象，主要是分布的μ减小的缘故。

图4-17　准则1的图示

图4-18　准则2的图示

准则3：连续6个点递增或递减（图4-19）。

此准则是针对过程平均值的趋势进行设计的，它判定过程平均值的较小趋势要比准则2更为灵敏。产生趋势的原因可能是工具逐渐磨损、维修逐渐变坏、操作人员技能逐渐提高等，从而使得参数α随着时间而变化。

准则4：连续14个点中相邻点上下交替（图4-20）。

出现这种现象是由于轮流使用两台设备或由两位人员轮流进行操作而引起的系统效应。实际上这是存在一个数据分层不够的问题。选择14个点是通过统计模拟试验而得出的，以使其α大体与准则1的α0=0.002 7相当。

图4-19　准则3的图示

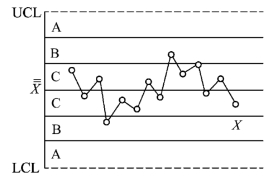
图4-20　准则4的图示

准则5：连续3个点中有2个点落在中心线同一侧的B区以外（图4-21）。

过程平均值的变化通常可由本准则判定，它对于变异的增加也较灵敏。这里需要说明：3个点中的2个点可以是任何2个点，第3个点可以在任何处，甚至可以根本不存在。出现准则5的现象是由于分布的参数μ发生了变化。

准则6：连续5个点中有4个点落在中心线同一侧的C区以外（图4-22）。

与准则5类似，第5个点可在任何处。本准则对于过程平均值的偏移也是较灵敏的。出现这种现象也是由于参数μ发生了变化。

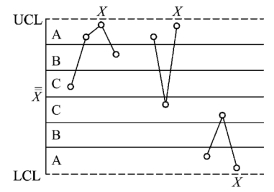
图4-21　准则5的图示

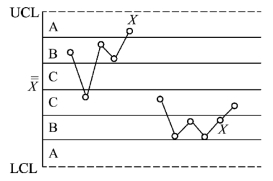
图4-22　准则6的图示

准则7：连续15个点在C区中心线上下（图4-23）。

出现这种现象是由于参数σ变小。对这种情况不要被它良好的“外貌”所迷惑，而应注意它的非随机性，造成这种现象的原因可能是数据虚假或数据分层不够等。

准则8：连续8个点在中心线两侧，但无一在C区中（图4-24）。

造成这种现象的主要原因是数据分层不够，本准则即为此而设计。

图4-23　准则7的图示

图4-24　准则8的图示

（十五）局部问题对策与系统改进

1.局部问题对策

由异因造成的质量变异可由控制图发现，通常由过程人员负责处理，称为局部问题的对策。这类问题约占过程问题的15%。虽然局部问题只占15%，但是一个系统早期出现的问题却往往是局部问题。

2.系统改进

由偶因造成的质量变异可通过分析过程能力来发现，但其改善往往需要耗费大量资金，须由高一级管理人员决定，称为系统改进。这类问题约占过程问题的85%。