1.疲劳寿命(S-N)曲线
疲劳强度设计一般以实验为基础,通过相应的力学实验获得某种构件的疲劳强度极限数据。疲劳试验需要在疲劳试验机上进行,为了降低实验成本和简化试验过程,通常采用结构简单、造价较低的标准试样。实验过程通常对试样施加不同幅值的零均值循环应力,并记录试样在循环应力条件达到破坏的循环次数或寿命N。通过对一组试样施加不同应力载荷的试验,可得到系列试验数据。经过数据处理后,以应力循环次数为横坐标,循环应力幅值为纵坐标,可以做出相应构件的循环应力-寿命曲线,通常称作S-N曲线。
图7-19反映了疲劳强度的S-N曲线的基本形式。S-N曲线多采用双对数坐标,曲线大致由三段折线组成。
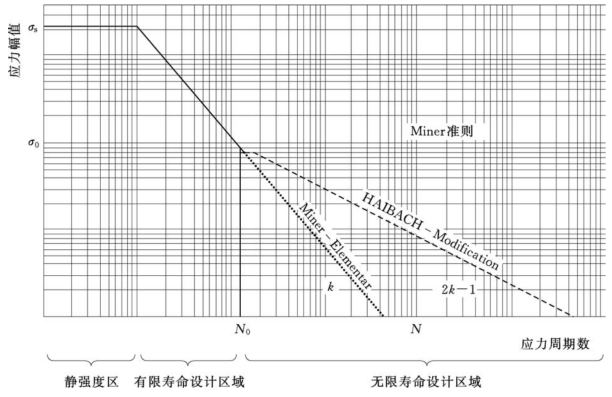
图7-19 典型的循环应力-寿命曲线(S-N曲线)
第一段为平行于横坐标的直线,一般对应材料的静载荷强度σs。
第二段为斜线,基本关系描述为
![]()
式中 m、C——与试件材料有关的常数;
Ni、σi——斜线上任意点坐标,亦即产生疲劳破坏的循环总次数Ni对应的循环应力σi,一般也称为条件疲劳强度。
第三段与第二段线交点的横坐标N0一般称为循环基数,对应的纵坐标σ0称为疲劳极限。
一般而论,当循环应力幅值低于σ0及试验循环次数超过N0时,若试件不发生损坏,则认为在σ0应力作用下,试件可以无限次循环而不出现疲劳失效。此种情况对应的第三段线呈水平线,也称为Miner准则。
但实际上,材料不可能承受无限次循环应力,对于风力发电机组等要求设计寿命较长的设备,特别是对于其中一些需要承受更高周次循环载荷的构件而言,仅采用Miner准则对应的低应力范围进行疲劳评估往往不够。
因此,为满足不同设计要求,有时需要采用其他的寿命估计方法,对Miner准则对应的第三段水平线进行修正。如图7-19所示,呈斜线的第三段疲劳特性分别对应了HAIBACH-Modificaiton和Miner-Elementar两种修正估计方法。一般认为后者更加合理。
图7-19中S-N曲线的第一、二段与循环基数N0所构成的区域,一般称为有限寿命设计区域。参照区域对应的疲劳极限条件进行的疲劳强度设计,称为有限疲劳设计。而超过N0区域对应的疲劳强度则被称为无限疲劳设计。
影响结构疲劳强度的因素很多,但主要涉及材料、零件状态和工作条件三个方面。
(1)材料方面:化学成分、金相组织、纤维方向、内部缺陷等。
(2)零件状态:应力集中系数、尺寸系数、表面加工状态、表面强化处理状态。
(3)工作条件:载荷特性、环境介质、使用温度等。
2.非零均值循环应力
如图7-20所示,循环应力具有周期变化的特点,其特征一般可描述为
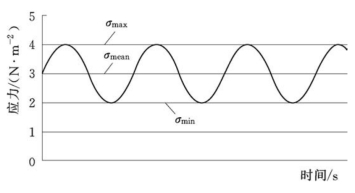
图7-20 循环应力及其特征

式中 σm——平均应力;
σmax——最大应力;
σmin——最小应力;
σa——应力幅值;
Δσ——应力范围。
以上这些参数被称为循环应力的特征参数。(https://www.xing528.com)
定义应力比RT,即
![]()
当循环应力为拉应力时取正值,为压应力时取负值。根据此应力比RT的取值,可区分循环应力的特征:RT=-1时,表示对称循环应力;RT=0时,为脉动循环应力;RT=1为静应力;当0<RT<1时,为波动循环应力;若应力比RT≠±1,所对应的各种循环应力统称为不对称循环应力。
在非零均值交变应力条件下,与对称应力的疲劳寿命曲线有所不同。若定义非零均值循环应力下的疲劳极限为σr、对称应力下的疲劳极限σ-1,两者存在如下关系:
(1)格伯关系。
![]()
(2)古德曼关系。

(3)索德贝尔格关系

式中 σb、σs——材料的强度极限和屈服极限。
可以利用式(7-24)~式(7-26)三种应力关系,对非零均值交变应力进行修正。但应注意,格伯关系比较复杂,通常适用于韧性材料,而索德贝尔格关系偏于保守。因此,在疲劳强度设计中较常用古德曼关系。
根据古德曼关系式,可将非零均值循环应力转换为等价的零均值循环应力,即

这样,即可以采用对称循环应力疲劳试验的数据,对非零均值循环应力作用下的构建疲劳寿命进行估计。
3.累积损坏与Miner准则
在承受小于寿命许用载荷条件下,部件也可能在连续运行一段时间后发生损坏。对于变幅值循环应力的情况,如图7-21所示,Palmgren和Miner分别提出了结构疲劳损伤的累积式线性的简单假设。

图7-21 变幅值循环应力
根据Miner对累积损坏的定义,累积损坏D为各幅值循环应力引起损坏的总和。若结构经受m个常幅循环应力σi(i=1、2、…、m),各应力下的寿命分别为Ni,发生ni次应力循环,则ni次循环造成的“相对损伤”为ni/Ni。当所有“相对损伤”的累积疲劳损伤总和等于1时,疲劳破坏发生。亦即

式中 ni——在各应力σi对应的循环次数;
Ni——单一应力σi作用下疲劳破坏的总循环次数;
D——应力幅值变化的情况下的累积总损伤。
这就是著名的线性损伤累积假设,已被广泛应用于变载荷条件的寿命分析中。
实际上,疲劳裂纹的形成和发展过程不一定是线性的,线性疲劳损伤累积理论也只是一种近似表达。但线性损伤累积的假设方法简单,基本能够满足工程应用要求。当然,针对一些特殊的设计需要,也可采用其他的寿命估计方法,如线性疲劳累积损伤理论等。
4.随机循环载荷
如图7-22所示,非周期性且与时间不具有确定函数关系的载荷称为随机载荷。随机载荷产生的疲劳现象通常称为随机载荷。随机载荷产生的疲劳现象通常称为随机疲劳。

图7-22 随机循环载荷
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




