垂直剪切风和横向风对XXX的影响

风不对称地吹扫过风轮时，会产生不稳定的、循环变化的载荷。受地表粗糙度的影响，风速随高度增加而增加，不可避免地造成了风的不均匀性。为此，风轮每旋转一圈，叶片在上部的旋转部位比离地面近的部位承受的风载荷更高。与此相似，由于横风风向的快速变化，也引起了风轮的循环变化载荷。

垂直剪切风和横风导致在叶片上循环地增加和降低气动载荷。与稳定而均匀的风产生的稳定载荷相比，产生了极大的差异，如图7-5所示。图7-5也反映了由于剪切风风轮廓和沿风向变化的不对称气流轮廓引起的叶片根部的弯曲应力。

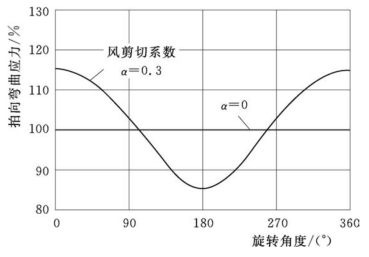
图7-5　由于剪切风引起的叶片根部的弯曲应力

在风轮旋转中，叶片气动载荷的变化也代表了风轮整体载荷的变化。对于非铰链连接的两叶片风轮，变桨距和偏航中的交变应力，造成偏航传动部件的疲劳载荷。基于此原因，大型两叶片风力机通常设计有铰链式轮毂，可在一定程度上补偿这些变化的载荷。

阵风导致风速在短时间内增加和风向的显著改变。但由于风力机的惯性和对风调向的滞后，风速增加后，风轮来不及作出反应快速增加转速，短时间内叶片表面气流相对速度很高；由于风轮轴不可能立即和已改变的风向一致，所以会发生30°～40°的对风偏差，甚至更多，结果使叶片承受的弯曲力矩增大。攻角α变化比气流相对速度w增大会引起更大的应力。

当产生横风，风轮对风不准时，设γ为风轮轴线与实际风向之间的夹角，如图7-6所示。距转轴γ处的叶片叶素气流的切向速度u=ωr，气流相对速度为

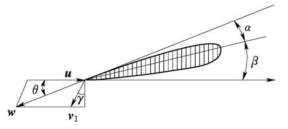
图7-6　对风不准时叶片气流速度三角形

其相对速度与切向速度间的夹角（入流角）为

(www.xing528.com)

可以看出，由于γ的存在，使叶片气流相对速度增加；而入流角减小，会使攻角减小。该叶素上垂直翼弦的空气动力为

式中 Cn——李连塞尔（Lilienthal）空气动力系数，取决于翼型和攻角α（α=θ-β）。

所以，对于已确定叶素翼型和安装角β的叶片，影响fn的因素有u（ω）、v1和偏航角γ。给定风力机角速度ω和风速v1时，取若干个偏航时出现的γ值进行计算，就可以求出任意距转轴r处的叶素上参量Cnw2可能达到的最大值，从而找出最大值fnM。

一般大型风力机叶片沿其长度的扭角都比较小，所以在确定叶片的弯曲应力时可以忽略沿其叶片的扭角。在此前提下，作用在叶尖值距离转轴z处叶片段的空气动力，对截面z所产生的最大弯曲力矩为

在距叶片根部z处叶片横截面的弯曲应力值为

式中 Jx——对于截面长度方向x-x中性轴的惯性矩，中性轴如图7-7所示；

c——从轴线到叶素翼型凸面一边的距离，m。

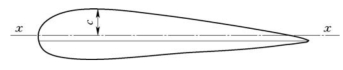
图7-7　叶片横截面长度方向中性轴