Betz定律指出了风轮机械输出功率的大小。叶素理论则指出风轮结构与其性能的关系。风轮功率P可以通过下式计算
式中 A——风轮扫风面积，m2；
v——风速度，m／s；
CP——风轮风能利用系数；
ρ——空气密度，kg／m3；
P——风轮功率，W。
对应某一叶尖速比，通过叶素理论可计算风能利用系数CP。重复对不同叶尖速比进行计算，则得出风轮风能利用系数与叶尖速比的关系曲线，该曲线也称为风轮功率特性曲线，表达了同一转速下不同风速的风能利用系数，或者同一风速下不同转速的风能利用系数。如果风轮采用变桨距控制功率输出，那么必须对每一桨距角的风能利用系数曲线进行计算。相应由不同桨距角的定桨距风轮性能曲线构成了变桨距风轮控制的性能曲线族，如图6-8所示。
图6-8 某风轮的性能曲线族
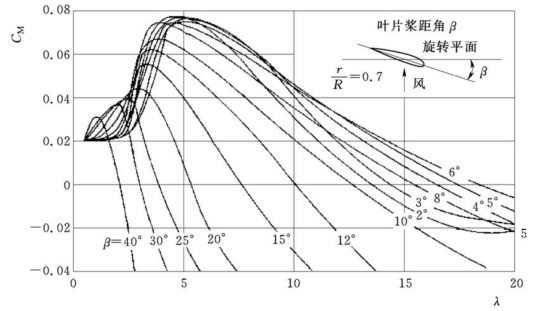
图6-9 某风轮的力矩曲线族
除了风轮输出功率外，风轮的动力矩也是反映风轮性能的重要参数之一，图6-9所示为不同桨距角对应的动力矩性能曲线。与功率类似，风轮动力矩可以通过力矩系数计算得到
(www.xing528.com)
式中 CM——风轮的力矩系数；
R——风轮半径，m。
由功率除旋转速度可计算得到力矩，故也可得出如下关系式
功率曲线和力矩曲线是风轮的性能特征曲线。风轮风能利用系数曲线形状的不同代表风轮结构的不同，影响CP的主要参数有风轮结构、风轮叶片数、叶片弦长分布、叶片气动性能、叶片扭角等。
图6-10所示为几种典型结构风轮的风能利用系数。从图6-10可看出，现代高速风轮较传统风轮具有明显的性能优势。如美国风车和荷兰风车的最大风能利用系数只有0.3，而利用气动阻力旋转的S型风轮则更低为0.15，现代三叶片水平轴风轮最大风能利用系数达0.5。
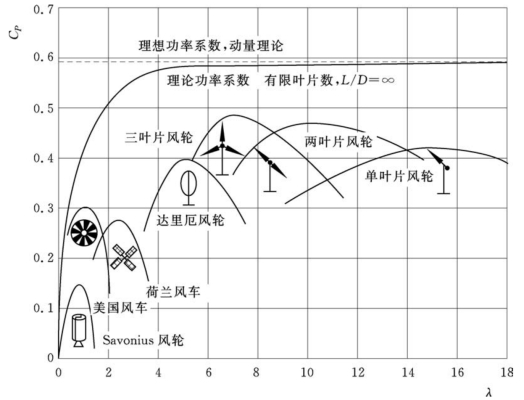
图6-10 不同风轮的风能利用系数
从图6-10还可看出，单叶片升力型风轮的最佳转速较两叶片的更高，最佳叶尖速比在15左右，但风能利用系数低于两叶片的；类似，两叶片升力型风轮的最佳转速较三叶片的更高，其最佳叶尖速比在10左右，风能利用系数则较低；三叶片风轮的最佳叶尖速比为7左右。
图6-11所示为五种典型风轮结构的力矩系数。从图6-11可看出，叶片密实度越小的风轮，最佳叶尖速比对应的最佳转速越快，风轮力矩越小；相反，叶片密实度较大的多叶片风轮，其最佳转速较低，力矩越大。两叶片风轮的起动力矩较小，因而很难起动，将风轮桨距角调到理想位置情况除外。
因此，从风轮的用途可大致确定风轮叶片数的范围。若用于乡村和偏远山区的提水或制热，可用叶尖速比较小的低速风轮，才能满足力矩要求。同样，对于当地年均风速不高的风资源，采用起动较好、叶尖速较低的风轮较为合适。
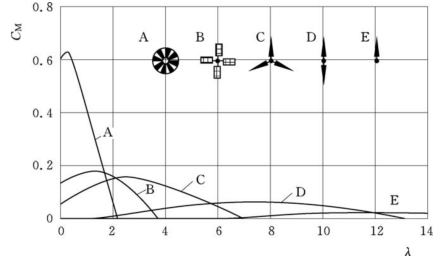
图6-11 不同结构风轮的动力矩
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
