贝兹理论及其对风能利用的限制

Betz理论定义的风轮为理想风轮，未涉及叶片的形状参数和气动参数。Betz理论主要考虑风力机轴向的动量变化，用来描述作用在风轮上的力与来流速度之间的关系，估算风力机的理想作功效率和流速。在风轮尾流不旋转时经典动量理论定义了一个通过风轮平面的理想流管，并假设：

（1）气流是不可压缩的均匀定常流。

（2）风轮简化成一个轮盘。

（3）轮盘上没有摩擦力。

（4）风轮流动模型简化成一个单元流管，如图5-12所示。

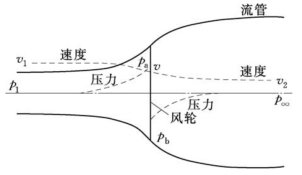
图5-12　风轮流动的单元流管模型

（5）风轮前后远方的气流静压相等。

（6）轴向力沿轮盘均匀分布。

将一维动量方程用于图5-12所示的控制体，考虑风力机轴向的动量变化，可得到作用在风轮上的轴向力推力T为

式中 v1——风轮前来流速度；

v2——风轮后尾流速度；

——单位时间流经风轮的空气质量流量。

可表示为

式中 ρ——空气密度；

A——风轮扫风面积；

v——流过风轮的速度。

将式（5-24）代入式（5-23）可以得出

根据动量理论，作用在风轮上的轴向力T表示为

式中 pa——风轮前的静压；

pb——风轮后的静压。

由伯努利方程可得

根据风轮前后远方的气流静压p1=p2相等的假设得出

(www.xing528.com)

由以上两式可以得出

上式表示流经风轮的速度是风轮前来流速度和风轮后尾流速度的平均值。

定义轴向诱导因子a=，v为风轮处轴向诱导速度，则

由式（5-32）可知，在风轮尾流处的轴向诱导速度是在风轮处的轴向诱导速度的两倍。轴向诱导因子a又可以表示为

式（5-33）表示如果风轮吸收风的全部能量，即v2=0，则a有一个最大值，a=。

但实际情况下，风轮只能吸收风的一部分能量，因此，a＜。

由式（5-30）和式（5-32）可得

引入风轮轴向力系数

则

根据能量方程，风轮吸收的能量（风轮轴功率P）等于风轮前后气流动能之差

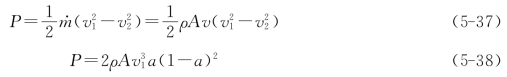
当=0时，则P出现极值，求解后a=1和a=。因为a＜，所以a=。此时，Pmax=

定义风轮风能利用系数

因此，当a=时，风轮风能利用系数最大，CPmax≈0.593。

由上述可分析，最大风能利用系数对应的风轮扫风面的空气流速度为

最大风能利用系数对应的风轮后空气流速度为

图5-13所示为风轮前后的流线、流速和压力的变化曲线图。从图5-13可以看出，在质量不变的条件下，由于风轮前后及风轮中的流速变化，使得流经风轮的空气流流管截面积发生变化。从流速曲线可以看出，在流经风轮时空气速度降为最低值，在风轮后速度逐渐增大为风轮前的流速。风轮从压力曲线可以看出，在靠近风轮处，静压力先骤然上升，然后骤然下降到最低点，且在风轮后逐渐恢复到最初的风轮前的压力值。

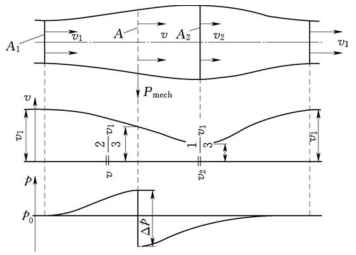
图5-13　风轮前后的流场参数变化曲线

通过上述分析可知，Betz理论实际上提出了风轮的最大转化率，即使是在无能量损失和理想空气流的条件下，风轮的风能利用系数也仅有0.593，也就是说，最大仅有59.3%的风能能够被风轮转化为机械能；其次，当理想风能利用系数等于0.593时，风轮后的空气流速为风轮前空气流速的。