深入了解威布尔分布

3.2.1.1 威布尔函数

威布尔分布是皮尔逊（Pierson）分布第三类的一个特例。在威布尔分布中，风速的变化用两个函数来表示：①概率密度函数；②累计分布函数。概率密度函数f（v）表明时间概率，风速用v表示，则

式中 k——威布尔形状因子；

c——比例因子，又称尺度参数。

速度v的累计分布函数F（v）提供了风速等于或低于v的时间（或概率）。因此，累计分布函数F（v）是概率密度函数的积分，故

根据威布尔分布，平均风速为

消去f（v），得到

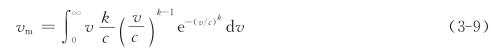
可化简为

设

将式（3-10）中的dv消去，得

这是标准伽马函数形式

因此，根据式（3-12），平均速度可表示为

根据威布尔分布，风速的标准偏差为

这里

消去f（v），据式（3-11）得到

表示为伽马积分的形式为

将方程（3-15）中的、vm替换掉，得到

图3-5和图3-6所示为根据威布尔分布得出的风况的概率密度和累计分布函数。场址中k和c的值分别为2.8和6.9。概率密度曲线的峰值表明风况中最常见的风速是6m／s。

图3-5　威布尔分布函数

图3-6　威布尔累积分布函数

累计分布函数可用来计算风在某一特定速度区间里的时间。风速在v1和v2之间的概率是由对应v2和v1的累计概率的不同来计算的，具体为

即

风速在超过vx时的概率可表示为

例：切入风速为4m／s、切出风速为25m／s的风力机安装在威布尔形状因子为2.4，比例因子c为9.8的风场内。一天内有多少小时风力机在发电？并计算出在该场址风速超过35m／s的概率。

一天内风力机发电时长为

0.89×24=21.36（h）

P（v＞v35）=e-（35／9.8）2.4=0.000000001

因此，风速超过35m／s的可能性是很小的。

根据威布尔分布，决定风能统一性的主要因素是威布尔形状因子k。图3-7和图3-8说明了形状因子k对概率密度函数和累积分布函数的影响。这里的比例因子c为9.8。风能的统一性随k的增加而增加。例如，当k=1.5，风速在95%的时间里分布于0～20m／s；如果k=4，速度在95%的时间里是更均匀地分布在0～13m／s的更小的范围里。前者最常见的风速是5m／s，预计占总时间的7.6%，而后者则将在15.5%的总时间内达到最常见风速9m／s。

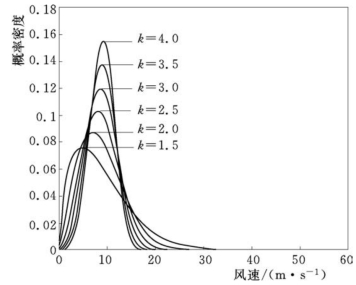
图3-7　不同比例形状对应的概率密度函数

图3-8　不同形状因子对应的累积分布函数(www.xing528.com)

3.2.1.2 威布尔参数计算方法

用威布尔分布来分析风况，必须估算出威布尔因子k和c。常用的确定k和c的方法有图解法、标准差法、矩量法、极大似然法、能量格局因子法。以下对每种方法分别进行说明。

1.图解法

在图解法中，将累积分布函数通过查对数表化为线性形式。风速累计分布可表示为

对式（3-23）两次取对数得

将X轴置为lnvi，Y轴置为ln｛-ln［1-F（v）］｝，绘制式（3-24）所示关系，得到一条较接近直线的曲线。根据式（3-24）得出，k是这条线的斜率，-klnc表示截距。如果用任意标准的电子表格或统计软件包来创立一个回归方程得到规划线，则可得出k和c的值。

例：某一场址风速的概率分布见表3-3。计算威布尔形状因子和比例因子。

表3-3　风速的概率分布

首先，根据给定的概率得出累计分布的数据。每一步都应当用上限值，如表格最后一栏所示。将X轴置为lnv，Y轴置为ln｛-ln［1-F（v）］｝，如图3-9所示，点比较分散。将这些点连成一条线，推导出最合适的方程。

图3-9　图形法来估计威布尔因子k和c

最终的方程为

数据和已确定的线之间的系数R2为0.98。结合式（3-24）和式（3-25），指定位置的k为2.24。同样，klnc=7.32。从这刻得出c为26.31km／h，即7.31m／s。

2.标准差法

威布尔形状因子k和c也可以通过风力数据的平均偏差和标准偏差计算出。考虑从式（3-14）和式（3-19）得出的平均偏差和标准偏差的表达式，可以得出

一旦σv值和vm值根据给定的数据计算得出后，通过上面的表达式k值就可以计算出。k值确定后，c的计算为

较为简单的方法是用下式来计算k的近似值

类似地，c可近似为

更确切地，c的计算为

例：用标准偏差的方法计算表3-3中的威布尔因子k和c。根据式（3-4）和式（3-5），平均偏差和标准偏差分别为28.08km／h（7.80m／s）和10.88km／h（3.02m／s）。

因此有

将vm和k代入式（3-30），得

此时可看出，用图解法和标准偏差法计算出的k和c值是不同的。图3-10所示为用这两种方法产生的累计分布与实地测量（点线表示）相比较。图解法得出的结果更接近实地测量值。标准偏差法在可接受的准确度范围内能预知风速分布。

图3-10　利用不同的方法来计算累积函数分布

3.矩量法

另一种计算k和c值的方法是一阶和二阶矩量法。威布尔分布n阶矩量Mn表示为

如果M1和M2是一阶和二阶矩量，利用式（3-31）可求解c，即

类似的

这种方法的M1和M2根据给定的数据计算得出，k和c通过解式（3-32）和式（3-33）求得。

4.极大似然法

用极大似然法，形状因子k和比例因子c的计算为

5.能量格局因子法

能量格局因子（EPF）是总功率和对应于平均风速三次方的功率的比值。因此，有

一旦风况的能量格局因子根据风力数据得出，k的近似解即为