平均风能密度的计算方法与分析

风能密度是评价风场优越性的一个重要参数。风能密度ED是流动空气在单位时间内垂直流过单位截面积的风能，其计算式如下

风能密度的单位为N·m／（s·m2），即W／m2。

在T时间段内，将式（2-32）对时间积分后平均，便得到T时间段内平均风能密度，即

一般情况下，风能统计所在地空气密度ρ的变化可以忽略不计，故式（2-33）可简化为

式（2-34）是理想状态下的计算公式，实践中风能密度的计算比较复杂。可直接利用观测资料计算平均风能密度。根据平均风能密度计算公式（2-32），先计算每个小时的风能密度，然后再求和，并按全年小时数平均，就可得到年平均风能密度。另外，也可以根据观测记录，像处理风频分布一样，把全部风速值分成许多段，每段为1m／s，把每段风速平均值的三次方乘以空气密度，再乘以该风速段全年发生的频率（该风速每年发生的小时数，小时／年），可得到如图2-30所示的风能分布曲线。并且可按下式计算该地的平均风能密度

从式（2-35）可以看出，平均风能密度也就是风能密度概率分布的数学期望。

也可以利用风速的概率分布计算风能密度。在已知风频概率分布函数的条件下，可以方便地计算平均风能密度。下面以威布尔（Weibull）分布为例进行说明。

根据风能密度的定义，风能密度ED只和空气密度ρ和风速v的三次方有关。空气密度ρ和风速v都可分别看作是具有一定概率分布规律的随机变量，ED作为两个随机变量的函数，也是一个随机变量。因此其数学期望E（ED）为

(www.xing528.com)

图2-30　风能分布

通常情况下，空气密度ρ和风速v无关，这时式（2-36）变为

对于指定地点，若取为其年平均密度，且为常数，在计算该地的年风能密度时，具有较高的计算精度。这样ED的概率分布特征实际上就只决定于风速v的概率分布特征了。决定平均风能密度的问题就简化为计算风速三次方数学期望的问题。

风速v服从威布尔分布的概率分布函数为

因此，风速立方的数学期望为

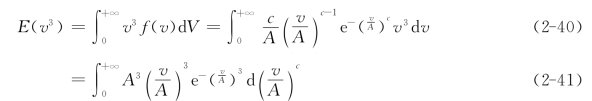
设y=（v／A）c，则有

可见，风速立方的概率分布依然是一个威布尔分布函数，不同的是其形状参数变为c／3，尺度参数为A3。