风廓线及其在风电场设计中的重要性

风速表示风移动的速度，即单位时间内风移动的距离，是描述风能特性的一个重要参数。

风速受地面粗糙度的影响颇大。植被、建筑物或其他地面设施增加了空气流动的阻力，导致地表附近的风速降低。随着离地面高度的增加，地表粗糙度对风速的影响减弱，风速随高度的增加而变大。随着地面粗糙度的增大，风速随距地高度增加而变化的现象愈加明显。定义这种风速随垂直高度增加而发生改变，形成的风速变化曲线为风廓线。

图2-9（a）所示为某场址典型的风廓线。从理论上讲，地面的风速应为零，在一定海拔下，速度随高度的增加而增大。气象观察表明，风速随高度增加的相对变化量因地而异。如图2-9（b）所示，在大城市环境下，从地面到高空45m／s的稳定风速需要550m的高度，而在农村则需要400m的高度，在海上仅需要300m的高度。下式描述了风速变化规律，即

式中 ——距离地面H0处的平均风速；

——高度H处的平均风速。

需要注意的是和为统计数据，式（2-3）只能拟合长期的气象观察结果，而对于单独的瞬时风速未必可行。式（2-3）中，幂指数n与表面粗糙度z0关系为

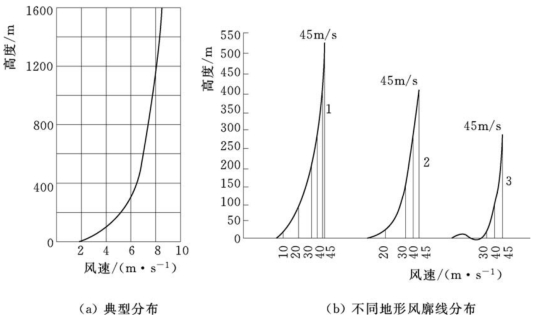
图2-9　风速随高度的变化曲线

1—大城市；2—城市和多树农村；3—平原和沿海

粗糙度z0是风电场设计中需要考虑的一个重要因素。假设风力机半径为30m，塔架高100m，叶尖最低处距地面70m，最高处距地面130m。若安装在如图2-9所示风廓线的地形，因不同高度的风速不相同，因此，作用在旋转叶片上的力和叶片获得的风功率也不相同。表2-1给出了不同地貌特征的粗糙度。

表2-1　不同地表面粗糙度的z0和n值的关系

气象观测站所获得的数据源于不同高度的传感器，根据世界气象组织的建议，以10m高度的风速作为当地风速。然而，风能计算所关注的通常是风力机轮毂高度近100m左右高度的风速。这要求在地形粗糙度的基础上，利用在任意高度收集的数据都可以得到其他高度的风速。(www.xing528.com)

由于边界层的影响，风速随高度以指数关系增大，可以利用式（2-3）进行计算，简单而精确。如果风速是在高度z、粗糙度z0下获得的，则高度zR处的风速由下式给出

式中 vzR、vz——zR和z处的速度。

如果10m处的风速为7m／s，粗糙度为0.1，高出地面40m处的速度就是9.1m／s 。但要注意的是40m高度处的功率是10m处的2.2倍。图2-10为以10m高度为基准的不同高度的风速比与粗糙度的影响曲线。

图2-10　相对于10m高度不同粗糙度的风速

一定条件下，需要参考某高度的气象数据，并将这些数据转变成其他具有相同的风速轮廓线，但粗糙度不同的风速数据。在这种情况下，可以假设超出某一特定高度后，风速受地表特性影响不明显。假设这个高度为距地面60m。因此，根据参考位置的速度可将60m处的速度表示为

此处的z0R是参考点处的粗糙度。考虑第二个位置

用式（2-6）除以式（2-7）得出

例：10m高度的气象站测出的风速为7m／s。确定出相同风速轮廓线的风电场高度为40m处的风速。天文台和风力机所处位置的粗糙度分别为0.03m和0.1m。则根据式（2-8）可得出