过滤效率理论计算方法

1.孤立纤维体的单项捕集效率

（1）惯性效率 对势流中的圆柱捕集体，Landah导出惯性效率半经验理论计算公式为

式中 S——Stokes数或称惯性踫撞系数，S=ρ_dd²_pv_o/18μd_c；

d_p——尘粒直径（m）；

v_o——流体特征速度（m/s）；

d_c——捕集体直径（m）。

可见，惯性效率随着Stokes数的增大而提高，也即对重质粗粉尘，加大过滤速度可以获得较高的惯性效率。

（2）拦截效率 对围绕圆柱体的黏性流，Langmuir导出拦截效率计算公式为

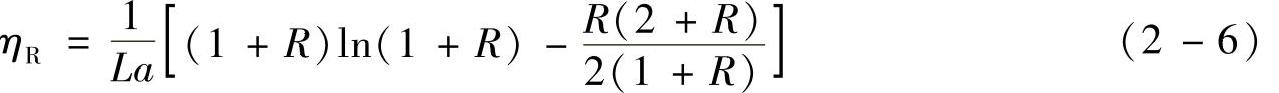
式中 La——拉氏系数，La=2.002-lnRec；

R——截留系数，R=d_p/d_c；

Rec——黏性流流经捕集体的雷诺数，Rec=ρ_gd_cv_o/μ。

当R＜0.07时，η_R≈R²/La。可见拦截效率主要与截留系数相关，随尘粒直径的加大和捕集体直径的减小而提高。

（3）扩散效率 对纤维层过滤器，Langmuir导出扩散效率计算公式为

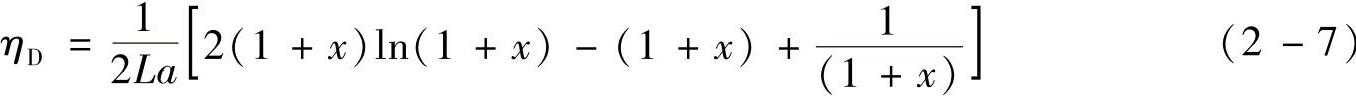
式中 x=1.308（La/Pe）1/3；

Pe——贝克来（Peclet）数，Pe=v_od_c/D；

D——扩散系数。

可见，扩散效应仅对细微尘粒起作用，并且缩小纤维直径、降低过滤速度、提高气体温度可以增强扩散效果。

（4）静电效率 过滤体的静电效应分为三种情况：一是捕集体荷电，尘粒中性，此时粉尘感应产生反相镜像电荷而相互吸引；二是尘粒荷电，捕集体中性，此时捕集体感应产生反相镜像电荷而相互吸引；三是粉尘、捕集体都荷电，此时视荷电性状，异性相吸，同性相斥。

在自然状态下，即不予施加静电场时，捕集体的静电效应是不稳定的。相对而言，第一种情况（即捕集体带电，尘粒中性）是最易发生的。这种情况的静电效率计算公式为

η_E=1.68N¹/3 （2-8）

式中 N——静电力无因次参数，；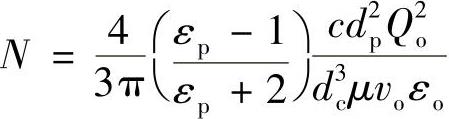

Q_o——单位长度捕集体电荷量（C）；

ε_p——尘粒介电常数（F/m）；

ε_o——捕集体介电常数（F/m）；(www.xing528.com)

c——Cunningham修正系数。

可见，静电效应的机理十分复杂，涉及的影响因素较多。关键是如何保持稳定的静电效应。近期开发的粉尘预荷电以及驻极体纤维滤料是利用并提高捕集体静电效应的有效措施。

2.邻近纤维的影响

纤维层由众多单一纤维体组成，平面纤维层中单一纤维体的流场不同于孤立纤维体的流场，流速较高，从而有利于提高捕集效率。可以对每一种捕集效率引入一个包含纤维填充率的函数项加以修正，即

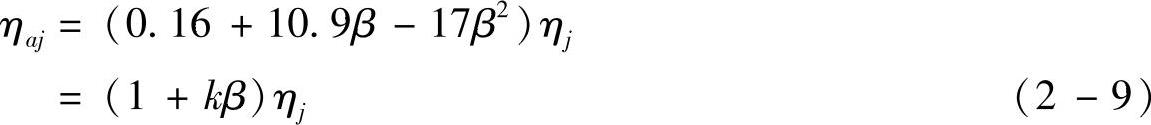
式中 β——纤维的填充率；

η_j——孤立纤维体各种机理捕集效率（j=I、R、D、E）；

k——试验系数，平均值约为4.5。

可见，纤维的填充率越大，纤维层的分项捕集效率越高。

3.纤维体总捕集效率

孤立纤维体的总捕集效率受制于各单项捕集效应的综合作用，可用下式计算：

η_a=1-（1-η_Ι）（1-η_R）（1-η_D）（1-η_E） （2-10）

对于大于1μm的尘粒，以惯性碰撞、拦截和重力效应为主，Davies导出近似计算式为

η_IR=0.16[R+（0.5+0.8R）S-0.1052RS²] （2-11）

对小于0.2μm的尘粒，以分子扩散和静电效应为主，Langmuir导出近似计算式为

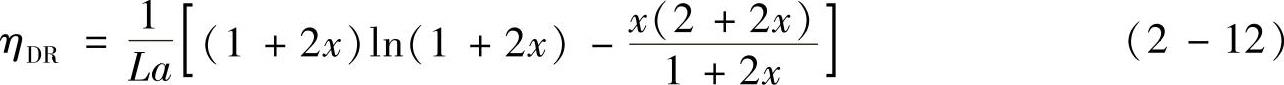
图2-7 为单项捕集效率和综合捕集效率与粒径的分布曲线。

4.纤维层的捕集效率

纤维层是一个三维过滤结构，比单纤维体具有更高的捕集效率，其总效率可用下式计算：

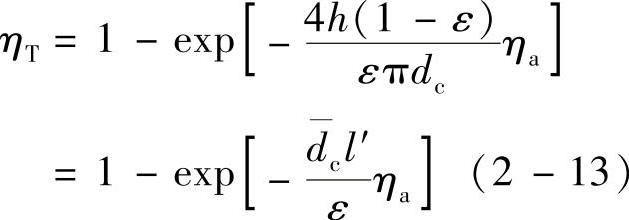
式中　h——纤维层厚度（mm）；

ε——纤维层空隙率（%）；

d_c——平均纤维径（μm）；

l′——“有效”纤维长度。

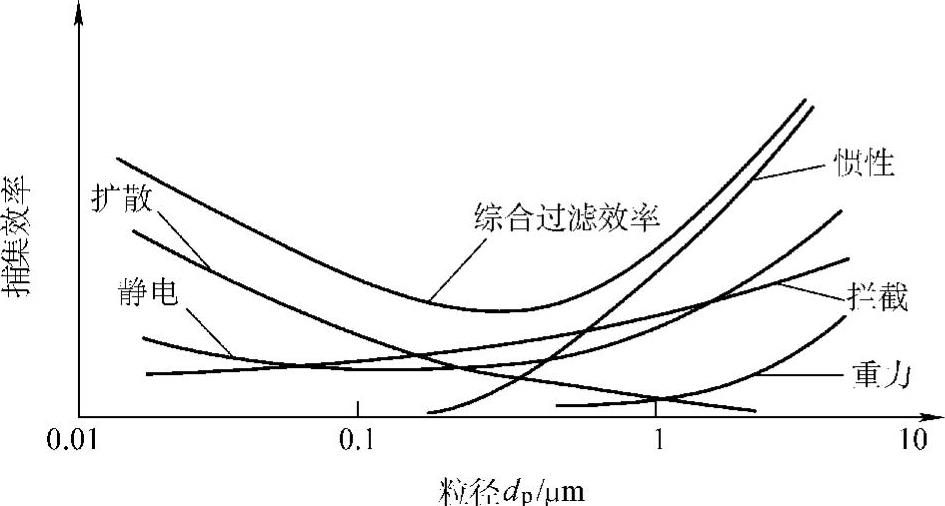
图2-7 捕集效率与粒径的分布曲线