含尘气体的流体力学特性分析

1.尘粒在气体中的运动

当尘粒受机械力作用以v₀初速度作水平运动时，由于气体的阻力，尘粒呈减速运动，可用下式表达尘粒的运动规律：

尘粒运动的末速度为

v=v₀e^-t/τ （1-9）

尘粒在时间t内运动的距离为

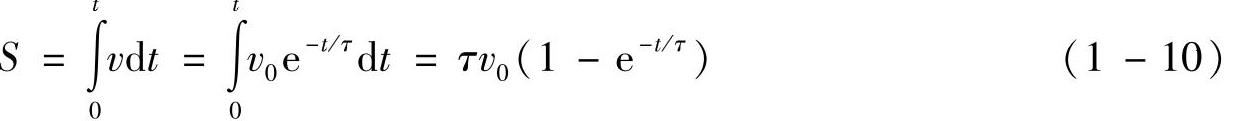
式中 τ——非稳态颗粒在连续流体系运动的弛豫时间（s），τ=d²_cρ_c/18μ；

d_c——尘粒的直径（m）；

ρ_c——尘粒的密度（kg/m³）；

μ——气体的动力粘度（Pa·s）。

2.尘粒在气体中的凝聚

在气固两相流动中，引起颗粒碰撞凝聚的作用力分为三类：

1）流体给予的作用力，如分子扩散、湍流扩散、流体曳力等；

2）颗粒间的相互作用力，如库仑力、毛细吸附力等；

3）外力，如静电力、磁力、声力、重力等，颗粒还可以被液滴或液膜黏附进行聚集从而被分离。

单个粒子通过凝聚趋于形成粒子聚集体，并最终因重量不断增加而沉降；聚集体成长得越大，沉降得越快。

3.尘粒在气体中的沉降

尘粒沉降速度为

式中 v_s——尘粒沉降速度（m/s）；

ρ_c——尘粒密度（kg/m³）；

ρ_g——气体密度（kg/m³）；

g——重力加速度（m/s²）；

d_c——尘粒直径（m）；

C_D——气体阻力系数，其值与尘粒与气流间相对运动Re有关。

通常在通风除尘工程中，Re≤1时，则C_D=24/Re，代入式（1-11），可得简化式：

4.尘粒在气体中的惯性碰撞

非稳态颗粒在连续流体系运动的弛豫时间为

粒径微细的颗粒乘以肯宁汉修正因子，对球形颗粒则为(www.xing528.com)

式中 m_c——粒子质量（kg）；

C——肯宁汉修正因子，见表1-7。

表1-7 肯宁汉修正因子（在20℃，101325Pa空气中）

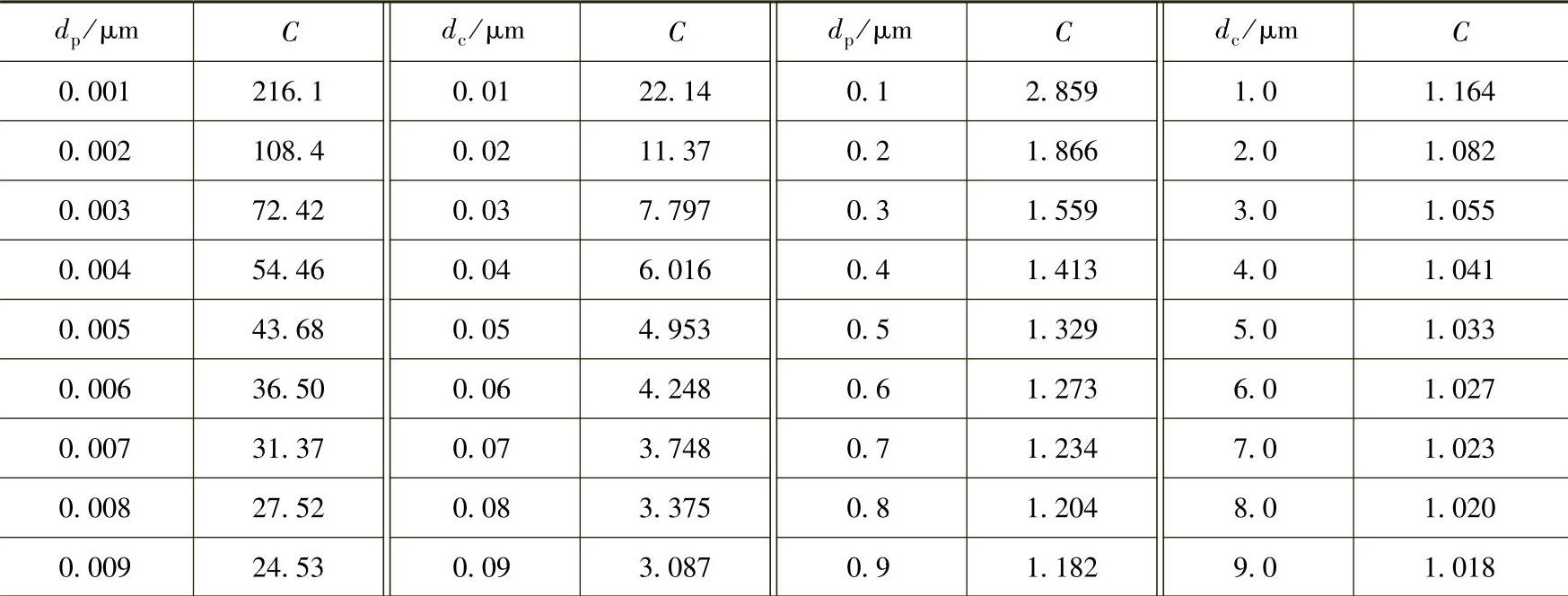
颗粒以一定的初速度v₀运动，去掉外力后，颗粒因阻力而减速直至停止的距离：

X_s=v₀τC （1-15）

式中 v₀——颗粒运动的初始速度（m/s）；

τ——颗粒的弛豫时间（s），见式（1-13）；

C——肯宁汉修正因子。

惯性碰撞效应可用惯性参数或用下式斯托克斯数（St）表征：

则球形捕集体的惯性碰撞效率，可用下式近似推算：

5.尘粒在气体中的离心分离

离心分离中，处于外涡旋的尘粒在径向受到离心惯性力和向心黏性力的共同作用：

1）惯性离心力

式中　v_t——尘粒的切线速度，可以近似认为等于该点气流的切线速度（m/s）；

r——旋转半径（m）。

2）向心黏性力：

P=3πμωd_c （1-19）

在内外涡旋交界面上，当F₁=P时的粒径为分割粒径，即

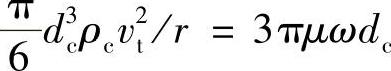
则分割粒径d_c50（m）

式中 μ——气体动力粘度（Pa·s）；

r₀——交界面的半径（m）；

ω₀——交界面上的气流径向速度（m/s）；

v_t0——交界面上的气流切向速度（m/s）。