无序号算术编码：自适应高效的编码方法

算术编码也是一种利用信源概率分布特性的，能够趋近熵极限的编码方法。其编码原理与哈夫曼编码不同，最大的区别在于算术编码跳出了分组编码的范畴，它在编码时不是按符号编码，即不是用一个特定的码字与输入符号之间建立一一对应的关系，而是从整个符号序列出发，采用递推形式进行连续编码，用一个单独的算术码字来表示整个信源符号序列。它将整个符号序列映射为实数轴上[0，1）区间内的一个小区间，其长度等于该序列的概率。从小区间内选择一个代表性的二进制小数，作为实际的编码输出，从而达到高效编码的目的。不论是否为二元信源，也不论数据的概率分布如何，其平均码长均能逼近信源的熵。

算术编码过程是在[0，1）区间上的分过程，下面举例说明算术编码的具体过程。

【例4-1】 假设信源符号为{A，B，C，D}，这些符号出现的概率分别为{0.1，0.4，0.2，0.3}，根据这些概率可把区间[0，1）分成4个子区间：[0，0.1），[0.1，0.5），[0.5，0.7），[0.7，1），其中[x，y）表示半开区间，即包含x不包含y。如表4-1所示。

表4-1 信源符号、概率和初始编码区间

如果符号序列的输入为：C A D A C D B。编码时首先输入的符号是C，找到它的编码区间是[0.5，0.7）。由于序列中第二个符号A的编码区间是[0，0.1），因此它的区间就取[0.5，0.7）的第一个1/10作为新区间[0.5，0.52）。以此类推，编码第3个符号D时取新区间为[0.514，0.52）；编码第4个符号A时，取新区间为[0.514，0.5146）；……。符号序列的编码输出可以是最后一个区间中的任意数，其整个编码过程如图4-3所示。

这个例子的编码全过程如表4-2所示。

解码是编码的逆过程。这个例子的解码全过程如表4-3所示。

在编码过程中的乘法运算可以通过移位实现，即通过加法和移位实现算术编码。在解码时，要除以符号区间概率，这也可以通过移位实现，即通过减法和移位实现算术解码，因此这种编码方法称为算术编码。

图4-3 算术编码过程

表4-2 编码过程

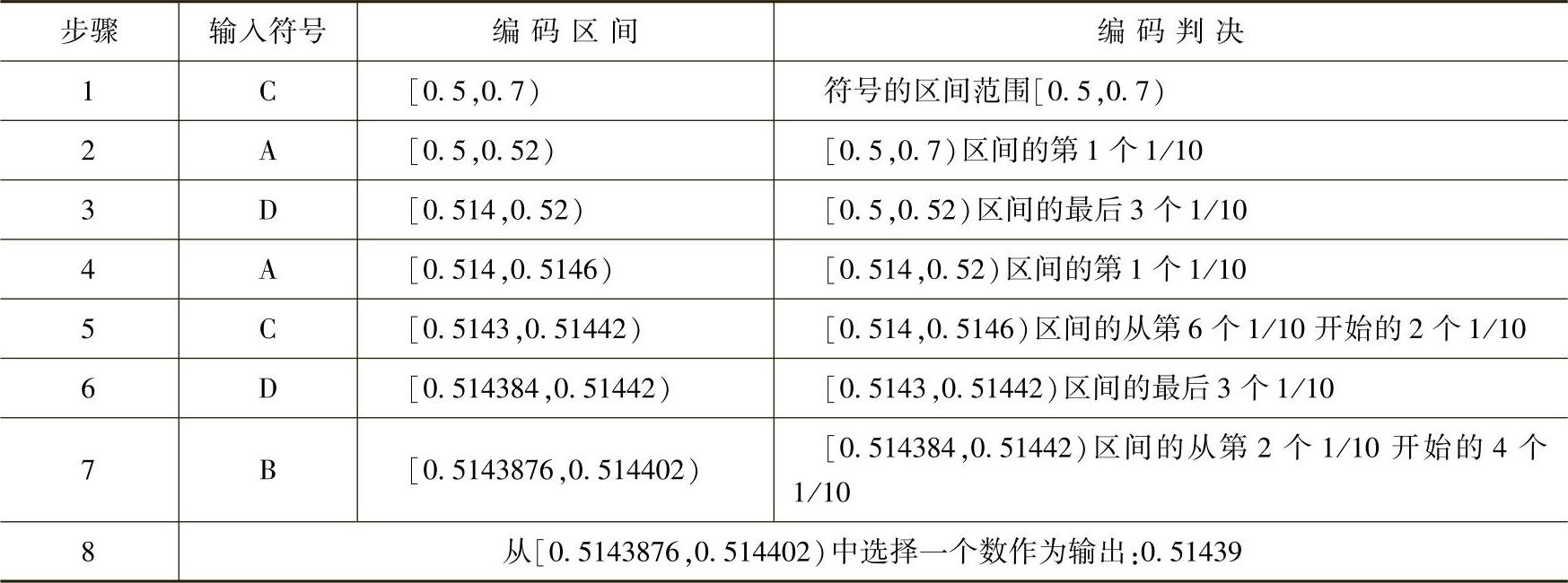
表4-3 解码过程

那么算术编码与符号的排列顺序是否有关呢？早在1948年，香农（Shannon）就提出将信源符号按其概率降序排列，用符号序列累积概率的二进制表示作为对信源的编码；1960年后，P.Elias发现无需排序，只要编、解码端使用相同的符号顺序即可，但仍需要无限精度的浮点运算；1976年，R.Pasco和J.Rissanen分别用定长的寄存器实现了有限精度的算术编码，但仍没有解决有限精度计算固有的进位问题。

从上面的例子中发现，随着输入符号越来越多，子区间分割越来越细，因此表示其左端点的数值的有效位数也越来越多。如果等整个符号序列输入完毕后再将最终得到的子区间左端点输出，将遇到以下两个问题：

1）当符号序列很长时，将不能实时编解码。

2）有效位太长的数难以表示。

为了解决这两个问题，通常采用两个有限精度的移位寄存器存放码字的最新部分，随着序列中符号的不断输入，不断地将其中的高位移到信道上，以实现实时编解码。

具体编码过程中，如果子区间左端点和右端点中的最高位相同，则相应的位将保持不变。按照这种原理，只要出现相同的最高位就将它移出，保证寄存器中的位数不发生溢出。另外，将1.0表示为0.1111111……，以便移位操作。

下面通过一个例子分析应用移位寄存器的算术编码及解码过程。

【例4-2】 设信源符号表是{a_l，a₂，a₃，a₄}，其符号出现的概率分别为{0.5，0.25，0.125，0.125}。如果输入序列为a₂a₃a₄，其算术编码的分过程如图4-4所示。(www.xing528.com)

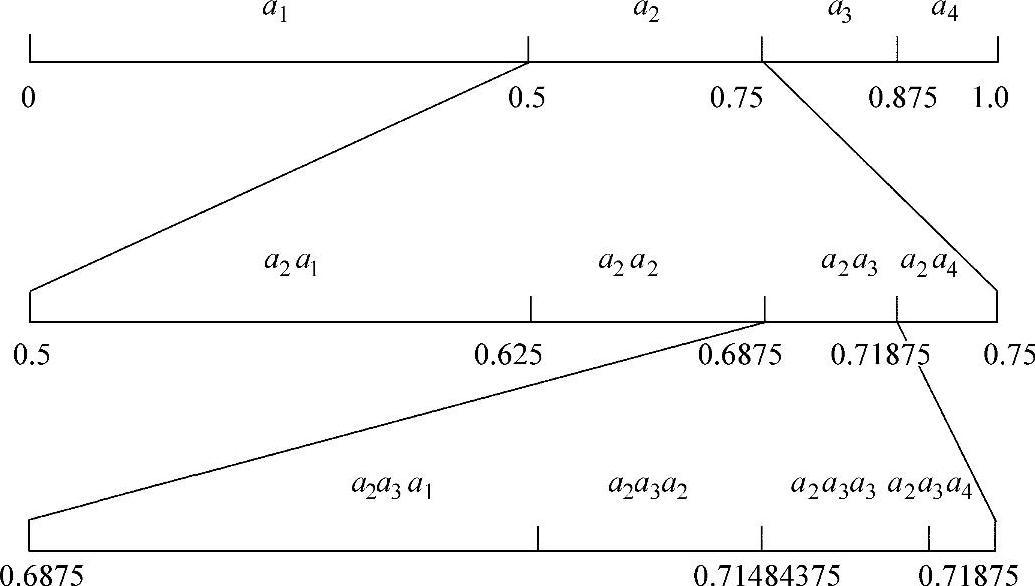
图4-4 算术编码的分过程

该符号序列的编码过程如表4-4所示，由表可知最终a₂a₃a₄的区间为[0.71484375，0.71875）。

表4-4 算术编码过程

应用8位移位寄存器的编码过程如表4-5所示，表中将十进制小数转化为二进制小数，如0.5表示为0.10000000。移位时要注意，右端点寄存器的右边移进来的是1，而左端点寄存器右边移进来的是0。求得的右端点0.11应表示为0.10111……。

表4-5 应用8位移位寄存器的编码过程

a₂a₃a₄序列的编码结果是10110111。

解码过程如下：

接收端收到的比特串是10110111，解码是将该比特串通过与限定区间逐次比较还原码序列的过程。

当收到第1个比特“1”时，将子区间限定在[0.10000000，0.11111111），表示区间[0.5，1.0），对照图4-4，由于有3个符号都可能在此范围内，即a₂、a₃或a₄。因此，仅有第一个比特还不足以解出第一个符号，需要参考后续的比特。

当收到第2个比特“0”时，将子区间限定在[0.10000000，0.10111111），表示区间[0.5，0.75），能够解出a₂。

当收到第3个比特“1”时，先将前面解出的a₂对应的码字“10”去掉，将子区间限定在[0.10000000，0.11111111），表示区间[0.5，1.0），限定在3个符号范围内，即a₂、a₃或a₄还不能确定，因此，需要参考后续的比特。

当收到第4个比特“1”时，将子区间限定在[0.11000000，0.11111111），表示区间[0.75，1.0），限定在两个符号范围内，即a₃和a₄还不能确定。

当收到第5个比特“0”时，将子区间限定在[0.11000000，0.11011111），表示区间[0.75，0.875），能够解出a₃。

同理，解出最后一个符号a₄，最终得到解码结果为a₂a₃a₄。

算术编码的最大优点在于它具有自适应性和高的编码效率。算术编码的模式选择直接影响编码效率，其模式有固定模式和自适应模式两种。固定模式是基于概率分布模型的，而在自适应模式中，其各符号的初始概率都相同，但随着符号顺序的出现而改变，在无法进行信源概率模型统计的情况下，非常适合使用自适应模式的算术编码。

在信源符号概率比较均匀的情况下，算术编码的编码效率高于哈夫曼编码。但在实现上，由于在编码过程中需设置两个寄存器，起始时一个为0，另一个为1，分别代表空集和整个样本空间的积累概率。随后每输入一个信源符号，就更新一次，同时获得相应的码区间，解码过程也要逐位进行。可见计算过程要比哈夫曼编码的计算过程复杂，因而硬件实现电路也要复杂些。

算术码也是变长码，编码过程中的移位和输出都不均匀，也需要有缓冲存储器。

在误差扩散方面，也比分组码更严重。在分组码中，由于误码而破坏分组，过一段时间后常能自动恢复；但在算术码中，往往会一直延续下去，因为它是从全序列出发来编码的。因而算术码流的传输也要求高质量的信道，或采用检错反馈重发的方式。

注意，在实际应用中有两个因素会影响编码性能而使编码结果达不到理论极限：一是为了分开各个符号序列需要加序列结束标志；二是算术操作的精度是有限的。