信号数字化的意义与方法

信号的数字化就是将模拟信号转换成数字信号，一般需要完成采样、量化和编码三个步骤。采样是指用每隔一定时间（或空间）间隔的信号样本值序列代替原来在时间（或空间）上连续的信号，也就是在时间（或空间）上将模拟信号离散化。量化是指用有限个幅度值近似表示原来连续变化的幅度值，把模拟信号的连续幅度变为有限数量、有一定间隔的离散值。编码则是按照一定的规律，把量化后的离散值用二进制数字表示，以便进行传输或记录。

1.采样

模拟信号不仅在幅度取值上是连续（连续的含义是在某一取值范围内可以取无穷多个数值）的，而且在时间（或空间）上也是连续的。要使模拟信号数字化，首先要在时间（或空间）上进行离散化处理，就是在时间（或空间）上用有限个采样点来代替连续无限的坐标位置，这一过程叫采样。所谓采样就是每隔一定的时间（或空间）间隔，抽取信号的一个瞬时幅度值（样本值）。采样后所得出的一系列在时间（或空间）上离散的样本值称为样值序列。采样的示意图如图3-1所示。

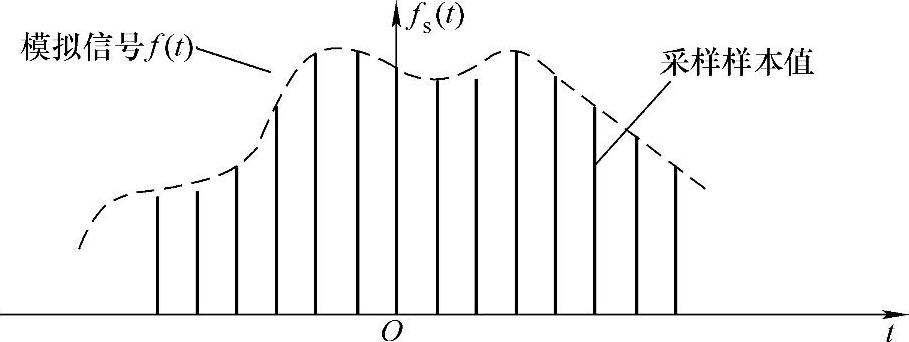
图3-1 采样示意图

根据奈奎斯特（Nyquist）采样定理，只要采样频率大于或等于模拟信号的最高频率的两倍，即f_s≥2f_max，就可以通过理想低通滤波器，从样值序列中无失真地恢复出原始模拟信号。也就是说，在满足奈奎斯特采样定理的条件下，在时间上离散的信号包含有采样前模拟信号的全部信息。

在数字图像压缩编码中，为进一步提高压缩比，一种不满足奈奎斯特采样定理的亚采样及其内插技术也是目前研究热点之一。

2.量化

采样把模拟信号变成了时间（或空间）上离散的样值序列，但每个样值的幅度仍然是一个连续的模拟量，因此还必须对其进行离散化处理，将其转换为有限个离散值，才能用有限个二进制数来表示其幅值。这种对采样值进行离散化的过程叫做量化。

量化既然是以有限个离散值来近似表示无穷多个连续量，就一定会产生误差，这就是所谓的量化误差，由此所产生的失真就是量化失真或量化噪声。

当量化器的每个量化间隔都相等，量化电平取各量化区间的中间值时，称这种量化为均匀量化或线性量化。可以证明，量化误差的均方值与量化间隔的平方成正比。量化间隔越小，量化误差就越小，但用来表示一定幅度的模拟信号时所需要的量化级数就越多，编码时所用的比特数就越多，这不利于数据的传输和存储。所以，量化时既要尽量减少量化级数，又要使量化失真看不出来。所谓量化比特数是指要区分所有量化级所需的二进制码位数。(www.xing528.com)

在进行二进制编码时，所需的二进制码位数n与量化级数M之间的关系为

M=2ⁿ或n=log₂M

对于双极性信号（如声音信号），其量化信噪比用信号功率与量化噪声功率之比表示，即

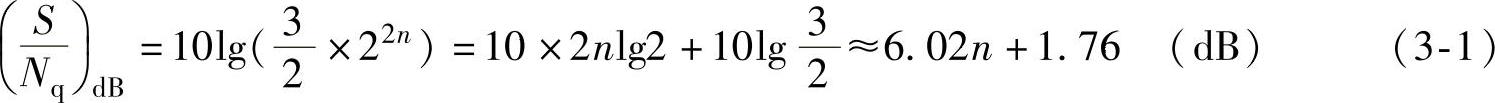
视频信号的量化信噪比一般用信号峰-峰值与量化噪声平均功率的方均根值之比表示，即

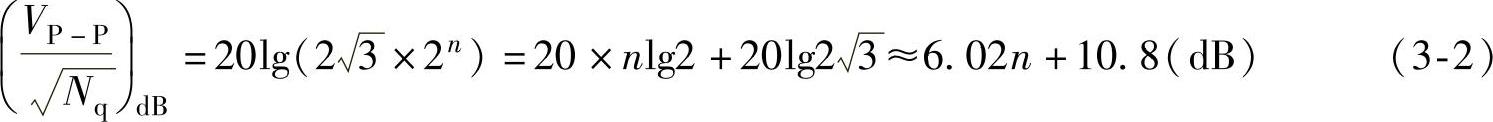
由量化信噪比表达式可以看出，量化比特数n每增加或减少1bit，就使量化信噪比提高或降低6dB。

3.编码

采样、量化后的信号还不是数字信号，还需要把它转换成数字编码脉冲，这一过程称为编码。最简单的编码方式是二进制编码。具体说来，就是用n比特二进制码来表示已经量化了的样值，每个二进制数对应一个量化电平，然后把它们排列，得到由二值脉冲组成的数字信息流。

数字信号的传输速率（通常也称为比特率或数码率）等于采样频率与量化比特数的乘积。显然，采样频率越高，量化比特数越多，传输速率就越高，所需要的传输带宽就越宽。