快速傅里叶变换（FFT）简介及应用

快速傅里叶变换是指利用计算机计算离散傅里叶变换（DFT）的高效、快速计算方法的统称，其本质仍然是DFT。它是1965年由J.W.库利和T.W.图基提出的，采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著，如图 2-3-12 所示。

图2-3-12　DFT与FFT执行时间比较示意图

FFT的出现解决了离散傅里叶变换的计算量极大、不实用的问题，从而使离散傅里叶变换得到了广泛应用。我们常用的信号处理软件MATLAB或者DSP软件包中，包含的算法都是FFT而非DFT。

通过上述信号时域分析和频域分析，可得到如下结论：

（1）傅立叶分析理论的核心思想和方法与数学中的牛顿—莱布尼兹微积分理论的思想有相似之处，即“化整为零，积零为整”，也就是将复杂问题分割成许多相对简单的问题来分别处理，再对处理后的简单问题合理整合，从而完成对复杂问题的处理和解决。迁移到分析信号，就是将信号分解为某种最简单的单一信号的组合。在时域分析中，将任意信号分解为一系列不同强度的冲激信号的移位加权和，而在频域分析中则是将任意信号分解为以正弦（虚指数）信号为基础的各谐波分量的加权和。例如，连续周期信号分解为，连续非周期信号分解为ejωt，离散周期信号分解为，离散非周期信号分解为ejkΩn。之所以用正弦信号来表示任意信号，主要包括两个重要原因：一是正弦信号比原信号更简单，且正弦函数很早就已经被充分研究；二是正弦信号具有频率保持性，即对于线性时不变系统，输入为正弦信号，输出仍是正弦信号，幅度和相位可能发生变化，但频率与原信号保持一致，也只有正弦信号才具这个性质。

（2）连续形式的傅里叶变换其实是傅里叶级数的推广，因为积分其实是一种极限形式的求和算子。理解这种推广过程的一种方式是将非周期性现象视为周期性现象的一个特例，即其周期为无限长。

（3）信号“域”的不同，是指信号的自变量不同，或描述信号的横坐标物理量不同，信号在不同“域”的描述使所需信号的特征更为突出，以便满足解决不同问题的需要。但是，无论采用哪种描述方法，同一信号含有的信息和能量是相同的，即信号在不同“域”间转换时不增加新的信息和能量。

（4）时域和频域具有严格的映射关系，一个域的“离散”对应另一个域的“周期”延拓，一个域的“连续”对应另一个域的“非周期”，信号在一个域越窄，在另一个域越宽，且易证明：

表2.3-1详细列出了六种傅里叶变换中信号时域特性与频域特性的映射关系。

表2-3-1　信号时域特性与频域特性的映射关系

常用信号的傅里叶变换列于表2-3-2中，可供查阅。

表2-3-2　常用信号的傅里叶变换表

续表

在运用计算机对连续信号进行傅里叶变换时，主要关注频谱分布范围和频谱分辨率这两个指标。

频谱分布范围指的是能够观察到的频率范围，若信号的最高频率为fH，抽样频率为f（s应保证fs≥2fH），则频谱分布范围为。

频谱分辨率Δf表示能够分辨的两个频率分量的最小间隔，其值为（NTs称为记录时间）。(www.xing528.com)

可见，更宽的频谱范围取决于对原始信号的抽样频率fs，若想提高频谱分辨率，当采样点数 N 不变时，就必须降低抽样频率，但降低抽样频率会引起频谱范围变窄和频谱混叠，当抽样频率不变，就必须增加采样点数 N，即增加对信号的记录（采样）时间，这就对设备的长存储能力提出了更高要求。下面结合实例谈一下相关参数的取值。

【例2-3-5】假设模拟信号的最高频率fH为 2.5 kHz，要求频谱分辨率F≤10 Hz，

求：（1）最小记录时间、最大的采样间隔、最少的采样点数。

（2）若保持最高频率fH不变，要求频谱分辨率提高1倍，最少的采样点数和最小记录时间。

解：根据公式可知，最小记录时间为

按照抽样定理，要求fs≥2fH，则最大的抽样间隔为

最少的抽样点数为

为了使用DFT的快速算法FFT，希望N为 2 的整数幂，因此选用N=512。

为了使频谱分辨率提高1倍，即Δf＝5 Hz，则

最少的抽样点数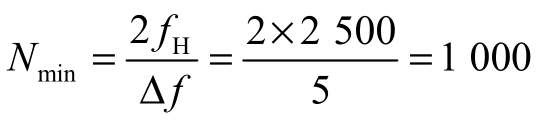

最小记录时间为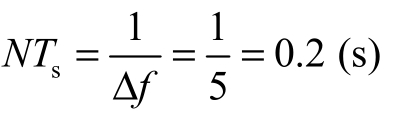

采用快速算法FFT计算时，N应取 1 024 点。

【例2-3-6】设计要求的系统带宽为 1 MHz，频率分辨率不高于 10 kHz，求最小记录时间、最大的采样间隔、最少的采样点数。

解：根据公式可知，N应选256，此时