傅里叶变换的性质详解

傅里叶变换的性质包括线性、对称性、尺度变换、时移特性、频移特性、时域卷积定理、频域卷积定理、时域微分和积分、频域微分和积分等性质。这里主要介绍时移特性和频移特性。

1.时移特性

若信号f(t)的频谱为F(jω)，即f(t)↔F(jω)，则信号f(t−t0)的频谱为，即。

时移特性表明：信号f(t)在时域中沿时间轴右移（延时）t0个单位等效于在频域中频谱乘以因子；若信号f(t)沿时间轴左移（提前）t0个单位，则其频谱应乘以因子。

2.频移特性

若信号f(t)的频谱为F(jω)，即f(t)↔F(jω)，则信号的频谱为F[j(ω−ω0)]，即。

频移特性表明：信号f(t)乘以因子（或），则其频谱沿频率轴右移（或左移）ω0个单位。

上述频谱沿频率轴右移或左移称为频谱搬移技术。在通信系统中可用于实现调制、变频及同步解调等过程。频谱搬移的基本原理是将f(t)乘以载频信号cos(ω0t)或者sin(ω0t)。即

同理

式（2-3-8）表明：一个时间信号f(t)与正弦信号sinω0t相乘，它的频谱F(jω)将搬移到ω=ω0和ω=−ω0处，其幅度为原来的一半。

【例2-3-3】如图 2-3-7（a）所示，单个矩形脉冲信号的表达式可表示为

解：由式（2-3-6）可知，f(t)的频谱F(jω)为

式（2-3-9）中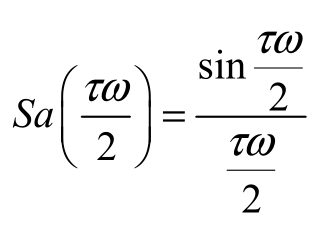，称为抽样函数。故f(t)的频谱F(jω)如图2-3-6（b）所示。

图2-3-7　单个矩形脉冲信号的波形和频谱(www.xing528.com)

图 2-3-6 和 2-3-7（b）所示的频谱能量主要集中在范围，为了传输这样的矩形脉冲，在实际应用中，把第一个过零点的位置作为带宽就够了，即认为矩形脉冲的带宽等于其脉冲持续时间τ的倒数，即，此带宽称为过零点带宽。需要说明的是，在通信系统中，除了用过零点带宽来表示信号的频率分布，还可以用绝对带宽3 dB 带宽（也叫半功率带宽）来表示。其中绝对带宽表示为上限频率fH与下限频率fL之差，即

B=fH−fL

关于 3 dB 带宽的叙述详见第 3 章。

【例2-3-4】试求单位冲激信号的频谱（密度）。

解：由于单位冲激信号δ(t)为非周期信号，根据非周期信号傅里叶变换的公式，可得单位冲激信号δ(t)的傅里叶变换为

式（2-3-10）表明，单位冲激函数的频谱密度等于 1，即它的各频率分量连续且均匀分布在整个频率轴上，常称为“均匀谱”或“白色频谱”，如图 2-3-8 所示。

图2-3-8　单位冲激信号的频谱（密度）

利用相关性质可以证明，如 2-3-8（a）所示的梳状函数的频谱

式（2-3-11）表明，周期单位冲激串的傅立叶变换仍为冲激串，且强度和间隔都为。图 2-3-9（b）所示为周期单位冲激串的频谱，周期单位冲激串信号常称为梳状函数。

图2-3-9　单位冲激串的波形和频谱图

关于傅里叶级数和傅里叶变换还有以下两点说明：

（1）傅里叶级数和傅里叶变换在数学上都要求f(t)满足一定的条件。所幸的是，可物理测量的信号一般都能满足这些条件。

（2）指数形式的傅里叶级数和傅里叶变换得到的频谱图均为双边谱，其中，负的频率是没有物理意义的，这是由于引入复正弦波引起的。