连续非周期信号的傅里叶变换

现实世界中的信号通常为连续非周期信号，假设f(t)为一连续非周期信号，则傅里叶级数不能适用。但在2.1节中知道，非周期信号可以看作周期T趋于无穷大的周期信号，这样，此时离散谱线之间的间距ω0趋于无穷小（用无穷小量dω表示），在此极限下，离散频率变量kω0变为连续频率变量ω，离散求和运算符号“∑”需改为连续求和运算（积分）符号“∫”，于是式（2-3-2）可改写为式（2-3-5），这就是非周期信号f(t)的傅里叶变换（FT）。

式（2-3-5）表明：非周期信号f(t)可以分解成无穷多个指数函数ejωt之和，它占据从−∞到＋∞的全部频率域，指数函数ejωt分量的系数为。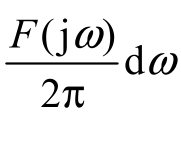

F(jω)可由信号f(t)得到，即

通常，式（2-3-6）称为傅里叶正变换［由时域f(t)求频域F(j)ω］，并记为FT[f(t)]，式（2-3-5）称为傅里叶反变换［由频域F(j)ω求时域f(t)］，记为IFT[F(j)ω]。式（2-3-5）和式（2-3-6）合称傅里叶变换对。(www.xing528.com)

注：连续形式的傅里叶变换其实是傅里叶级数的推广，因为积分其实是一种极限形式的求和算子而已。

另外，由于指数函数ejωt的系数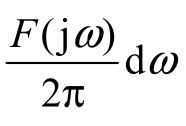是一个无穷小量，此时再用幅度表示大小就不合适了，虽然各频谱幅度无限小，但相对大小仍有区别，因此引入频谱密度的概念来表示其大小。顺便指出，在本书后面针对非周期信号讨论问题时，也常把频谱密度简称为频谱，这时在概念上不要把它和周期信号的频谱相混淆。