信号的运算方法探析

在信号的传输与处理过程中，往往需要对信号进行变换。这些变换用电子元器件实现，并且可以用相应的信号运算表示。信号的运算包括相加、相乘、平移、反转、尺度变换、微分、积分、卷积和相关等。

1.相加或相乘

两信号相加或相乘得到的新信号在任意时刻的信号值等于两信号在该时刻的信号值之和或积。

歌声与背景音乐的混合就是信号叠加的实例。通信系统中抽样、调制和解调过程中遇到的两信号相乘就是信号相乘的典型应用。

2.平移、反转与尺度变换

将f(t)的自变量更换为t+t0（t0为正或负数），则f(t+t0)相当于f(t)波形在t轴上的整体平移，当t0>0时，波形左移，当t0<0时，波形右移。平移运算也称为移位、时移或时延运算。在通信系统中，长距离传输电话信号时，可能听到回波，这就是幅度衰减的话音延时信号。

将f(t)的自变量更换为−t，此时f(−t)的波形相当于将f(t)以t=0为对称轴反转过来。反转运算也叫反褶运算。

将f(t)的自变量t乘以正实系数 a，则信号f(at)将是f(t)波形的压缩（a>1）或扩展（a<1）。这种运算称为时间轴的尺度变换。

若f(t)代表已录制声音的磁带，则f(−t)表示磁带倒转播放产生的信号，而f(2t)是磁带以二倍速度播放的声音信号，则表示原磁带播放速度降至一半产生的信号。

信号f(at+b)（式中a≠0）的波形可以通过对信号f(t)的平移、反转（a<0）和尺度变换获得。虽然对三种运算的次序没有要求，但一般情况下，为了更好地画出这类信号的波形，最好先平移，然后再反转，如果反转后再进行平移，由于这时自变量为−t，故平移方向与前述相反。

需要特别注意的是，平移、反转和尺度变这三种运算都是针对独立的、单一的自变量 t而言的，而不是对 at 或at＋b进行的。

【例2-2-1】已知信号f(t)的波形如图 2-2-9（a）所示，试画出f(−2t+4)的波形。

图2-2-9　例2-2-1图

解：f(−2t+4)是f(t)的时移、反转和尺度变换的综合。可通过三种不同的顺序得到f(−2t+4)的波形。这里介绍最常用的方式：先平移，然后反转，最后尺度变换。

（1）将信号f(t)左移，得到f(t+4)，如图 2-2-9（b）所示。

（2）进行反转，得到f(−t+4)，如图 2-2-9（c）所示。

（3）最后进行尺度变换，得到f(−2t+4)，如图 2-2-9（d）所示。

3.微分和积分

信号f(t)的微分运算是指f(t)对 t 取导数，即。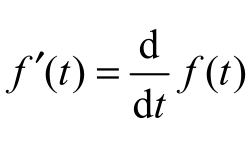

信号f(t)的积分运算是指在(−∞,t)区间内的定积分，其表达式为。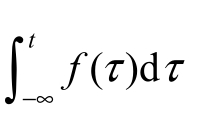

图2-2-10和图2-2-11分别表示微分运算和积分运算的例子。由图2-2-10可见，信号经微分后突出显示了它的变化部分，信号变化越快，输出越大（微分是“求变”运算）。在图2-2-11中，信号经积分运算后其效果与微分相反，信号的突变部分可变得平滑（积分是“求和”运算），利用这一作用可削弱信号中混入的毛刺（噪声）的影响。

图2-2-10　微分运算

图2-2-11　积分运算

4.卷　积

在连续信号与系统的时域分析中，卷积积分是一个重要的数学工具，它是一种特殊的积分运算，起源于信号的分解，而应用于系统对信号的响应，通常将卷积积分简称为卷积。

设f1(t)和f2(t)是定义在区间(−∞，+∞)上的两个连续时间信号，将积分定义为f1(t)和f2(t)的卷积，记为

式（2-2-15）中，τ为虚设积分变量，积分的结果为另一个新的时间信号；符号“*”表示做卷积积分运算，不表示相乘。(https://www.xing528.com)

从定义不难看出，卷积运算涉及信号的反转、平移、相乘和积分四种运算。同时，卷积运算还具有以下性质，利用这些性质可使卷积运算简化。

1）性质 1：卷积的代数性质

卷积运算满足三个基本代数运算律，即

（1）交换律：x1(t)*x2(t)=x2(t)*x1(t)

（2）结合律：x1(t)*[x2(t)*x3(t)]=[x1(t)*x2(t)]*x3(t)

（3）分配律：x1(t)*[x2(t)+x3(t)]=x1(t)*x2(t)+x1(t)*x3(t)

2）性质 2：x(t)与冲激信号的卷积

（1）任意x(t)与冲激信号δ(t)进行卷积，其结果等于x(t)本身，即

（2）任意x(t)与冲激信号的移位δ(t−t0)进行卷积，其结果是在每个冲激的位置上产生一个x(t)的镜像，即

3）性质 3：卷积定理

卷积定理包括时域卷积定理和频域卷积定理。

若信号f1(t)的频谱为F1(j)ω，信号f2(t)的频谱为F2(j)ω，则

f1(t)*f2(t)↔F1(jω)F2(jω)

f1(t)f2(t)↔F1(jω)*F2(jω)

卷积定理揭示了时域与频域的对应关系，即一个域中的卷积（积分运算）对应于另一个域中的乘积（代数运算）。例如，时域中的卷积对应于频域中的乘积。在信号和系统分析过程中，利用相应的卷积定理可以大大简化卷积的运算量。

需要说明的是，这一性质对 Laplace（拉普拉斯）变换、Z 变换、Mellin（梅林）变换等各种傅里叶变换的变体同样成立。

5.相　关

所谓“相关（relativity）”就是相似，相关分析就是分析两个不同信号间的相似性，或一个信号经过一段延迟后自身的相似性。前者称互相关分析，后者称自相关分析。由于相关大小与两信号相对位置有关。因此，相关函数表征了两信号在不同时刻的相关程度，从而在时域上揭示信号间有无内在联系。相关分析是信号处理基本方法之一。

实信号f1(t)和f2(t)，如为能量有限信号，其互相关函数定义为

可见，互相关函数是两信号之间时间差τ的函数。需要注意，一般R12(τ)≠R21(τ)。不难证明，它们间的关系是

如果f1(t)和f2(t)是同一信号，即f1(t)=f2(t)=f(t)，这时无须区分R12(τ)与R21(τ)，用R(τ)表示，称为自相关函数，即

容易看出，对自相关函数有R(τ)=R(−τ)。可见，实函数f(t)的自相关函数是时移τ的偶函数。

又因为信号f1(t)和f2(t)卷积的表达式为

为了便于与互相关函数相比较，将式（2-2-22）中的变量t与τ互换，可将信号f1(t)和f2(t)的互相关函数写为

比较式（2-2-22）与式（2-2-23）可知，卷积积分和相关函数的运算方法有许多相同之处。两种运算的不同之处仅在于：卷积运算开始时需要进行反转运算，而相关运算则不需反转。

在实际应用中，自相关在信号检测中具有重要作用，是在误码最小原则下的最佳接收准则。例如，在信号分析与处理过程中，常常利用自相关从强噪声中检测弱的周期信号；互相关在车速测量、直线定位，以及模式识别和密码分析学领域中都有应用。