常见的典型信号分类及应用场景

1.正弦信号

正弦信号的函数表达式为

式（2-2-1）中，A 为信号的振幅，ω是角频率（rad/s），0φ为初相位（rad），这三个参量称为正弦信号的三要素。

正弦信号是一种周期信号，其周期T与角频率ω及频率 f 之间满足以下关系：

由于余弦信号与正弦信号只是在相位上相差 π/2，因此在电学中，将它们统称为正弦信号。

在信号分析中，常将信号分解为一系列正弦信号的移位加权和，这是因为正弦信号是比原信号更加简单的信号，而且具有原信号所不具有的特性——频率保持性，即一个正弦信号输入线性时不变系统后，输出仍是正弦信号，只有幅度和相位可能发生变化，但频率和波形仍是一样的，而且只有正弦信号才拥有这样的性质，正因为如此，信号分析中常用正弦信号表示原信号而不用方波或三角波来表示。

2.复指数信号复指数信号的函数表达式为

式（2-2-3）中，s 为一复数，即s=σ+jω。利用欧拉公式e±jωt=cosωt±jsin ωt，式（2-2-3）可表示为

可见，一个复指数信号可分解为实部和虚部两部分，两者均为实信号，而且是频率相同、振幅随时间变化的正（余）弦振荡信号。s的实部σ表征了该信号振幅随时间变化的状况，虚部ω表征了其振荡角频率。若σ<0，则是衰减振荡［见图 2-2-1（a）和（b）］；若σ>0，则是增幅振荡［见图 2-2-1（c）和（d）］；若σ=0，则是等幅振荡。当ω=0，复指数信号就成为实指数信号Aeσt。如果σ=ω=0，则为直流信号。可见，复指数信号概括了许多常用信号。

图2-2-1　复指数信号示例

复指数信号是一个抽象的信号，实际中并不存在复指数信号（均为实信号），但借助于复指数信号，可以把直流信号、实指数信号、正弦信号以及增长或衰减的正弦信号（或称为指数包络正弦信号）统一到同一个形式，从而描述幅值、频率、相位和衰减等特征量，加之复指数信号的微积分仍然为一个复指数信号，给信号分析、计算带来了很大的方便，因此得到了广泛应用。

另外，借助欧拉公式，正弦信号和余弦信号可表示成复指数信号形式，即

3.门信号

门信号的函数表达式为

从式（2-2-6）可知，f(t)是一个高度为 1，宽度为τ的矩形脉冲信号，如图 2-2-2 所示。

图2-2-2　门信号

4.奇异信号

在信号分析中，经常遇到以下两种情况：一种是某信号在空间或时间坐标上集中于一点（如物理学中的质点、面积趋于零的压强、脉宽趋于零的电脉冲），另一种情况是信号本身有不连续点（跳变点）或其导数有不连续点的情况。这时普通函数的概念就不够用了，而用单位冲激信号和单位阶跃信号就很方便。为了区分普通函数，一般将冲激信号和阶跃信号称为奇异信号。

单位阶跃信号的函数表达式为

从式（2-2-7）可以看出，t<0时信号为零；t>0时接入信号；t=0处没有定义，是信号的突变点，信号从零值突变到单位值，如图2-2-3所示。

图2-2-3　单位阶跃信号

单位阶跃信号可作为理想开关的模拟函数。例如，信号v(t)=12u(t)，这个信号在t<0时为零；t>0时等于 12 V。此时，单位阶跃信号就相当于一个12 V 电源的开关。因此，单位阶跃信号u(t)又可称作开关信号。

利用单位阶跃信号的单边性，可用其表示单边信号、有范围限制的信号等。

单位冲激信号又称为冲激函数，最初是由狄拉克提出并定义的，因此又称为狄拉克δ函数，记为δ(t)，函数表达式为

式（2-2-8）中的两个部分是一个整体，必须同时满足，如图 2-2-4 所示。其中，冲激函数在无穷区间上的积分面积称为冲激函数的强度，将单位冲激函数乘以常数 A，就得到冲激强度为 A 的冲激函数，记为Aδ(t)。

为了更好地理解单位冲激信号，单位冲激信号可以看成是由门信号（矩形脉冲）取极限得到。如图 2-2-5 所示，门信号的宽度是τ，高度是1/τ，面积为 1。保持面积 1 不变，当脉冲宽度减小，其高度将增大，当脉冲宽度趋于无限小时，其高度将趋于无限大，当脉冲宽度趋于零时，此极限情况下的脉冲信号就是单位冲激信号。

图2-2-4　单位冲激信号(www.xing528.com)

图2-2-5　门信号演变为单位冲激信号

可见，单位冲激信号是一种持续时间无穷短、瞬间幅度无穷大、涵盖面积恒为1的理想信号。虽然冲激信号较为抽象，但其物理意义确实存在，如物理学中的质点问题、受力面积趋于零时的压强问题，以及电学中的抽样脉冲、雷击、电闪等问题，这些问题均不是连续分布于空间或时间中，而是集中在空间中的某一点或者时间中的某一瞬时，当引入冲激信号的概念后，问题的解决就会很方便。

需要说明的是，δ(t)不能用经典数学中“任意给定 t，存在确定的δ(t)”的方法定义，原因是δ(0)为无穷大，而无穷大不是确定值，因此δ(t)不是普通函数，属于广义函数的范畴，为了便于应用，在叙述中不强调数学上的严谨性，只强调使用和运算方便。

单位冲激函数具有如下性质。

1）性质 1：δ(t)是偶函数

即

2）性质 2：取样性

设x(t)为连续时间信号，且在t=t0处连续，则

式（2-2-10）表明，若要从连续时间信号x(t)中抽取任一时刻的函数值x(t0)，只要乘以冲激信号δ(t−t0)并在区间(−∞,∞)上积分即可，或者说冲激信号可以把冲激所在位置的函数值抽取出来。

3）性质 3：冲激函数和阶跃函数互为微分和积分关系

冲激函数为阶跃函数的微分，即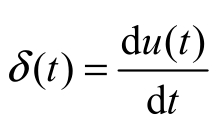

阶跃函数为冲激函数的积分，即

4）性质 4：用δ(t)信号可表示任意信号f(t)

如图 2-2-6 所示，对任意信号f(t)，可以分成很多宽度为τΔ的矩形脉冲，其中第k个脉冲出现在t=kτΔ时刻，其强度（矩形脉冲的面积）为f(kΔ)ττΔ，用冲激函数可表示为f(kΔτ)Δτδ(t−k Δτ)。

图2-2-6　用冲激信号表示任意信号

这样，可以将f(t)近似地看作由一系列强度不同、接入时刻不同的窄脉冲组成，所有这些窄脉冲的和近似等于f(t)，即

当Δτ→0时（用无穷小量dτ表示），式（2-2-11）中kτΔ由离散量变为连续量（用τ表示），∑（离散和）要改为积分∫（连续和），“≈”改为“＝”。即

综上所述，可得到如下重要结论：任意信号x(t)可以用经平移的无穷多个单位冲激函数加权后的连续和（积分）表示。换言之，任意信号x(t)可以分解为一系列具有不同强度的冲激函数的移位加权和。这是信号时域分析的基本思想。

在信号分析过程中，还经常用到由单位冲激函数派生出的梳状函数。梳状函数的定义式为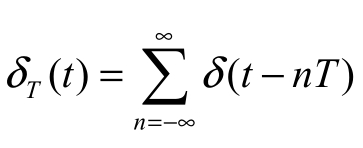，其时域波形是周期为 T 的单位冲激串，所以也称为理想抽样函数，其波形如图 2-2-7 所示。

图2-2-7　梳状函数的波形

6.抽样信号

抽样信号用符号Sa(t)表示，其数学表达式为

抽样信号的波形如图2-2-8所示。

图2-2-8　Sa（t） 函数

从图 2-2-8 可以看出，Sa(t)信号是一个偶函数，在t=0处取得最大值，在t =±π,±2π…±mπ时函数值等于零（即等间隔过零点），在t的正、负两方向振幅都逐渐衰减。

与Sa(t)信号类似的是sinc(t)信号，它的表达式为