梯级水库群拦沙计算模型优化

4.3.2.1 模型建立的基础

由于梯级水库群数量众多、空间拓扑结构复杂以及水库运行方式多样，目前采用精确的水沙数学模型进行大范围水库群的拦沙计算还存在困难，而采用Brune[41]拦沙率、Vörösmarty[42]流域水库群综合拦沙率等方法是可行的估算手段。

4.3.2.2 单一水库拦沙计算

1.基本公式

对于单个水库拦沙计算采用Brune拦沙率公式：

其中

上二式中：TE为水库的拦沙率，%；Δτ为水库滞水系数；C为水库淤积剩余库容，m3；I为水库年入库径流量，m3。

Brune拦沙率公式最早是根据美国40余座水库的淤积资料得到，后期在其他国家的水库拦沙计算中发现其依然可以提供较好的拦沙计算结果。

由于水库在拦沙过程中库容不断减少，由Brune拦沙率公式可知其拦沙率TE也在不断降低，因而，在运用该公式对单个水库长期拦沙计算时需要考虑水库拦沙量的年际变化。

2.计算验证

采用Brune拦沙率公式对已建水库的拦沙率进行计算，计算值和实测值见表4.3-3，计算得到的拦沙率与实测值较为吻合，验证了模型的可靠性。进一步对溪洛渡、乌东德水库进行拦沙计算，并与“九五”和“十一五”水沙数学模型计算结果[30，43]对比，计算结果吻合较好（表4.3-4），拦沙率最大误差仅为2.57%。

表4.3-3　长江上游部分已建大型水库拦沙率计算值与实测值对比

表4.3-4　长江上游部分在建、拟建水库拦沙率计算结果对比

4.3.2.3 梯级水库群拦沙计算

以单一水库Brune拦沙计算方法为基础，理论上可以建立梯级水库群拦沙计算方法。为减少运算量、降低复杂程度，研究中常对其进行简化。Vörösmarty提出流域水库群综合拦沙率方法[42]，计算公式如下：(www.xing528.com)

以上式中：Ci为第j个子流域第i个水库的库容，m3；n j为第j个子流域的水库个数；I j-mouth为第j个子流域最末一级水库的入库径流量，m3；Δτj为第j个子流域的滞水系数；TE j为第j个子流域的拦沙率，%；m为子流域个数；I mouth为全流域最末一级水库的入库径流量，m3；TE basin为全流域水库群的拦沙率，%。

假设某流域上游为弱产沙区，中下游为强产沙区，在流域水库群总库容一定的条件下，设定两种水库分布情况：①绝大部分水库分布在上游，少数水库分布在下游；②少数水库分布在上游，绝大部分水库分布在中下游。以上两种情况下，水库群实际拦沙效果后者大于前者，而Vörösmarty方法对两种情况的计算结果相同，无法反映这一差异，与实际情况不符。

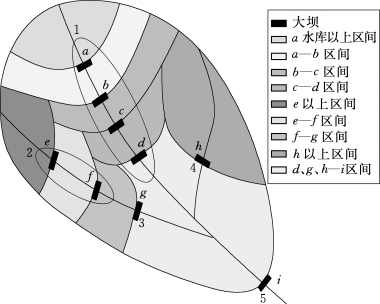
图4.3-2　水库分组范例

鉴于此，本研究提出分组拦沙率，在对水库群分组的基础上进行拦沙计算，以充分考虑水库分布和强产沙区分布对计算的影响。分组时遵循以下规则：①组内各水库空间位置相邻且处于弱产沙区；②拟建水库分组时投产时间须一致；③控制性水库原则上列为组内最末一级。以图4.3-2中的水库分组情况（5组）为例，对计算方法进行说明。

将图4.3-2中的水库群按上述原则分为5组后，等价于将其视为5个水库进行计算，在保证计算精度的前提下，简化了运算。各水库组拦沙计算时，与Vörösmarty方法类似，即将组内水库集中至最末一级水库处进行计算，各水库组拦沙率计算公式如下：

上二式中：j为水库组编号，TEj为第j组水库的拦沙率，%；Δτj为第j组水库滞水系数；Cj为第j组水库的淤积剩余库容，m3；I j为第j组水库最末一级入库径流，m3。

由各水库组的拦沙率，结合入库沙量，即可计算拦沙量，计算公式如下：

式中：Sj为第j组水库的拦沙量，t；SYj为第j组水库的入库沙量，t；其他符号意义同上。

由于上游水库对下游水库的入库沙量存在制约，故需自上至下依次迭代计算各水库组的入库沙量（以上一级水库组的出库沙量加上区间来沙量，作为下一级水库组的入库沙量）。以图4.3-2为例，各水库组的入库沙量计算公式如下：

其中：SSYd、SSYf、SSYf-g、SSYh、SSYd，g，h-i分别为d以上、f以上、f-g、h以上、d，g，h-i区域的输沙模数，t/km2；A d、A f、A g、A h、Ai分别为水库d、f、g、h、i的控制流域面积，km2；其他符号意义同上。

依据上述方法，采用1961—1970年水沙序列对乌东德和白鹤滩水库联合运行后综合拦沙率进行计算，并与相关单位水沙数学模型计算成果[43]进行对比，与水沙模型结果吻合较好（表4.3-5），拦沙率最大误差为1.55%。

表4.3-5　乌东德和白鹤滩水库综合拦沙率计算结果对比