热交换器优化设计简介

热交换器的优化设计，就是要求所设计的热交换器在满足一定的要求下，一个或数个指标达到最好。经验证明，一个好的设计，往往能使热交换器的投资节省10%～20%。许多工厂离不开热交换器，一个炼油厂，热交换器的投资竟达到全部工艺设备投资的40%左右，因此，“经济性”常常成为热交换器优化设计中的目标。在优化方法上，把所要研究的目标，如“经济性”，称为目标函数，其目的就是要通过优化设计，使这个目标函数达到最佳值，亦即达到最经济。由于实际问题的要求不同，如有的设计要在满足一定热负荷下阻力最小；有的要求传热面最小等等，因而就有不同的目标函数。

任何一个优化设计方案都要用一些相关的物理和几何量来表示。由于设计问题的类别或要求不同，这些量可能不同，但不论哪种优化设计，都可将这些量分成给定的和未给定的两种。未给定的那些量就需要在设计中优选，通过对它们的优选，最终使目标函数达到最优值，我们把这些未定变量称为设计变量。如，以热交换器的传热系数为目标函数的优化设计，流体的流速、温度等就是设计变量。这样，对于有n个设计变量x1，x2，…，xn的最优化问题，目标函数F（X）可写作

F(X)=F(x1,x2,…,xn)

显然，目标函数是设计变量的函数。最优化过程就是设计变量的优选过程，最终使目标函数达到最优值。最优化问题中设计变量的数目称为该问题的维数。设计者应尽量地减少设计变量的数目，把对设计所追求目标影响比较大的少数变量选为设计变量，以便使最优化问题较易求解。

在优化设计过程中，常常对设计变量的选取加以某些限制或设置一些附加设计条件，这些设计条件称为约束条件。如求解热交换器传热性能最好的问题，常常有阻力损失不能超过某个数值的约束条件。约束条件可分为等式约束条件和不等式约束条件。在某些特殊情况下，还会有无约束的最优化问题。最优化问题的求解可以是求取目标函数的最小值，或求取目标函数的最大值。一般情况下，习惯上都是求取目标函数的最小值，所以，对于求取F（X）的最大值问题应转化成求取相反数-F（X）的最小值问题。如，求取热交换器传热系数最大的问题就是求取传热热阻最小的问题。

这样，最优化问题的一般形式可表达为

minF(X)

约束条件

hi(X)=0 (i=1,2,…,m)

gj(X)≤0 (j=1,2,…,l)

式中，X=[x1，x2，…，xn]T，表示为一个由n个设计变量所组成的矩阵（角码T为矩阵的转置）。hi（X）及gj（X）分别表示i个等式约束及j个不等式约束条件。在上式所表达的最优化问题中，根据F（X）、h（X）和g（X）与变量X之间的函数关系不同及变量X的变化不同，可分为不同类型的最优化问题，因而其数学求解的方法也不同。热交换器优化设计问题一般都是约束（非线性）最优化问题（也可称为约束规划问题）。约束最优化问题的求解方法有消元法、拉格朗日乘子法、惩罚函数法、复合形法等多种，读者可参阅有关优化方法的书籍来了解这些方法。

今以热交换器的设计来考虑经济性问题为例来讨论设计的最优化。设一台热交换器的投资费用为B[RMB¥/台]，它的使用年限为n年，亦即折旧率为，而输送热交换器中流体所需能耗费用为A[RMB¥/yr]，则考虑了这些因素的热交换器的经济指标φ可表示为

现在要求设计出来的热交换器为最经济，即这是一个minF（X）=minφ的最优化问题。固然可以把上式中的A、B等量当做设计变量，但是它们不能直接反映出与热交换器设计中密切相关的一些几何量与物理量，所以应该进一步对A、B等量作一分析。

已知传热的基本方程式为

对于热力系统中的一台热交换器，流体的进、出口温度及所需传递的热量Q一般都已被工艺流程的要求所决定，平均温差Δtm可认为差别不大，则传热面积F成为仅是传热系数K的函数。在确定了某种结构类型的热交换器前提下，K值与传热面的具体布置等有关，要由设计者确定。

如果忽略热交换器金属壁的热阻，并且不考虑污垢热阻，则传热系数K为

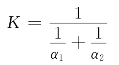
设该热交换器为翅片管式，管内为热水，管外为空气，则对于管内强迫对流换热α1可用式

求解。对于管外的空气横掠翅片管对流换热的α2可用式

求解。根据准则的定义知，及，结合以上各式，可将传热面积F 表示为如下的函数形式：

F=f(w1,w2,d,ρ1,ρ2,λ1,λ2,μ1,μ2,cp1,cp2)(www.xing528.com)

因为流体的进出口温度已经给定，它们的热物性参数λ、ρ、μ、cp等可视为常数。为了使问题简化，如也给定某种管径d，则

F=f(w1,w2)

即传热面积的大小由两侧流体流速所决定。据统计，热交换器的金属材料费用占热交换器费用的50%以上，即金属材料费用的多少决定了热交换器的投资费用的增减，而金属消耗量又主要决定于传热面积，所以，我们可以把设备投资与传热面积关联起来。亦即从传热角度看，增大流速，可使传热面积减少，相应的也就降低了热交换器的投资费用B。

但是从输送流体的能量消耗观点来看，恰恰相反。流速的增加，必然使阻力增加。因为由式（6.17）可见，在忽略气体加速产生的附加阻力及浮力引起的内阻力情况下，两侧流动阻力为

Δp1=Δpf1+Δp11=f(w1)

Δp2=Δpf2+Δp12=f(w2)

阻力的增加意味着输送流体的能耗费用A亦增加。

由上分析可见，对于所给定的条件，两侧流体流速w1及w2是决定设备投资费用B与能耗费用A的关键性参数。流速的选择是否恰当，将直接影响热交换器的设计是否合理，从而影响经济指标φ，所以也可称这种参数为“经济性参数”。

为了使问题进一步简化，对于所设计的热交换器还可从两侧流速中分析出影响最大的一侧流速。今为气-液热交换，可以认为主要热阻在空气侧，而且水与能耗的关系不如空气时那样显著，也就是说矛盾的主要方面是在空气侧，因而可仅将空气的流速w2作为经济性参数。这样，通过以上分析与简化得出，该优化设计为以空气流速w2为设计变量的一维无约束优化（严格说，应为约束优化，因风机功率有限，阻力损失总有一定限度），即

minF(X)=minφ(w2)

如果我们知道了φ（w2）这一具体的函数关系式，就可用一维搜索方法来求解。为了避免应用最优化的数学方法，下面我们采用图解法来说明这一优化过程。

对所需设计的热交换器选取一系列不同的流速w2，并由传热计算求得相应所需要的一系列传热面积F，从而由传热面的单位造价bRMB¥/m2求得总造价B，即

B=bF,RMB¥

再由用户提出的使用年限n确定折旧率η′%，这样即可求得流速w2与折旧费η′B的关系曲线η′B=f（w2）。

另外，根据不同流速w2可求得相应阻力值Δp，并求得相应的功率消耗

如果每年运行时间为τ（h），电费为S[RMB¥/（kW·h）]则能耗费用为

A=NτS,RMB¥/yr

所以也可求得每年的运行费用A与流速w2的关系曲线A=ξ（w2）。

将两条曲线绘于同一图上，进行叠加，即得φ-w2的曲线。此曲线的最低点的流速为最佳流速（即最优化点），相应的经济指标φ值即为最优值（见图6.13）。

按照上述所讨论的情况，某单位曾对3200m3/h的全低压制氧装置中的液空过冷器进行了分析计算。设电费S=7×10-2RMB¥/（kW·h），制造费用单价b=400 RMB¥/m2，折旧率=10%，则得最佳流速w2=2.5m/s。式（6.22）中的每一个量给定为不同值时都会引起最佳流速的变化，如，经计算当电费降到S=3×10-2RMB¥/（kW·h），设折旧率η不变，则空气最佳流速增大到3m/s。当折旧率η上升时（即使用年限缩短），设提高到η=50%，则空气最佳流速增大到3.5m/s。

应该指出，对于上例的热交换器优化设计，只考虑空气流速为设计变量是不够完善的。一般，还应从以下这些量中选择若干个作为设计变量：管长，管径，翅片高，翅间距，工质出口温度，设备安装费，工质（如水）费用等。当然，设计变量越多，寻求最优化的过程越复杂，计算工作就越大。但是，随着计算技术的发展，解决热交换器设计的优化已不成问题。用电子计算机进行热交换器的设计，将会大大节省人力，并能获得令人满意的结果。

近年来，一些先进的优化方法被引入到热交换器的优化设计中，如，模糊优化设计。它可以根据人们对换热器的设计要求达到“重量轻，换热效率高、压降小”这种多目标、但又无确切边界的“模糊”的问题，运用结构模糊优化理论来寻求目标相对地达到最优。模糊优化的具体方法有多种，由于实际工程的复杂性，目前模糊优化设计还应用得很少，但这是应值得关注的新方法。

图6.13 经济指标与流速的关系