汽-水喷射式热交换器的优化设计

1）构造与工作原理

汽-水喷射式热交换器的喷管多做成渐缩渐扩喷管，混合室为圆筒形，如图4.19所示。压力po的工作蒸汽，从位于混合室前某一距离的喷管中绝热膨胀后，以很高的流速wp喷射出来，卷吸周围的被引射水。当蒸汽和水的温差足够大的时候，可认为蒸汽在进入混合室之前完全被凝结在被引射水中，同时使被引射水温从th提高到tg。在混合室入口处，水的速度场很不均匀，经过混合室使混合水的流速得到均衡，达到w3，并使压力从混合室入口压力p2升到混合室出口压力p3，再经过扩散管，混合水压力升高到pg流出。

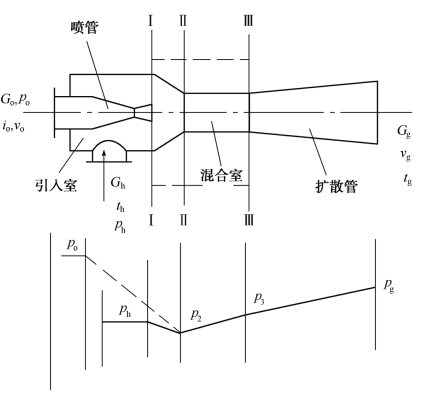
图4.19 汽-水喷射式热交换器工作原理

2）特性方程式

对于图4.19中用虚线围起来的那部分来说，质量守恒方程式与能量守恒方程式与式（4.32）、式（4.33）相同，但对汽-水喷射器，能量守恒方程式（4.33）还可写成：

式中 c——水的比热，kJ/（kg·℃）；

th——在喷射器前被引射水的温度，℃；

tg——在喷射器后混合水的温度，℃。

动量方程式可写成如下形式：

式中 wp——工作蒸汽在喷管出口处的流速，m/s；

wp=φ1(wp)a

（wp）a——绝热流动的蒸汽速度，m/s；

wh——喷管出口截面上，被引射水流过环形截面处的流速，m/s；

w3——混合室出口截面上混合水的流速，m/s；

fp——喷管出口截面积，m2；

fh——被引射水流通过喷管出口截面处的环形截面积，m2；

f3——圆筒形混合室的截面积，m2；

pp——喷管出口工作蒸汽的绝对压力，Pa；

ph——被引射水在引入室的绝对压力，Pa；

p3——混合室出口处混合室的绝对压力，Pa；

φ1、φ2——考虑到流体在喷管和混合室中流动时存在摩擦而引起的能量损失，称速度系数。

为简化特性方程式的推导，可作如下假定：

（1）由于fh相对很大，可认为wh≈0；

（2）喷管出口压力pp等于引入室中水的压力ph；

（3）Ⅰ—Ⅰ截面的截面积（fp+fh）比圆筒形混合室截面积（f3）大很多，因此被引射水的压力从ph降到p2是在靠近混合室的进口处达到的。故可认为，Ⅰ—Ⅰ截面和Ⅱ—Ⅱ截面之间作用于混合室入口段的圆锥形壁面上的冲量积分为

将上述假设代入式（4.35），并考虑u=Gh/G0，可得

又，水在混合室出口处的流速

混合室出口处混合水的绝对压力为

式中 vg——混合水的比容，m3/kg；

pg——扩散管出口混合水的绝对压力，Pa；

φ3——扩散管的速度系数。

喷管出口处的蒸汽流速：

式中 ip——蒸汽在喷管出口处的焓，kJ/kg。

由热力学可知，蒸汽通过缩扩喷管的最大流量

式中 f1——喷管喉部的截面积，m2；

k——绝热指数；

p0——蒸汽进入喷管前的绝对压力，Pa；

v0——蒸汽进入喷管前的比容，m3/kg。

将式（4.37）～（4.40）代入式（4.36），经过整理之后可得到汽-水喷射式热交换器的特性方程式为

式中 A——常数，对于干饱和蒸汽，k=1.135，则A=0.202。

pg-ph=Δpg，为蒸汽-水喷射式热交换器产生的压力差即扬程，Pa。

根据经验数值，推荐φ1=0.95，φ2=0.975，φ3=0.9。又若用于采暖供热系统中，可认为vg=vh=0.001m3/kg，在这种情况下，上式成为

当然，若不是用在采暖供热系统，则不能作这样的简化，特性方程仍为式（4.41）。

3）极限工作状态及其计算

在汽-水喷射式热交换器中，喷射系数过小或过大都不能保证喷射器的正常工作。具体地说，在喷射系数过小时，水温可提高到混合室压力相应的饱和温度，这样就会由于没有足够的水来凝结进入的蒸汽而使喷射器的工作遭到破坏，这个状态决定了最小喷射系统umin。在喷射系数过大时，被引射水的流量过多，混合室中的水温要降低；同时混合室中水的流速增大，而水的压力要降低。当被引射水的流量增加到一定值时，混合室入口截面上的压力p2要降到被加热水温tg相对应的饱和压力pb，而引起混合室中水的沸腾，这个状态决定了最大喷射系数umax。只有p2大于tg所对应的饱和蒸汽压力pb时，混合室中的液体才会流动，随后在混合室中将压力提高到p3，并在扩散管中将水的压力提高到pg。因此在设计一个喷射器时，应该检验其喷射系数是否在umin和umax的范围之内。至于umin与umax的大小可用下述方法来确定。

混合水温tg可由能量守恒方程（4.34）得到

据此可用饱和蒸汽表确定与它相对应的饱和蒸汽压pb。

圆柱形混合室始端水压p2取决于被引射水由于工作蒸汽和被引射水之间的动量交换而获得的速度。假使认为工作蒸汽凝结后，形成以很高速度流动且其所占截面积很小的工作液体流束，以及这股流束和被引射水的动量交换是在圆柱形混合室中进行，那么就可忽略在压力ph下被引射水所具有的平均速度。在这样的情况下，混合室始端水的压力可用伯努利方程来确定：

式中 φ4——混合室入口段的速度系数，一般φ4=0.925；

vh——被引射水的比容，m3/kg。

混合室入口处水的流速w2值为

将式（4.45）代入式（4.44）可得

通过喷管的流量G0也可写成

于是

以k=1.135，vh=0.001m3/kg代入时，则有

根据式（4.43）和式（4.49），可以求出不同喷射系数时的tg和p2，以及与tg相对应的饱和压力pb。将p2=f（u）以及pb=f（u）绘于同一图上时，它们的交点即表示umax和umin，具体解法可见例4.2。

4）喷射器几何尺寸的计算

喷管临界直径d1可由下式计算：

式中 v1——蒸汽在喷管中处于临界压力时的比容，m3/kg；

i1——蒸汽在临界压力时的焓，kJ/kg。

喷管的出口面积

喷管出口直径

式中 vp——蒸汽在喷管出口压力Pp时的比容，m3/kg。

喷管渐扩部分的长度

其中θ为扩散角，一般为6°～8°。

关于圆筒形混合室的直径d3，可由求出的截面比加以确定，其中f1为喷管的临界截面积，该值为

圆筒形混合室之长Lh，一般取Lh=（6～10）d3。

扩散管的扩角θ，一般也取6°～8°，其出口直径d4一般与供水干管相同。

[例4.2]^[3]1在一蒸汽喷射取暖系统中，要求汽水喷射热交换器的设计参数如下：

热负荷Q=502.8×104kJ/h；

供水温度（即喷射器出口温度）tg=95℃；

回水温度（即被引射水的温度）th=70℃；

系统和管路压降（即喷射器扬程）Δpg=78.48kPa；

引水室的绝对压力ph=1.96×105Pa。

试确定喷射器主要几何尺寸，并绘出它的特性曲线和确定极限工况。

[解]

1）蒸汽喷射器的设计参数试取进喷射器的饱和蒸汽参数为：绝对压力p0=4.91×105Pa，焓i0=2749kJ/kg，比容v0=0.38m3/kg。喷射器出口的混合水量

由蒸汽喷射热水采暖系统的热平衡，可求出喷射系数

(www.xing528.com)

工作蒸汽量

被引射的水量

Gh=Gg-G0=48000-1967=46033kg/h

喷管出口蒸汽状态参数：pp=ph=1.96×105Pa，由此查水蒸气焓熵图得：ip=2589 kJ/kg；vp=0.85m3/kg；故

i0-ip=2749-2589=160kJ/kg

喷管中的临界参数：

p1=βcp0=0.577×4.91×105=2.83×105Pa

i1=2652kJ/kg; v1=0.62m3/kg

蒸汽自喷管进口绝热膨胀至临界状态时的焓降为

i0-i1=2749-2652=97kJ/kg

按以上所得的喷管中的状态参数做成的示意图如图4.20所示。

2）求蒸汽喷射器的截面比（f1/f3）

将有关参数代入特性方程式（4.42），并加以整理后得

求得两根，即截面比：

图4.20 例4.2的水蒸气的焓熵图

其中第一个根是不合理的，故取。

3）计算喷射器的主要尺寸

由式（4.50）计算喷管的临界直径

由式（4.52）计算喷管出口直径

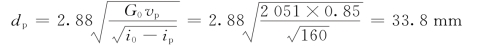
取扩散角θ=8°，则由式（4.53）计算喷管扩散段长度

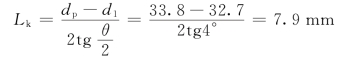
由于，于是

圆筒形混合室直径

混合室长度，取Lh=8d3=8×68.1=545mm

4）蒸汽喷射器特性曲线的绘制

当室外气温变化时，必须调整工作蒸汽的压力p0和进汽量G0，以适应负荷的变化，因而应针对不同负荷绘制特性曲线。

（1）当室外气温低于设计气温时，供热负荷将要增加，若供热负荷增加为Q1=1.15Q，将蒸汽绝对压力提高到p01=5.89×105Pa，从蒸汽表查得

i01=2757kJ/kg v11=0.32m3/kg

喷管喉部参数：

p11=0.577×5.89×105=3.4×105Pa

i11=2661kJ/kg v11=0.53m3/kg

喷管出口参数：

pp1=1.06×105Pa ip1=2560kJ/kg

喷汽量

将上述有关参数代入喷射器特性方程（4.42），即可得到p01=5.89×105Pa时的特性方程：

（2）在设计工况下的特性方程，根据第2）项的计算，应为

（3）当室外气温高于设计气温时，供热负荷将减小，假设供热负荷降低到Q2=0.8Q，此时将工作蒸汽的绝对压力降低到p02=3.92×105Pa，从蒸汽表查得

i02=2740kJ/kg v02=0.47m3/kg

喷管喉部参数：

p12=0.577 p02=2.26×105Pa i12=2644kJ/kg v12=0.77m3/kg

喷管出口参数：

pp2=1.96×105Pa ip2=2623kJ/kg

喷汽量

将有关参数代入特性方程式（4.42），并经整理后得

Δpg=5.98×104-10.5(1+u)2,Pa (c)

以不同的u值，代入（a）、（b）、（c）三式，可得到三种不同进汽压力下的Δpg值，计算结果列于表4.3。

表4.3 不同进汽压力时的Δpg、Vg与u的关系

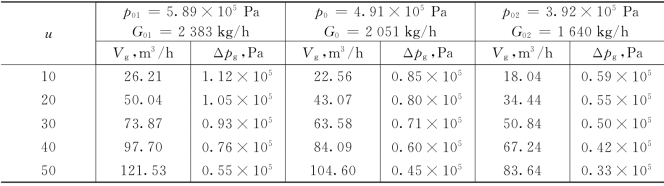
以扬程Δpg为纵坐标，以u为横坐标，则可构成Δpg=f（u）曲线，如图4.21所示。

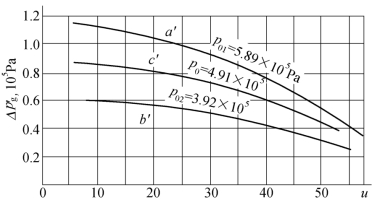
图4.21 蒸汽喷射器的Δpg=f（u）曲线

5）喷射器的喷射系数

不同进汽压力下在不同的u值时喷射器出口处水的容积流量（即热水供暖系统循环水量）Vg，按下式计算：

Vg=0.001(1+u)G0,m3/h

计算结果也列于表4.3内。根据表中数据，绘出Δpg=f（Vg）曲线，如图4.22。该图中还绘出了网路阻力特性曲线Δpg=SV2g。根据本例所给数据Vg=48 m3/h，Δpg=0.7848×105Pa，故S值为

图4.22 蒸汽喷射器的Δpg=f（Vg）曲线

故Δpg=34.1V2g。喷射器在不同汽压力下运行时，它所产生的扬程（即压差）Δpg应与网路阻力相一致。因此图4.22上a、b、c三个交点的纵坐标分别表示所产生的扬程。其值分别为1.03×105Pa，0.54×105Pa，0.785×105Pa。再在图4.21上，查出与此三个值相对应的交点a′、b′、c′三点，据此可分别得到运行时的喷射系数u，结果为

当p01=5.89×105Pa时，u=23；

当p02=3.92×105Pa时，u=22；

当p0=4.91×105Pa时，u=22.4。

6）蒸汽喷射器的极限工作状态

为求极限工作状态，应根据式（4.43）求出不同u时的混合水温tg以及与tg相对应的饱和压力pb，绘出pb=f（u）曲线。再按式（4.49）求出在不同喷射系数u时混合室入口压力p2并绘出p2=f（u）曲线。从两条曲线的交点找出umin与umax，检验喷射器运行时的u值是否在它们的范围之内。为此，必须对上述三种不同进汽压力予以分别考虑。

（1）在设计工况下，喷射器的进汽参数为p0=4.91×105Pa，i0=2749kJ/kg，被引射水温th=70℃，用式（4.43）计算出不同喷射系数时的tg值，并由蒸汽表查得与tg相应的饱和压力pb，其结果列于表4.4。

（2）在热负荷增加，p01=5.89×105Pa时，i01=2757kJ/kg，G01=2383kg/h，此时可由热平衡关系求出供水系统回水温度（即被引射水温）

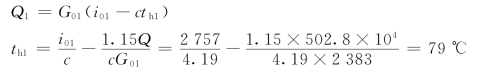
将i01及th1的值代入式（4.43）求出tg1，并查出与tg1相应的饱和压力pb1，其结果也列在表4.4。

（3）在热负荷减小，p02=3.92×105Pa时，i02=2740kJ/kg，G02=1640kg/h时，此时供热系统回水温度仍由热平衡求得

所得之tg2及pb2也列在表4.4中。

表4.4 不同u值时的tg与pb值

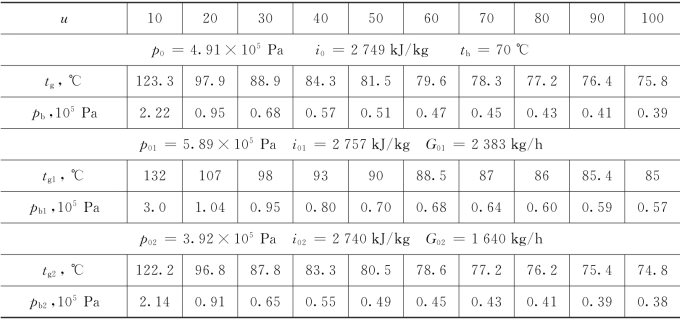
根据表4.4上所列的三组数据，分别绘出pb=f（u）曲线，如图4.23至图4.25中下面一条曲线。

为求出在不同喷射系数时的p2值，将有关参数代入式（4.49），得到不同进汽压力时计算公式如下：

（1）当p0=4.91×105Pa时，

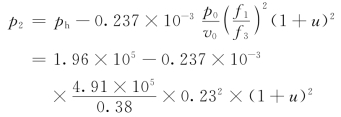
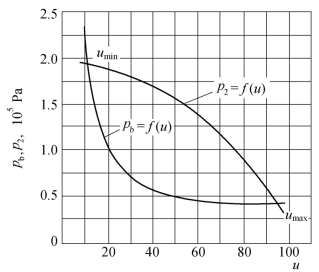
图4.23 pb-u与p2-u曲线（p0=4.91×105Pa）

（2）当p01=5.89×105Pa时，p2=1.96×105-23.1（1+u）2Pa；

（3）当p02=3.92×105Pa时，p2=1.96×105-10.5（1+u）2Pa。

以不同的u代入，所得不同情况下的p2值如表4.5所示。

图4.24 pb-u与p2-u曲线（p0=5.89×105Pa）

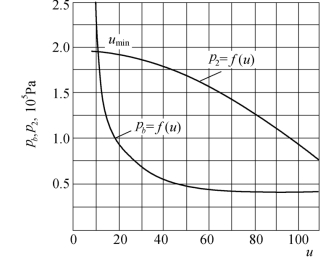
图4.25 pb-u与p2-u曲线（p0=3.92×105Pa）

表4.5 不同u值时的p2值（×105Pa）

将表中所列的p2值，绘成p2=f（u）的关系曲线，分别如图4.23至图4.25中上面一条曲线所示。

从图可见，在p0=4.91×105Pa时，umin=12，umax=95。而在此种进汽压力下运行时的u=22.4，喷射器可以正常工作。

在p01=5.89×105Pa时，umin=13，umax=76。而在此种进汽压力下运行时的u=23，故喷射器也可正常工作。

在p02=3.92×105Pa时，umin=11，umax＞110。而在此种进汽压力下运行时的u=22，故喷射器仍可正常工作。