冷水塔热力计算技巧

冷水塔的热力计算，逆流式与横流式有所不同。由于塔内热量、质量交换的复杂性，影响因素很多，很多研究者提出了多种计算方法。在逆流塔中，水和空气参数的变化仅在高度方向，而横流式冷却塔的淋水装置中，在垂直和水平两个方向都有变化，情况更为复杂。下面仅对逆流式冷水塔计算中的焓差法作一介绍。

1）迈克尔焓差方程

1925年，迈克尔（MerKel）首先引用了热焓的概念建立了冷水塔的热焓平衡方程式。利用迈克尔焓差方程和水、气的热平衡方程，可比较简便地求解水温t和热焓i，因而至今仍是对冷水塔进行热力计算时所采用的主要方法，称为焓差法，其要点如下：

取逆流塔中某一微段dZ（见图4.9），设该微段内的水、气分布均匀，进入该微段的总水量为L，其水温为t+dt，经过该微段的热质交换，出水温度为t，蒸发掉的水量为dL。进入该微段的空气量为G，气温为θ，含湿量为x，焓为i，与水进行热交换后dZ段的温度、含湿量及焓分别为θ+dθ、x+dx、i+di。

在微段内接触传热量与蒸发散热量之和为

或

式中 a——填料的比表面积，m2/m3；

A——塔的横截面积，m2；

Z——塔内填料高度，m；

x″、x——与水温t相应的饱和空气含湿量以及与水相接触的空气的含湿量，kg/kg。

将路易斯（Lewis）关系式^[1]1

α/βx=cx（cx为湿空气比热）

及含湿量为x的湿空气的焓ix=cxθ+rx，

水面饱和空气层（其温度等于水温t）的焓i″=cxt+rx″，代入式（4.5）则得

此即迈克尔焓差方程，它表明塔内任何部位水、气之间交换的总热量与该点水温下饱和空气焓i″与该处空气焓i之差成正比。该方程可视为能量扩散方程，焓差正是这种扩散的推动力。但应指出，路易斯关系式只是在特定的绝热蒸发的条件下才是一个常数，因而迈克尔方程存在一定的近似性。

图4.9 逆流式冷水塔中的冷却过程

2）水气热平衡方程

在没有热损失的情况下，水所放出的热量应当等于空气增加的热量。在微段dZ内水所放出的热为

其中c为水的比热。而空气在该微段吸收的热为

因而

式中等号右边第一项为水温降低dt放出之热，第二项为由于蒸发了dL水量所带走的热，此项数值与第一项比相对较小，为简化计算，将其影响考虑到第一项中，将第一项乘以系数1/K，因而得

此即该微段的热平衡方程。

此处有必要对系数K做一些说明：

①从上引出系数K的过程可知，它是一个与蒸发水量有关的系数，它应当小于1；

②将式（4.10）代入式（4.9），有Gdi=KGdi+ctdL

整理后成为

其中的ctdL值（即蒸发散热量）只占总传热量的百分之几，因而K≈1；

③若用式（4.10）对全塔进行积分，则有

又在淋水装置全程内，水气之间有如下热平衡：

或

将式（4.12）和式（4.13）比较后可知：

其中

可得

在炎热的夏季，接触传热量Qα甚小，故，所以

其中的汽化潜热r应取淋水装置中与水平均温度相应的数值，但它在一般的水冷却条件下变化不大，故实际计算中可用t2时的汽化潜热。从上式可见，K是出口水温t2的函数，此关系示于图4.10。

3）计算冷水塔的基本方程

综合迈克尔焓差方程（4.6）和热平衡方程（4.10），可得

(www.xing528.com)

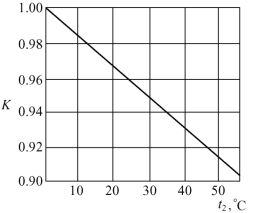
图4.10 K值与冷却水温t2的关系

对此进行变量分离并加以积分：

式（4.18）是在迈克尔方程基础上以焓差为推动力进行冷却时，计算冷水塔的基本方程，若以N代表该式的左边部分，即

称N为按温度积分的冷却数，简称冷却数，它是一个无量纲数。

再以N′表示式（4.18）右边部分，即

称N′为冷水塔特性数。冷却数表示水温从t1降到t2所需要的特征数数值，它代表着冷却任务的大小。在冷却数中的（i″-i）是指水面饱和空气层的焓与外界空气的焓之差Δi，此值越小，水的散热就越困难。所以它与外部空气参数有关，而与冷水塔的结构和型式无关。在气量和水量之比相同时，N值越大，表示要求散发的热量越多，所需淋水装置的体积越大。特性数中的βx反映了淋水装置的散热能力，因而特性数反映了淋水塔所具有的冷却能力，它与淋水装置的构造尺寸、散热性能及水、气流量有关。

冷水塔的设计计算问题，就是要求冷却任务与冷却能力相适应，因而在设计中应保证N=N′，以保证冷却任务的完成。

4）冷却数的确定

冷却数实际上就是焓差的倒数求积分，上限为进水温度t1，下限为出水温度t2。但在冷却数定义式中，（i″-i）与水温t之间的关系极为复杂，一般只能近似求解，这里介绍各种近似解法中的辛普逊（Simpson）近似积分法。此法系将冷却数的积分式分项计算求得近似解。按辛普逊积分法的要求，将积分区间分成偶数个小段，设段数为n，每个小段的水温变化值为δt/n，从而可知各小段的水温。与每个水温相应的饱和焓i″可在湿空气的温湿图（附录H）或湿空气表（附录G）上查到，与每个水温相应的空气的焓i，也可由式（4.12）写成

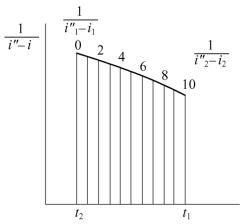
图4.11 辛普逊积分法求冷却数

的形式，把它计算出来。

于是，就可得到与每个水温相对应的1/（i″-i）值，并将它们绘成以t为横坐标，以1/（i″-i）为纵坐标的点，然后以每三个点即0、1、2，2、3、4，4、5、6，…抛物线连接（如图4.11），于是用辛普逊积分的结论，可得出t2-0-10-t1所包围的面积为

而冷却数为

由式（4.21）可知，后一个等分的in与前一个等分的in-1值的关系为

在计算时，应从淋水装置底层开始，先算出该层的i值，再逐步往上算出以上各段的i值。各段的K值也应根据相应段的水温按式（4.16）计算。

若对精度要求不高，且δt＜15℃时，常用下列两段公式简化计算：

式中 ——与水温对应的饱和空气焓，kJ/kg；

i1、i2——分别为空气进口、出口处的焓，kJ/kg；

δt——水在塔内的温降，℃。

而 。

5）特性数的确定

为使实际应用方便，常将式（4.20）定义的特性数改写成

式中 βxV——容积传质系数，βxV=βxa，kg/（m3·sΔx）；

V——填料体积，m3。

可见特性数取决于容积传质系数、冷水塔的构造及淋水情况等因素。

6）换热系数与传质系数的计算

在计算冷水塔时要求确定换热系数和传质系数。假定热交换和质交换的共同过程是在两者之间的类比条件得到满足的情况下进行，由相似理论分析，换热系数和传质系数之间应保持一定的比例关系。此比例关系与路易斯关系式的结果一致。

在冷水塔计算中，cx一般采用1.05kJ/（kg·℃）。

由此可得到一个重要结论：即当液体蒸发冷却时，在空气温度及含湿量的实用范围变化很小时，换热系数和传质系数之间必须保持一定的比例关系，条件的变化可使某一个增大或减小，从而导致其他一个也相应地发生同样的变化。因而，当缺乏直接的实验资料时就可根据上述比例关系予以近似估计。

可以说直到现在为止，还没有一个通用的方程式可以计算水在冷水塔中冷却时的换热系数和传质系数，因此更有意义的是针对具体淋水装置进行实验，取得资料。图4.12和图4.13示出了由试验得到的两种填料的βxV曲线^[2]1。图4.14则是已经把不同气水比（空气量与水量之比，以λ表示）整理成与特性数之间的关系曲线，图中示出了两种填料的特性，更多的资料可见参考文献[2]、[8]等。

7）气、水比的确定

图4.12 塑料斜波55×12.5×60°-1000型容积传质系数曲线[8]

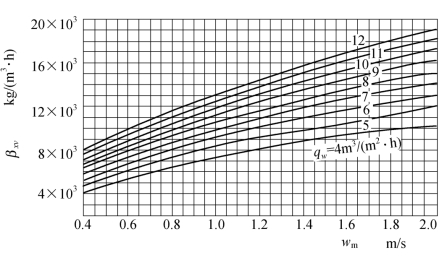
图4.13 纸质蜂窝d20，H=10×100=1000型容积传质系数曲线[8]

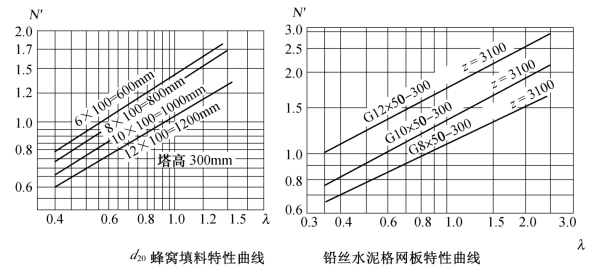
图4.14 两种填料的特性曲线[7]

气、水比是指冷却每公斤水所需的空气公斤数，气、水比越大，冷水塔的冷却能力越大，一般情况下可选λ=0.8～1.5。

由于空气的焓i与气、水比有关，因而冷却数也与气、水比有关。同时特性数也与气、水比有关，因此要求被确定的气、水比能使N=N′。为此，可用牛顿迭代法上机计算或者在设计计算中假设几个不同的气、水比算出不同的冷却数N，作如图4.15所示的N～λ曲线。再在同一图上作出填料特性曲线N′～λ曲线，这两条曲线的交点P所对应的气、水比λP就是所求的气、水比。P点称为冷水塔的工作点。

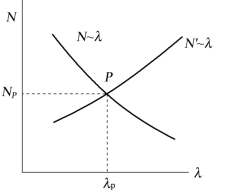
图4.15 气、水比及冷却数的确定