板翅式热交换器设计计算

1）几何尺寸计算

首先应根据所给定的工作条件，包括热负荷、允许压降、流体特性、有无相变、温差大小、最高工作压力等因素，选定翅片型式和规格，然后才可进行以下的计算。

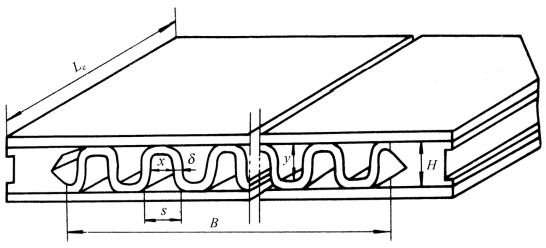
图3.44 板翅基本单元的结构尺寸图

图3.44为板翅基本单元的结构尺寸图。其中：H——翅片高；δ——翅片厚度；s——翅片间距，s=x+δ；Le——单元的有效长度；B——单元的有效宽度；x——内距，x=s-δ；y——内高，y=H-δ。

（1）当量直径de

（2）通道的自由流通面积A

对于每个（层）单元，通道的自由流通面积为

n层板束的通道的自由流通面积

（3）传热面积

n层通道的一次传热面积

n层通道的二次传热面积

n层通道的总传热面积

2）翅片效率和翅片表面总效率

（1）翅片效率

图3.45（b）表示板翅式热交换器中冷、热两流体之间热量传递通过翅片及隔板的情况及翅片表面上的温度分布。由隔板直接传递的热量Q1通过隔板表面传给流体，它可表示为

式中 α——隔板表面与流体间对流换热系数；

F1——一次传热面积，指隔板表面的传热面积；

tw——隔板表面温度；

tf——流体温度。

沿翅片传入的热量Q2，将通过翅片表面与流体之间对流换热而传给流体，它可表示为

式中 α——翅片表面与流体间的对流换热系数，可认为与式（3.40）中α值相同，因而两式中的α在符号上没有加以区别；

F2——二次传热面积，指翅片表面的传热面积；

tm——翅片表面的平均温度。

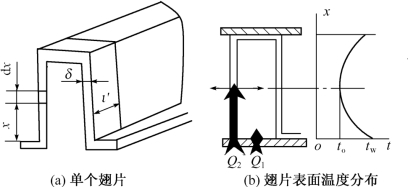
图3.45 翅片及其表面温度分布示意图

由图3.45（b）可见，在热流体向冷流体传热的冷流体通道中，翅根温度（亦即隔板表面温度）tw高于翅片中心处表面温度to，这时翅片表面的平均温度tm必然是tw＞tm＞to。如果将式（3.41）中的tm用tw来代替，则式（3.41）可改写为

式中 ηf——翅片效率。

将式（3.40）与式（3.42）比较可见，如果把二次传热面的传热温差看做和一次传热面的传热温差相等，都为（tw-tf），就需要将二次传热面的面积打一个折扣，即乘上二次传热面的翅片效率ηf。实质上，这是由于二次传热面的表面平均温度tm低于一次传热面表面温度tw所致。

令式（3.41）与式（3.42）相等，即得

由式（3.43）可见，翅片效率的意义表示了翅片的实际传热量（在翅片表面平均温度tm下）和理想的最大可能传热量（在翅根温度tw下）之比。在数值上，它等于二次传热面的实际平均温差和一次传热面的传热温差之比值。

今任取距翅根x处的一微元段dx，讨论在dx段上的热平衡关系[图3.45（a）]。因为翅片很薄，它的厚度远小于翅片高度，并且它是金属，导热系数很大，所以可以忽略沿翅片厚度方向的温度梯度。即假定只有沿翅高x方向温度才有显著变化，而任一截面上各点的温度被认为与截面的中心温度一致。这样，热传导就只发生在沿x方向。对于微元段dx而言，设在x截面上由热传导导入热量为Qx，在x+dx截面上由热传导导出热量为Qx+dx。同时，它还因对流通过翅表面向周围传热（即传给周围流体）Qc。则在热稳定状态下，存在着热平衡关系：

根据傅里叶定律可写出

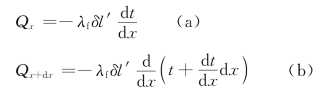
式中 λf——翅片的导热系数；

l′——沿流体流动方向的翅片长度。根据对流换热公式有

式中 α′——同时考虑了对流和垢阻后的复合换热系数，即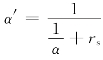，假设它沿翅片表面为常数，其中的rs为翅片表面污垢热阻；

t——金属翅片的温度。

将以上（a）至（c）式代入式（3.44）得

假定周围流体的温度tf为常数，并设

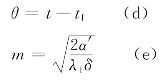
则式（3.45）成为

将边界条件代入式（3.46）的通解中求得：

由上式可见，运行中沿翅片高度（即x方向）的温差是变化的，则沿整个翅高的平均温差可由上式按中值定理求得，即

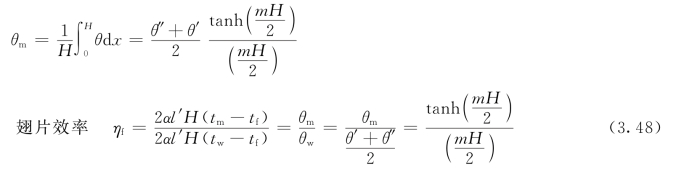
式中，θm为翅片的平均温度与流体温度的温差；θ′、θ″分别为翅片始端和末端对周围流体的温差；θw为翅根的温度与流体间的温差，由于翅两端（即两根部）均向翅中部传热，故翅根温差可按两端部温差平均计算，即为双曲正切函数。式（3.48）中的H，实质上应该是代表二次表面热传导的最大距离，也就是说这是传热问题中所用的一个“定型尺寸”。为了避免简单地把定型尺寸误解为就是翅高H，所以给予它符号为b，则翅片效率按式（3.48）可通用性地表示为

式中b的数值应该随冷、热通道的不同排列而不同，图3.46～图3.48表示了通道中的传热具有对称性时三种不同排列情况下的b值。当通道传热近似对称时，为了简化计算也可近似地用这一方法决定b值。

图3.46 冷热通道间隔排列

图3.47 两个热通道之间隔两个冷通道b1=H1；b2=H2

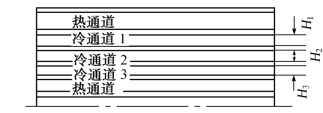
图3.48 两个热通道之间隔三个冷通道

显然，对于两股流的板翅式热交换器，当一个热通道与冷通道间隔排列时，因根部温差对称，定型尺寸应为。

由式（3.43），式（e）及式（3.49）等可以看到影响翅片效率的因素有：

①翅片定型尺寸b越小，或翅高H越低，则热阻越小，tm→tw，翅片效率ηf就越高，所以单叠布置（指一个冷通道与一个热通道间隔排列）的翅片效率高于复叠布置（指两个冷或热通道间隔几个热或冷通道的排列）。

②翅片越厚，热阻越小，tm→tw，ηf就越大。

以上两点可综合为：翅片低而厚，则ηf高；翅片高而薄，则ηf低。

③翅片与流体间的换热系数越小，则沿翅片表面的散热量也越小，tm→tw，ηf就越大。

④翅片材料的导热性能越好，即λf越大，tm越接近于tw，ηf就越高。

通过翅片效率的分析及前述翅片型式的介绍可以看到，对于翅片的选择上首先应作翅片型式选择，再确定其几何参数。综合起来，翅片的选择应根据最高的工作压力、传热能力、允许压力降、流体性能、有无流体的相变及冷、热两流体对流换热系数大小等因素考虑。翅片的类型依流体的性能和设计使用的条件等来选定，当流体之间温差较大时，宜选用平直翅片，温差较小的情况选用锯齿形翅片；若流体的黏度较大，如油等，宜用锯齿形翅片以增加扰动；如在流体中含有固体悬浮物时，宜选用平直翅片；如在传热过程中有相变的冷凝、蒸发等情况，宜选用平直或多孔翅片。在空分设备中，可逆式热交换器大多选用锯齿形翅片，既强化气流放热，又便于水分和二氧化碳的析出和清除，而冷凝蒸发器（主冷器）大多采用多孔翅片，以避免杂质结晶的局部集结和破坏冷凝膜的边界层。为了有效地发挥翅片的作用，使其有较高的翅片效率或传递较多的热量，在对流换热系数大的场合，往往选用低而厚的翅片；而在换热系数小的场合，选用高而薄的翅片为宜。当参加换热的两种流体的换热系数相差悬殊时，除了采取上述措施外，还可以采取换热系数小的一侧A用两个通道，而换热系数大的一侧B用一个通道，即AABAABAAB…的复叠布置形式。

（2）翅片壁面总效率

对于两股流的热交换器，当一个热通道和一个冷通道间隔排列时，它们之间的传热量为式（3.40）所示的Q1和式（3.42）所示的Q2之和，即

因此，可以写出一个以总传热面积F=F1+F2为基准的传热方程式

所以

其中，η0称为翅片壁面总效率。其值为

因

所以

分析式（3.51）可见，翅片壁面总效率的物理意义是，把二次传热面和一次传热面同等看待，认为都处于一次传热面的传热温差（tw-tf）下时，对总传热面所应打的折扣。由此所得的传热面积，也称为有效传热面积Fe，即

分析式（3.53）可见，翅片壁面总效率η0必大于翅片效率ηf。而且，翅片效率越高，则壁面总效率也就越大。图3.49表示了翅片壁面总效率和翅片几何参数及换热系数的关系。

图3.49 翅片壁面总效率和翅片几何参数及换热系数的关系

当流体A的一个通道与流体B的两个通道间隔排列，即以ABBABBABB…排列时，翅片表面总效率的计算式与冷、热流体通道一一间隔时就有所不同。通过类似分析，对两个B通道而言可以得出

式中 ——一半一次传热面（即F1/2）的效率；η2——二次传热面的翅片效率。(www.xing528.com)

上式可理解为当两个通道排列在一起时（如B通道）的一次传热面，有一半（即两个B通道之间的一次传热面）其传热情况相当于二次传热面，需要乘以效率η′1。

由式（3.56），可设，则得

η1为两个B通道排在一起时，B通道的总的一次传热面的效率。η′1、η1和η2可由以下关系式计算：

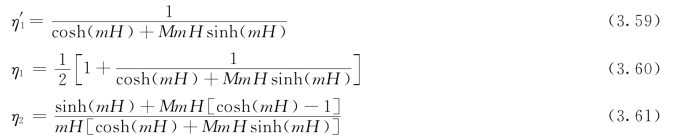
式中 。

当忽略MmHsinh（mH）和MmH[cosh（mH）-1]，且H=b时，则以上三式成为

比较式（3.64）和式（3.48）可见，两者形式相同，所不同的只是，当忽略上述两项时它们所取的定型尺寸不同，前者为H/2，而后者为H。

3）传热量和传热系数的计算

板翅式热交换器中冷、热流体的传热方程式按照式（3.51）的关系可以表示为

式中 Qc、Qh——分别为壁面对冷流体的放热量和热流体对壁面的放热量；

αc、αh——分别为冷、热流体与壁面间的换热系数；

Fc、Fh——分别为冷、热流体通道总传热面积；

η0c、η0h——分别为冷、热流体通道翅片壁面总效率；tfc、tfh——分别为冷、热流体温度；

tw——壁面温度。

在稳定传热情况下，Qc=Qh=Q，并忽略翅片及隔板热阻，将式（3.65）与式（3.66）变换相加可得

由于在热交换器中，流体的温度通常是沿流程变化的，所以根据第一章中所述原理，可以将式（3.67）中两流体温差取为对数平均温差Δtlm，则得

或

式中 Kc、Kh——分别为以冷、热通道总传热面积为基准时的传热系数。

关于对数平均温差Δtlm，仍由关系式Δtlm=Ψ·Δtlm，c计算，修正系数Ψ可从本书第一章或其他参考资料中查取。

当比热发生很大变化时，如在压力为4MPa的情况下，空气在主热交换器中随温度的降低，比热将变化数十倍，这时应该用第一章中所述的积分平均温差代替对数平均温差，否则，将会引起较大误差。

在乙烯装置、全低压空分装置和其他石油化工装置的板翅式热交换器中，常有多股流换热的传热过程。例如，对于用三种冷流体来冷却裂解气，则可把这三种冷流体综合成一股相当的返流气体，并按下式计算其传热系数：

式中 Kf——正流侧裂解气的传热系数；

αf——正流侧裂解气的换热系数；

η0f——正流侧翅片壁面的总效率；

Ff——正流侧通道的总传热面积；

αr——返流侧平均换热系数；

η0r——返流侧平均壁面总效率；

Fr——返流侧通道的总传热面积。

对于冷、热流体都是多股流时的传热系数及多股流时平均温差Δtm的求解，请参阅参考文献[8]及其他有关文献。

4）换热系数的计算

（1）无相变时的对流换热系数

对于板翅式热交换器，无相变时的对流换热系数通常用传热因子j与雷诺数Re的关联式来求取。即

故

式（3.73）的具体形式因翅片的类型和结构参数不同而异，通常都由实验建立线图或整理成相应的关联式。图3.50为日本神钢“ALEX”的几种翅片性能曲线，该曲线只区别翅片类型而不区分其尺寸。参考文献[18]的作者提出，该曲线的数据可靠，也适用于我国生产的大部分翅片，而且可拟合成下列关联式：

锯齿翅片（Re=300～7500）

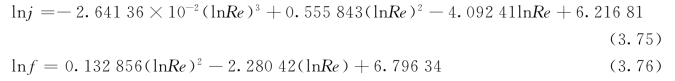
多孔翅片（Re=400～10000）

lnj=34.57583-15.92678(lnRe)+2.136707(lnRe)2-9.544151×10-2(lnRe)3(3.77) lnf=28.79806-12.31399(lnRe)+1.565191(lnRe)2-6.736098×10-2(lnRe)3(3.78)

平直翅片（Re=400～10000）

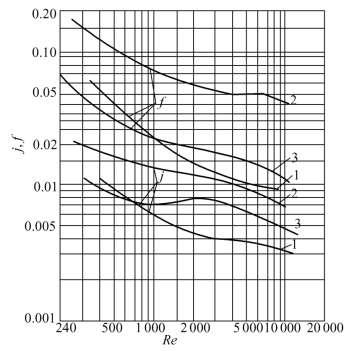
图3.50 日本神钢“ALEX”的几种翅片性能曲线

1-平直翅片，2-锯齿翅片，3-多孔翅片

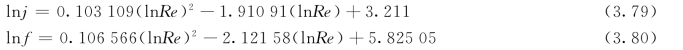
式中 f——摩擦因子。

（2）有相变时的换热系数

这方面的研究工作还很不够，现综合有关资料，提出如下一些用于相变换热的关联式，供读者选用参考。

①冷凝换热[20]

当液膜为层流时，凝结换热系数为

当液膜为紊流时

式中 Rel——液相雷诺数；

γ——汽化潜热，kJ/kg；

q——热流密度，W/m2。

②沸腾换热

核态沸腾时，沸腾换热系数为

式中 ρ——操作（绝对）压力，N/m2；

σ——液体表面张力，N/m；

cpl——液体定压比热，kJ/（kg·K）；

cs——金属校正系数：钢、铜为1.0，不锈钢、铬、镍为0.7；磨光表面为0.4。

5）压力损失计算

在板翅式热交换器中造成流体流动的阻力有多处，为了简化这种计算，可以把板翅式热交换器分成入口端、出口端和中心部分三个部分来分别计算所造成的压降（图3.51）。

（1）热交换器芯子入口的阻力 该阻力是由于导流片出口到翅片入口的流通截面变化而造成的：

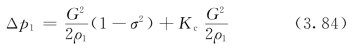
式中 Δp1——入口处压力降，N/m2；

ρ1——入口处流体密度，kg/m3；

G——流体在板束中的质量流速，kg/（m2·s）；

σ——板束中该流体通道的自由流通面积与横截面积之比；

Kc——收缩阻力系数（查参考文献[8]）。

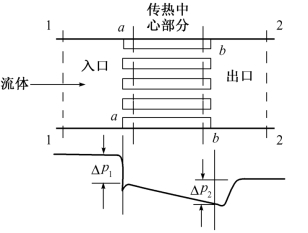
图3.51 板翅式热交换器芯子中的进口压降和出口压升

（2）热交换器芯子出口的阻力 该阻力是由于翅片出口到导流片入口的流通截面变化而引起的：

式中 Δp2——出口的压力回升，N/m2；

ρ2——出口处流体密度，kg/m3；

Ke——扩大阻力系数（查参考文献[8]）。

（3）热交换器芯子中的阻力 它主要由传热面形状的改变而产生的阻力和摩擦阻力组成：

式中 f——摩擦因子（参考图3.50）；

L——热交换器芯子长度（即通道长度），m；

de——通道当量直径，m；

ρm——流体平均密度，，kg/m3

总的压力降Δp即为三者之和：

在板翅式热交换器设计中，在多股流的情况下，还应对通道的排列进行合理的安排，以免出现类似于管壳式热交换器中温度交叉现象及热量内耗（如，热流体A和冷流体B、C的换热都安排在同一台热交换器中，如果通道排列布置成…ABCABCABC…，冷流体B、C间将发生换热，其结果是影响了传热面的有效使用，这是设计者所不希望的，称之为热量内耗）。