流程组合与传热、压降计算

1）流程组合

为了满足传热和压力降的要求，对于板式热交换器可进行多种方式的流程和通道数的配置：①流体的流动可以是串联、并联（这时形成纯逆流）和混联（如图3.16（c），一种流体为并联，而另一种流体为串联）。②流程可以是单流程或多流程，两流体的流程数可以相等或不相等。③两流体的流程中通道数不一定要相等[如图3.16（c）中，一种流体为1（程）×4（通道），另一种流体为2（程）×2（通道）]。

板式换热器内流程与通道的配置方式常以下列数学形式表示：

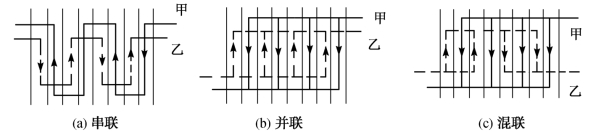
图3.16 流体的流动连接

其中，M1，M2，…，Mi——从固定压紧板开始，热流体侧流道数相同的流程数；

N1，N2，…，Ni——相应于M1，M2，…，Mi流程中的流道数；

m1，m2，…，mi——从固定压紧板开始，冷流体侧流道数相同的流程数；

n1，n2，…，ni——相应于m1，m2，…，mi流程中的流道数。

图3.17表示了流程组合的实例，其中横线上方（1×4）表示甲流体为单流程、四通道，横线下方（2×2）表示乙流体为两流程、两通道。由该图可见：①通常板片四角都开孔，但在实现流程换向（即不是单流程）的板片上应有不开孔的情况，即存在“盲孔”。此外，在两端的端片上也有盲孔。②对于“单边流”的板片，如果甲流体流经的角孔位置全在热交换器的左边，则乙流体所流经的角孔位置应在热交换器的右边。同理，“对角流”的板片（如本例），甲流体如流经一个方向的对角线的角孔位置，乙流体应流经另一方向的对角线的角孔位置。

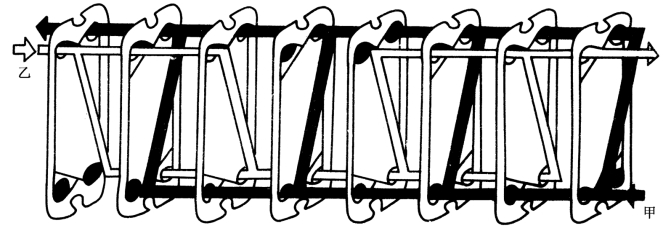
图3.17 板式热交换器的流程组合示意图

2）传热计算

传热计算的基本方程仍是传热方程式，所要注意的是，由于板片的角孔及密封垫片等处并不参与传热，板片又是波纹形的，板式热交换器的传热面积应该是扣除不参与部分后板片的展开面积，即有效传热面积。

平均温差Δtm的计算为按纯逆流情况下对数平均温差值Δtlm，c再乘以修正系数Ψ，即

Δtm=Δtlm,cΨ

根据参考文献[4]，Ψ值的确定，在串联和并联时可用图3.18，混联时可采用管壳式热交换器的温差校正系数。MarriottJ[6]提出在两侧体积流量比为0.7～1及NTU值不超过11时的温差修正系数图（图3.19）。BuonopaneR等[5]提出了求解的数学模型，在作某些假设和简化的前提下，求解结果与此图中值极为接近。根据传热单元数NTU=KF/Wmin及热流体与冷流体的流程数，即可由此图求得相应的对数平均温差修正系数Ψ值。

传热系数K的计算，在已知两侧对流换热系数及垢阻条件下，仍用以往常用的公式，即

式中，δ与λ分别为板片厚及其导热系数；r1、r2为板片两侧的污垢热阻。板式热交换器由于流动中的湍动较大，故比较不易结垢，其污垢热阻要比一般的管壳式小。参考文献[21]汇集了在多种情况下板式热交换器中的污垢热阻值，如表3.2所示。

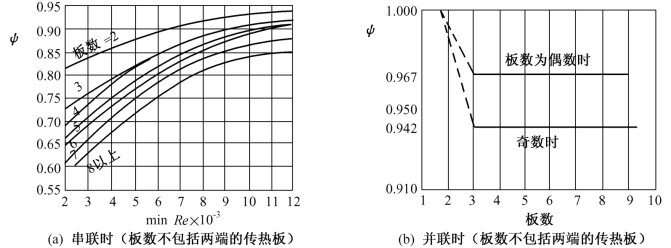
图3.18 板式热交换器的温差修正系数（LMTD法时）

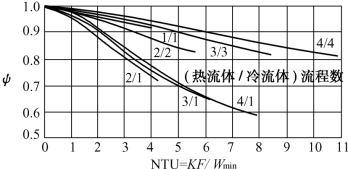
图3.19 温差修正系数（NTU法时）

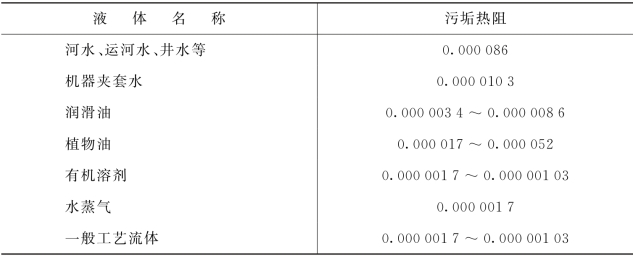
表3.2 板式热交换器中的污垢热阻值[21]单位：m2·℃/W

续表3.2

对流换热系数α1及α2的计算，一般在无相变情况下板片两侧都将保持传热相似，所以α1及α2均可按同样的公式计算，如传热不相似则需分别用各自的公式计算。

板式热交换器放热计算的基本公式形式与管内或槽道内的对流换热计算公式相同，湍流换热时为

当流体被加热时，m=0.4；被冷却时，m=0.3。其中的C、n值随板片、流体和流动的类型不同而不同。

参考文献[6]对上式中系数和各指数提出了这样的范围：C=0.15～0.4，n=0.65～0.85，m=0.3～0.45，Z=0.05～0.2（指黏度修正项上的指数）。这些数值可供读者在进行试验研究整理准则关系式时及选用时参考。

对牛顿型流体的层流换热，可用Sieder-Tate型式的方程式[7]，即

式中 C=1.86～4.50；n=0.25～0.33；x=0.1～0.2，通常为0.14。

在计算板式热交换器流道内流体的Re值时，所采用的当量直径de可按下式计算：

式中 Lw——板有效宽；

h——波纹深度；

b——板间距。（参考图3.9（b）及3.9（c））

当板片两侧冷热流体的流通截面不等时，应按其实际的流通截面A及热周边U来分别计算板片两侧流道的当量直径。

在有相变时，板式热交换器内流体的相变换热系数计算很复杂，何种计算方法最为可靠尚未得到公认。本书作者通过科研、综合与分析，现提出一些计算式供读者参考。(www.xing528.com)

蒸汽凝结换热系数的计算，应按不同的凝结区运用相应的计算式。对于重力控制区（Relf＜临界雷诺数，约为150～500），可用下列较为简易的关联式求解凝结换热系数，即

式中，

λl——凝液导热系数，W/（m·℃）；

αc——凝结换热系数，W/（m2·℃）；

Relf——凝液膜雷诺数，，

qm为凝液质量流率，kg/s；L为板片通道宽，m。

对于剪切力控制区（Relf＞临界雷诺数），则为

式中，Rel——出口处凝液雷诺数，

G——气-液混合物的总质量流速，kg/（m2·s）；

xo——出口处蒸汽干度；

H——考虑凝液膜厚度影响的无因次参数，H=CpΔT/γ′；

γ′——考虑凝液过冷和液膜对流换热影响的参数，J/kg，

γ′=γ(1+0.68CpΔT/γ)

γ——汽化潜热，J/kg；ρl、ρg——分别为凝液及进口处蒸汽密度，kg/m3；

Prl——凝液的Pr数。

——密度比，考虑蒸汽压力的影响。

关于板式蒸发器中的沸腾传热，通常可认为是以环状流为主，则其沸腾换热系数αb可利用分液相时的对流换热系数αl与强化因子Fb的积来计算，即

式中，αl可按式（3.19）计算，其中的；Fb按下式计算

式中，为两相流因子，称为摩阻分液相表观系数，无因次量。其定义为

式中，（Δpf）tp为两相流的摩擦阻力；（Δpf）l为仅液相单独流过同一管道时的摩擦阻力。

3）压力损失计算

国内制造厂家对于板式热交换器用于无相变换热时的压力降计算通常是以欧拉数Eu与雷诺数Re之间的准则关系式给出的：

式中的系数b和指数d随板式热交换器的具体结构而定，指数d应为负值。

由Eu=Δp/ρw2，可求得多程时的压降为

式中，m为流程数；w为工质在流道中的流速，m/s。

在计算板式热交换器压降时的Re值时，当量直径de应按下式计算：

若板片两侧的流通截面不等，则应按其实际的流通截面A及湿周边U来分别计算两侧流道的当量直径。

计算压降的准则关系式中Re数前相乘的系数及Re数的指数随板型不同其差异很大。同时，在实际运行中由于板片两侧流道的压力不等，两流道间压差较大时可能引起板片的较大变形。此外，不同的流程、角孔组成的通道内的阻力等都使得实际运行中的压力降和厂方所推荐的计算式有较大差异，所以这种计算式只能提供用户在较理想情况下选用参考。

对于板式冷凝器或板式蒸发器，其中的冷凝侧或沸腾侧中流体的流动为两相流，阻力计算很复杂，在此提出如下一种经本书作者研究所得的简易计算，供读者参考。

板式冷凝器的总压降Δp与流道中气-液两相流的混合平均雷诺数之间存在如下关系：

式中c为有量纲（Pa）的系数，c与指数n随不同板型而异，由实验确定。有关这一详细计算及其他计算方法，可参阅参考文献[19]及[26]。