简介：流路分析法的应用

贝尔法的缺点是烦琐、费时，不过这个问题在应用计算机后就可解决了。实际上此法并未把各流路的关系完全考虑在内，因此无法预测由于制造条件或结构等因素引起的各路流量及其相应阻力的变化，虽可作进一步改进，但总的近似程度还不如流路分析法好。

流路分析法是利用廷克所提出的将壳程流动分成如图2.40所示的五股流路，将图中每一流路设想为一条管路，如此则使折流板前后的流动状况构成一个如图2.40所示的管路网络图，图中的箭头和字母表示各流路的流动途径，符号K表示阀门，代表流动阻力。由图可见，当流体流过前一块折流板的缺口后，在横流经过管束的进口处，流体将分成C、B、E等三股并联流路，它们平行地流过两折流板之间的空间，在管束出口处又汇合在一起，然后经过折流板缺口处进入下一段管束。至于A和D，则可设想它们从两块折流板之间的某一点，平行地流到下一块折流板空间的对应点汇合。

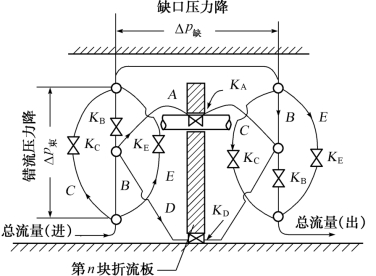
图2.40 壳程各流路的管路网络图

按并联管路的原理，应有

式中Δp束为两折流板缺口之间的错流压力降，Δp缺为通过缺口处的压力降。

根据质量守恒，总流量MS应为各分流量之和，即

每一流路的压力降为

(www.xing528.com)

式中 Δpj——各流路的压力降，Pa；

kj——各流路的阻力系数；

wj——各流路的流速，m/s；

ρs——流体的密度，kg/m3。

Mj与wj的关系为

式中 Sj——各流路的流通截面积，m2。

当已知kj、Sj时，则可由式（2.65）～（2.68）解出各路流量，亦即可通过上述方程式定量地解决各流路的相互关系。但应用于实际计算中要定量算出各路流量，往往还需要有缺口处压降Δp缺的计算式，其解决方法如下：

缺口处流量应有

定义缺口面积后，若已知缺口阻力系数k缺，即可用式（2.68）、式（2.69）的关系确定Δp缺。所以已知6个阻力系数kj（包括k缺）后，可由6个方程式定量地解决各流路的相互关系。至于各流路的阻力系数kj，是与有关结构参数及雷诺数有一定关系的，一般要对各流路进行单独试验加以确定。