如何计算换热系数

1）管内、外换热系数

在考虑换热系数时，虽然可从某些参考资料上查考，但由于它受众多因素的影响，还是通过公式计算比较可靠。

流体流过各种形式壁面时的换热系数，一般是在试验基础上，把它的变化规律用努塞尔准数（Nu）或传热因子（jh）与雷诺数（Re）之间的关系用公式或线图的形式表示出来。Nu、Re的定义为

至于jh，要注意有科恩（Kern）传热因子和柯尔本（Colburn）传热因子之分，其定义分别为科恩传热因子

柯尔本传热因子

两者之间的关系

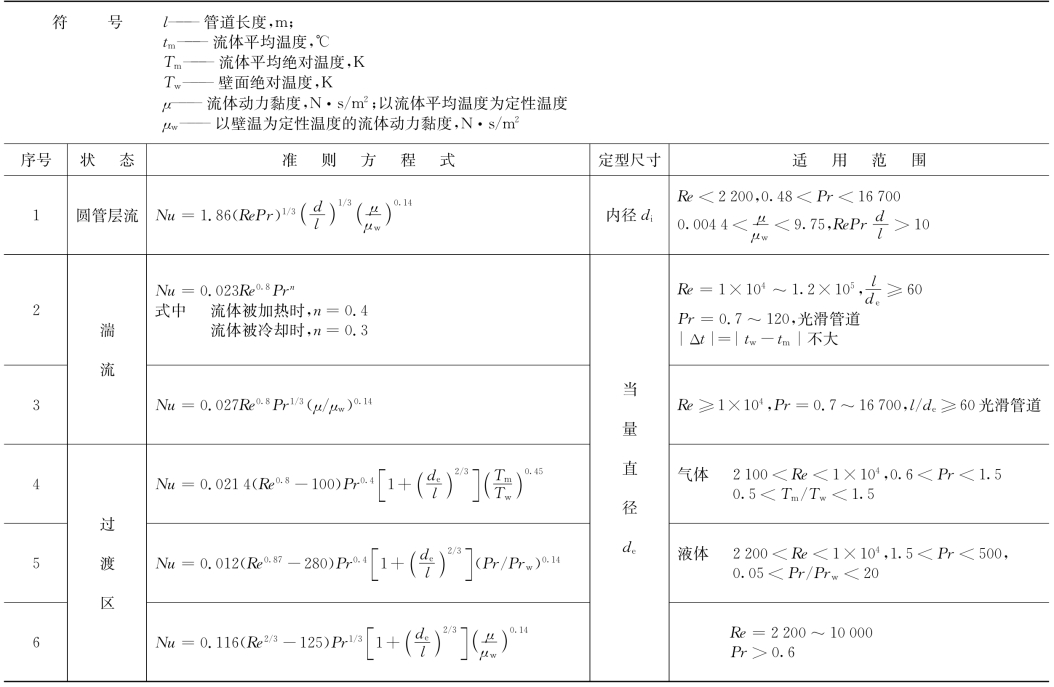
各种流动方式时的Nu或jh（或jH）与Re的关系式在传热学的相关书籍中有专门的叙述，表2.7中摘录了一些管内换热时的准则式，图2.27示出管内换热时科恩传热因子与雷诺数的关系，对于Pr＞0.7，l/d≥24的管内层流、过渡流与湍流时的强制对流换热，均可从此图查取jh值后，算出换热系数。

对于壳侧换热的计算，特别是在壳侧装有折流板时，由于其中的流动并非典型的错流，而且由于旁流和泄漏的存在，使流动的复杂性大为增加，因而历来有不少学者对壳侧换热进行多方面的研究，取得了不同的成果，以下介绍一些主要的计算方法。

（1）无折流板 一般按纵向流过管束考虑，求得当量直径后再按管内流动公式计算。

（2）盘环折流板，Re=3～2×104时

式中 Gm——平均质量速度，kg/（m2·s），计算Gm所用的基准面为由式（2.19）所示的As。

（3）弓形折流板

弓形折流板是应用最为普遍、占主导地位的一种折流板，因而对其研究较早、较多。

对于管壳式热交换器，柯尔本早在1933年就首先提出以理想管束^[1]1数据为基础的关联式，对于具有折流板的实际热交换器，其情况远比理想管束复杂，因而他的公式在使用中有很大误差。1949年，多诺霍（Donohue）发表了一个在柯尔本关联式基础上加以改进的计算方法。1950年，科恩又对多诺霍法作了一些改进，在其著作[6]中提出他的计算公式，该式的优点是同时考虑了传热问题以及壳程-管程流动、温度分布、结垢及结构等问题，是一个比较完整的设计公式。科恩提出，当缺口高度为25%，Re=2000～106时：

表2.7 管内对流换热准则方程[4]

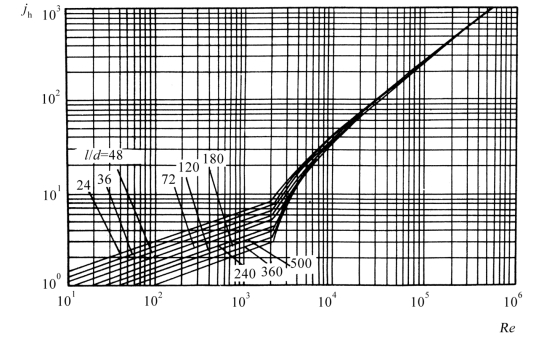
图2.27 管内换热时jh与Re的关系[5]

科恩法过去深受设计人员欢迎，但因过于简化，它的计算结果虽然换热系数还比较接近实际情况，但压降相差较远。

廷克（Tinker）在1947年提出一个引人注目的壳侧流体流动模型，它将壳侧流体分为错流、漏流及旁流等几种流路，每个流路各有自己的特点，如图2.28所示，其中：

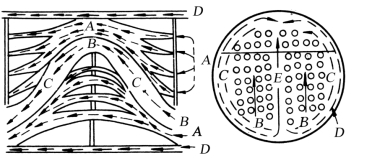
图2.28 通过壳程的各股流路

流路A：由于管子与折流板上的管孔间存在间隙，而折流板前后又存在压差所造成的泄漏，它随着管外壁的结垢而减小。此流路在环形间隙内有非常高的换热系数，但却降低了主流速度，故对传热不利。

流路B：这是真正横向流过管束的流路，它是对传热和阻力影响最大的一项。

流路C：管束最外层管子与壳体间存在间隙而产生的旁路。此旁路流量可达相当大的数值。设置旁路挡板，可改善此流路对传热的不利影响。

流路D：由于折流板和壳体内壁间存在一定间隙所形成的漏流，它不但对传热不利，而且会使温度发生相当大的畸变，特别在层流流动时，此流路可达相当大的数值。

流路E：对于多管程，因为安置分程隔板而使壳程形成了不为管子所占据的通道，若用来形成多管程的隔板设置在主横向流的方向上，它将会造成一股（或多股）旁路。此时若在旁通走廊中设置一定量的挡管，可以得到一定的改善。

廷克本人在1958年提出一种计算方法，但由于不易理解且比较繁琐，故而未获普遍使用，但他的流动模型却成为日后其他一些先进计算方法的物理基础。

1960年，由贝尔（Bell）执笔写出了美国特拉华（Delaware）大学经过多年研究所得的壳程计算科研实验报告，又于1963年提出最终报告。其后贝尔又将此法加以改进，该法的特点是利用大量实验数据，引入各流路的修正系数，可以说是目前公开发表的各种方法中最先进的一种，以下介绍贝尔法的主要内容。

贝尔法的中心内容是首先假定全部壳程流体都以错流形式通过理想管束，求得理想管束的传热因子，然后根据热交换器结构参数及操作条件的不同，引入各项校正因子[8][9]。

在介绍贝尔法以前，除了了解2.2.3节所述的结构参数外，还须解决其他一些结构参数的计算。

（1）总管数nt从图纸上读出。

（2）错流区管排数Nc最好从图纸上读出，否则按下式估算：

sp——见图2.26

（3）错流区内管子数占总管数的百分数Fc见式（2.15）。

（4）每一缺口内的有效错流管排数Ncw

（5）错流面积中旁流面积所占分数Fbp

若有E流路存在时，则

式中 NE——管程隔板所占的通道数（E流路数）；

lE——E流道的宽度。

（6）一块折流板上管子和管孔之间的泄漏面积Atb

式中 δtb=dH-do，dH为管孔直径。

（7）折流板外缘与壳体内壁之间的泄漏面积Asb

式中 Db——折流板直径。

（8）流体通过缺口的流通面积Ab见式（2.13）及（2.14），Ab为该两式相减后的值。

（9）缺口的当量直径Dw（用于Re≤100的情况），这个值仅仅在计算层流区内（Re≤100）的压降时才需要。

（10）折流板数目

若进、出口段板间距不等于ls，则

式中 ls，i，ls，o——分别为进、出口段从折流板到管板的距离。

在明确结构参数后，贝尔法计算壳程换热系数的过程如下：

（1）由图2.29查出在热交换器中心线处，假定壳程流体全部错流流过管束，在此理想管束中纯错流时的柯尔本传热因子jH

(www.xing528.com)

式中 Gs——壳程流体质量流速，kg/（m2·s）；

μ——以流体平均温度为定性温度的黏度，Pa·s；

μw——以壁温为定性温度的黏度，Pa·s；

cp——流体比热，J/（kg·℃）。

（2）由图2.30查取折流板缺口的校正因子jc，jc是Fc的函数，对于缺口处不排管的结构，jc=1。

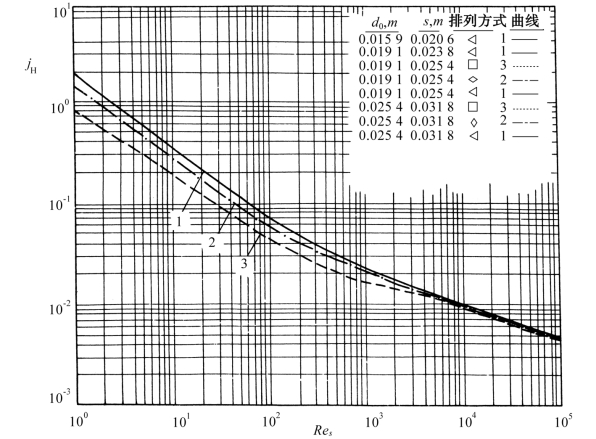
图2.29 理想管束的传热因子[11]

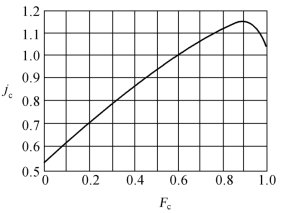
图2.30 折流板缺口校正因子jc[9]

（3）由图2.31查取折流板泄漏影响的校正因子jl（A和D流路），它是Asb/（Asb+Atb）及（Asb+Atb）/Ac的函数。

（4）由图2.32查取管束旁通影响的校正因子jb，它是Fbp和Nss/Nc（Nss为每一错流区内旁路挡板对数，Nc为错流区内管排数）的函数。

（5）由下式计算当热交换器进、出口段折流板间距不等时的校正因子js

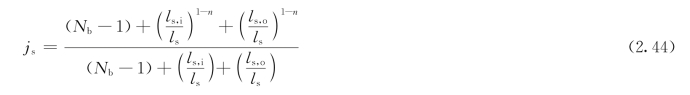
式中，当Re≥100时，n=0.6；

当Re＜100时，n=1/3。

（6）当雷诺数较低时（壳程Re＜100），将出现逆向温度梯度，采用校正因子jr以考虑其影响。

当Re≤20时，从图2.33中查取。

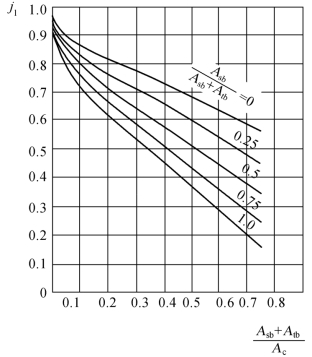
图2.31 折流板泄漏校正因子jl[9]

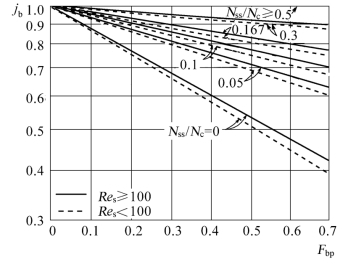
图2.32 旁通校正因子jb[8]

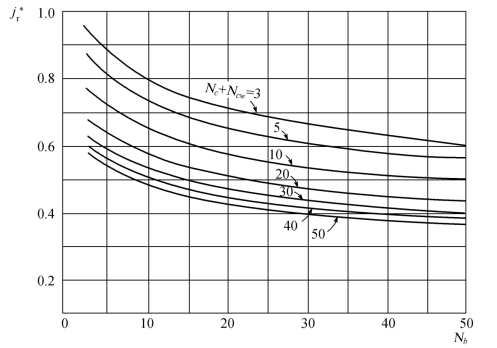
图2.33 低Re时逆温度梯度的校正因子[8]

当20＜Re＜100时，先从图2.33中查得，再从图2.34中查取jr。

（7）计算壳程传热因子jo

并按式（2.43）算出壳程换热系数αo。

2）与换热系数有关的几个问题

（1）定性温度

准则数中的物性都随流体温度的变化而变化，因而所有准则方程式中都指明了以哪个温度为准的物性参数，用此温度确定物性，即定性温度。

图2.34 中等Re时逆温度梯度的校正因子jr[8]

定性温度的取法大致有：（a）取流体的平均温度为定性温度；（b）取壁面温度为定性温度；（c）取流体和壁面的平均温度为定性温度。在查阅各类参考书籍时，必须弄清它的定性温度表示方法。

对于油类及其他高黏度流体，由于加热或冷却过程中黏度要发生很大变化，这时若用流体进、出口的算术平均温度作为定性温度，往往会使换热系数的数值有很大误差，虽然这时可以分段计算，但其工作量很大。因而目前工业上常采用卡路里温度（CaloricTemperature）来计算管内、外流体的换热系数，在此温度下计算得到的传热系数就被视为常量，它和对数平均温差的乘积等于变化的传热系数和实际温差的乘积。

参考文献[6]对卡路里温度作了介绍，其计算公式如下：

热流体的平均温度

冷流体的平均温度

式中的Fc称为卡路里分数，落合安太郎^[2]1建议可取值如下：

壳侧流体被管侧的水冷却时，Fc=0.3；

壳侧流体被管程的水蒸气加热时，Fc=0.55；

壳侧和管侧均为油时，Fc=0.45；

黏度在10-3Pa·s以下的低黏性液体，Fc=0.5。

（2）定型尺寸

努塞尔准数、雷诺准数等的定义式中，l为定型尺寸。通常是选取对流体运动或传热发生主导影响的尺寸作为定型尺寸。例如，在圆管内的换热过程取管子内径di，在管外强迫流动换热时取管子外径do，而对非圆形管道则取其当量直径de。在一般情况下，当量直径的定义为

式中 A——流体的流通截面积；

U——湿周边或热周边长，在计算阻力时，它是全部润湿周边；在传热计算时，是参与传热的周边。

各种流通截面的当量直径计算公式可查本书的附录B。

也有的文献在计算阻力及传热时全用润湿周边来计算当量直径，因此在应用准则方程式时，还应注意当量直径的取法是否有特别的说明。

（3）黏度修正

在某些准则方程式中，为了考虑非定温流动和热流方向对换热的影响，常乘有（μf/μw）n，（Prf/Prw）m因子的修正项，或者在准则方程式中的Pr项对加热和冷却采用不同的方次。此修正项的计算，往往由于壁温未知而要用试差法；但也可取近似值：液体被加热时，取（μ/μw）0.14≈1.05，液体被冷却时，则取（μ/μw）0.14≈0.95。对气体，若也用（μ/μw）0.14因子来校正，则不论加热或冷却，均可取（μ/μw）0.14=1.0。

（4）同时存在对流换热与辐射换热的处理

如果流体是具有辐射能力的气体（例如烟气）且温度较高时，则需要考虑流体与壁面之间的辐射换热，可将其并入对流换热，用总换热系数来处理。这时，把总换热系数写成

其传热量的计算公式仍为

Q=αFΔt

式中 αc——对流换热系数；

αr——辐射换热系数，

α——总换热系数；

Co——黑体辐射常数，其值为5.67W/（m2·K4）；

εn——换热系统的组合黑度；

φ——角系数；

T1、T2——两辐射物体的绝对温度。