传热有效度在其他流动方式下的影响

Kays和London对于许多流动方式的ε-NTU关系作了介绍[5]，并绘成线图，供设计时引用。下面仍以〈1-2〉型和错流式热交换器为例进行推导。

1）〈1-2〉型热交换器

该型热交换器的传热有效度可直接按式（1.18）作进一步分析求得。即

注意到S为每一流程单位长度上的传热面积，故

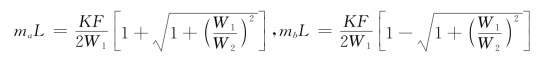
为了推导的方便，假定热流体是小热容量流体，故

将其代入式（1.18），得

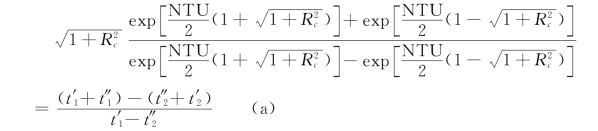
令，则式（a）等号之左等于

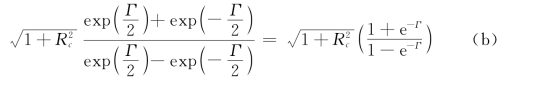
式（a）等号之右，由于

故

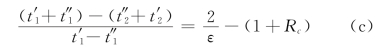
于是式（a）得到了简化，成为

最后得到

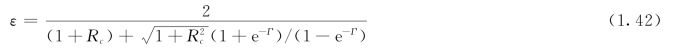
由此绘成的线图，见图1.20。管侧流体相对于壳侧流体来说，无论是先逆后顺，还是先顺后逆，式（1.42）和图1.20均适用。对于〈1-2n〉型热交换器，其ε与〈1-2〉型相差很小，因而也可用上述结论。

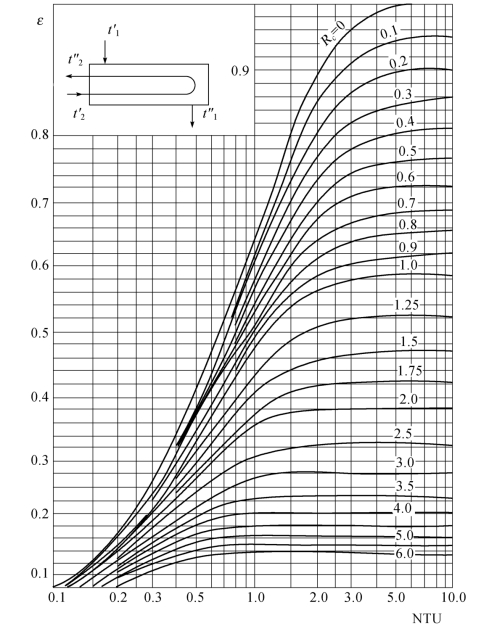
图1.20 〈1-2〉型热交换器的ε[4]

2）两流体中仅一种有混合的错流式热交换器

这种流动方式已表示在图1.4（b）中，在推导平均温差时已得到过下式：

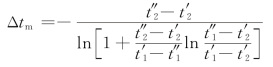
考虑到

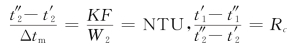
而由式（1.15）

于是上式成为

或

(www.xing528.com)

此即ε与NTU间的关系，依此绘成的线图，见图1.21。

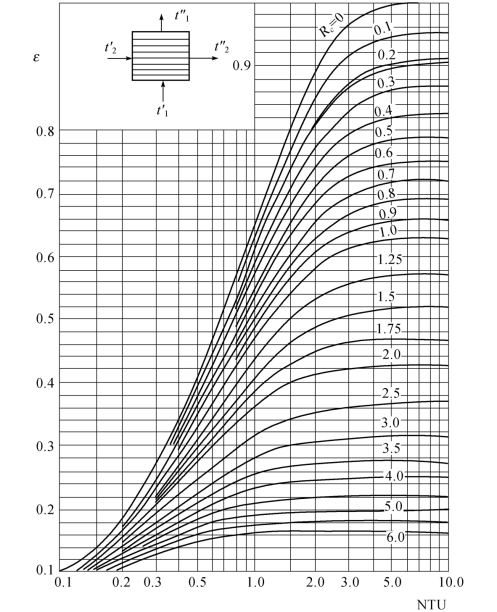
图1.21 两种流体中仅有一种混合的错流式热交换器的ε[4]

3）其他更为复杂的流型

举出如下一些计算公式。对于〈2-4〉型，有

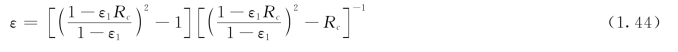
式中ε1为由式（1.42）算得的值，它对〈2-4n〉型也适用。按式（1.44）所作的线图，见图1.22。

对于两种流体都不混合的错流式热交换器，其近似关系如下，但下式只有在Rc≈1时才有把握，一般情况下，推荐使用图1.23而不使用下式[6]。

对于多次错流，其组合方式很多，图1.24所示为流体A在管程内互不混合，流体B混合，但两种流体在两段间均有混合的二次错流，其传热有效度

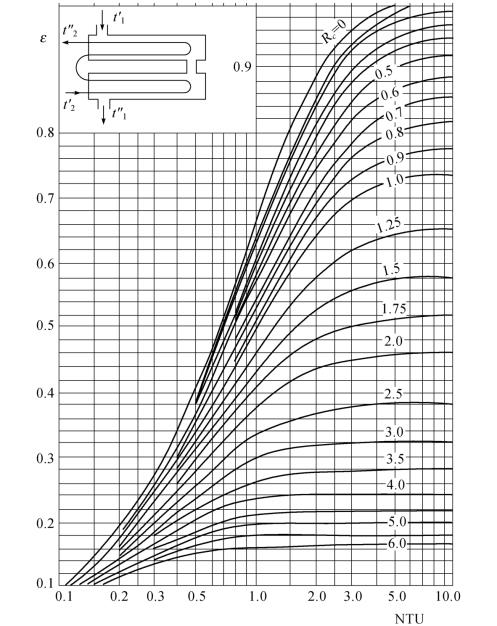
图1.22 〈2-4〉型热交换器的ε[4]

其中εi为各分段的传热有效度。当各段传热系数及传热面积相等时，总传热单元数的1/2即为分段的传热单元数，于是可利用式（1.43）或图1.21得出εi。

图1.25表示的是三次错流，A为非混合流，B为混合流，但A、B在三段之间均有混合，其传热有效度[2]：

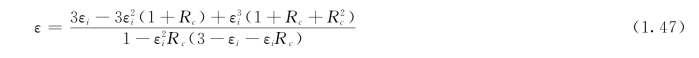
其中的εi仍为各分段的传热有效度，它是以总传热单元数的1/3作为分段的传热单元数，利用式（1.43）求得的。

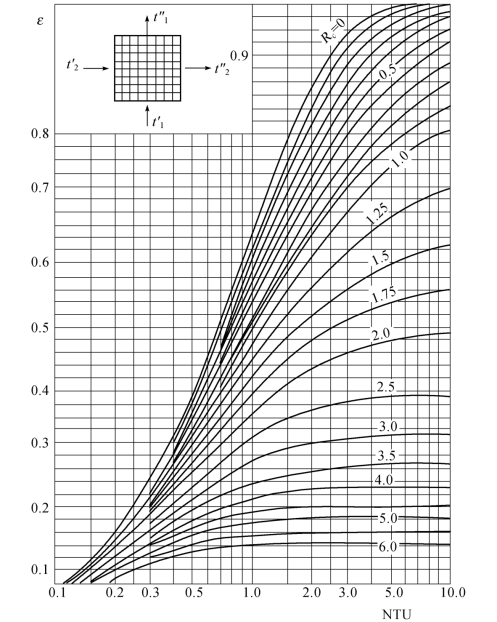
图1.23 两种流体都不混合的错流式热交换器的ε[4]

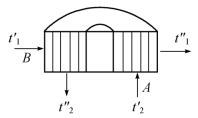
图1.24 二次错流

图1.25 三次错流

[例1.4] 有一管式空气预热器，烟气流过管内，在管程间有横向混合，如图1.26所示，已知其传热面积F=1353m2，传热系数K=14 W/（m2·℃），烟气的热容量W1=14460W/℃，进口温度t′1=465℃，空气热容量W2=10540W/℃，进口温度t′2=135℃，求烟气及空气的出口温度。

[解] 传热单元数，热容量比=0.729，分传热单元数。

查与本题相应的一次错流的线图1.21，得εi=0.485，于是可利用式（1.46）计算总的传热有效度

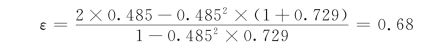
空气出口温度

由热平衡可求出烟气出口温度

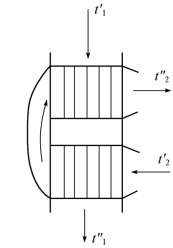
图1.26 例1.4附图