顺逆流传热效率的比较研究

由前已知，顺流时

或

由热平衡关系，应有

将式（b）代入式（a）中

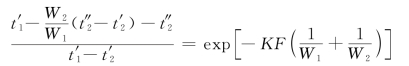
或

若冷流体是热容量小的流体，则利用式（1.33c）的关系，式（c）变成

若热流体是热容量小的流体，则式（a）变成

由式（d）和式（e），可以将顺流时的传热有效度统一写成

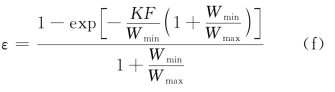
现将其中的定义为传热单元数，且以NTU表示，即

它代表了热交换器传热能力的大小，也是一个无因次数。若再令

则顺流时的ε-NTU关系式为

这样就把热交换器的传热有效度表示成ε=φ（NTU，Rc）的形式。用式（1.36）所表达的顺流时的ε、NTU、Rc三者的关系做成的线图，见图1.18。

当任一种流体是在相变条件下传热，即Wmax趋于无穷大时，Rc=0，式（1.36）简化成

而当两种流体的热容量相等，即Rc=1时，

逆流时，可以用类似的推导方法得到ε、NTU、Rc三者的关系

图1.18 顺流热交换器的ε[4]

图1.19即为依式（1.39）做成的线图。从式1.39可见，当一种流体有相变，即当Rc=0时，逆流的ε与NTU之关系与式（1.36）相同，而当两种流体的热容量相等，即当Rc=1时，经推导式（1.39）成为

由以上分析可见，它们都是在传热方程式和热平衡方程式的基础上推导得到的，这与推导平均温差的过程完全相同。只不过在平均温差法中是整理成ψ=f（P，R）的关系，而在ε-NTU法中是整理成ε=φ（NTU，Rc）的关系，因而两者并无本质区别，只是处理方法不同。

在应用ε-NTU法时，应注意以下几点：

（1）在同样的传热单元数时，逆流热交换器的传热有效度总是大于顺流的，且随传热单元数的增加而增加。在顺流热交换器中则与此相反，其传热有效度一般随传热单元数的增加而趋于定值。因此在设计顺流热交换器时，当传热有效度达到一定值后，没有必要再增加传热单元数。

图1.19 逆流热交换器的ε[4]

（2）按照平均温差法和ε-NTU法所作的定义比较，当W2=Wmin时，存在如下关系：(www.xing528.com)

ε=P; Rc=R

而且

或

当W1=Wmin时的关系为

ε=P′;Rc=R′

而且仍有式（1.41）所示的关系，并且

因而就可借此将某种流动方式的NTU=φ（ε，Rc）关系转化成ψ=f（P，R）或ψ=f（P′，R′）的关系。

（3）考察一下传热有效度ε的公式（1.33b）和式（1.33c），它们实际上是以温度形式反映出热、冷流体可用热量被利用的程度，故此两式实质上表示了热流体的温度效率和冷流体的温度效率，因此除通常使用的传热有效度-传热单元数外，还有一种温度效率-传热单元数法[4]，后者可任意对热流体或冷流体进行定义，而不必区分何者为小热容量流体，给计算带来许多方便。

于是，仍用符号ε表示温度效率时：

热流体的温度效率，冷流体的温度效率。与之相应的

Rc1=W1/W2,Rc2=W2/W1

NTU1=KF/W1,NTU2=KF/W2

这时，ε=φ（NTU，Rc）的关系不变，但Rc值可能小于、等于或大于1，因此本书的ε-NTU图中，同时绘有Rc≤1和Rc＞1的曲线，而当Rc≤1时，温度效率恰恰就是传热有效度。

以上各点，对于后面所述其他流型的ε-NTU关系同样适用。

[例1.3] 温度为99℃的热水进入一个逆流热交换器，将4℃的冷水加热到32℃。热水流量为9360kg/h，冷水流量为4680kg/h，传热系数为830W/（m2·℃），试计算该热交换器的传热面积和传热有效度。

[解] 按题意可将温度工况示意如下：

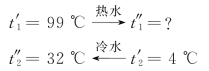
热水热容量

冷水热容量

因而

W1=Wmax,W2=Wmin

由热平衡关系，故

而

将以上数据代入式（1.39），即，得

NTU=0.38

故传热面积

此例若以平均温差法计算时

所需传热面积仍为

F=5441.8×28/(830×73.8)=2.49m2

若用热流体的温度效率计算ε、Rc、NTU三值时，可得到ε1=0.147，Rc1=2，NTU1=0.19，而F仍为2.49m2。