流体比热或传热系数变化时的平均温差调节策略

如前所述，平均温差的各个公式及线算图都是在假定流体物性（包括比热）恒定的基础上推导得到的。事实上这种情形几乎没有。由于

dQ=mcdt

因而当比热为定值时，流体温度的变化与吸收（或放出）的热量成正比，两者表现为线性关系，如图1.15所示的冷流体那样。实际上，流体的比热总是随着温度的改变有或多或少的变化，因而温度与传热量之间就不会是线性关系，如图1.15所示的热流体那样。

如果在讨论的温度范围内，比热随温度有显著变化（大于2～3倍），应当采用积分平均温差来计算。这种算法的出发点是：虽然流体的比热在整个温度变化范围内是个变量，但是若把温度变化范围分成若干小段，每个小段内的温度变化小，就可将流体的比热当做常数来处理。因此在每一小段中的传热温差就可采用对数平均或算术平均的方法计算。具体步骤如下：

（1）在已知流体比热随温度而变化的关系时，可按

作出如图1.15所示的那种Q-t图。或当备有流体的温-熵图或焓-熵图时，作出I-t图。图的纵坐标Q（或I）从上而下表示冷流体从它的进口起所吸收的热量，从下而上表示热流体从进口起所放出的热量；横坐标则表示流体的温度。

图1.15 Q-t图

（2）将Q-t曲线分段，每段近似取为直线关系，并求出相应于各段的传热量ΔQi。

（3）按具体情况用对数平均的方法或算术平均的方法求出各段的平均温差Δti。

（4）计算积分平均温差：

因为各段的传热面ΔFi=ΔQi/KiΔti，所以总传热面

又

使式（a）和（b）相等，并假定各段的传热系数相同，则可得到总的平均温差，即积分平均温差，有时也用一个特定的符号（Δtm）int表示：

以上步骤也可按每段传热量相同的方法分段，设这时有n段，则每段的传热量于是式（a）成为

从式（b）、（c）两式可得积分平均温差

如图1.1（f）和图1.1（g）所示的热交换过程，一种流体处于冷却并冷凝、过冷，或加热并沸腾、过热时，相当于比热发生剧烈变化的情况，也应考虑分段计算；又如图1.1（h）所示的热交换情况，其中热流体含有不凝结气体，这时所放出的热量不与温度的变化成正比，也应分段计算平均温差。

在推导对数平均温差时也曾作过传热系数不变的假定，实际上它在整个传热过程中也是变化的，不过在工程的热交换器中由于物性的变化一般不大，反映到传热系数的变化上就更小，因此，一般工程计算中可以把热交换器中各部分的传热系数视为常量。若传热系数变化确实较大，仍可采用分段计算的办法，把每段的传热系数作为常数，分段计算平均温差和传热量，即取

式中 ΔQi——某段传热量；

Ki——该段的传热系数；

Δti——该段的平均温差；

Fi——该段的传热面积。

而总传热量为

如果K随温差Δt成线性变化，或K随两流体中任一种流体温度成线性变化时，对于顺流或逆流都可用下式计算

式中 K′、Δt′——Fx=0处的传热系数和两流体温差；

K″、Δt″——Fz=F处的传热系数和两流体温差。

对于其他流型，作为一种近似的计算方法，可在上式等号之右以温差修正系数ψ乘之，而Δt′、Δt″为按逆流情况计算的端部温差。

[例1.1] 有一蒸汽加热空气的热交换器，它将质量流量为21600kg/h的空气从10℃加热到50℃。空气与蒸汽逆流，其比热为1.02kJ/（kg℃），加热蒸汽系压力p=0.2MPa、温度为140℃的过热蒸汽，在热交换器中被冷却为该压力下的饱和水。试求其平均温差。

[解] 由水蒸气的热力性质表查得蒸汽有关状态参数为：

饱和温度ts=120.23℃；饱和蒸汽焓i″=2707kJ/kg

过热蒸汽焓i=2749kJ/kg；汽化潜热r=2202kJ/kg于是可算出整个热交换器的传热量：

图1.16 例题附图

从热平衡关系求蒸汽耗量M1：

∵ Q=M1[(i-i″)+r]

∴

因为在热交换器中存在冷却和冷凝段，因而将之分两段计算，如图1.16所示。

在过热蒸汽的冷却段放出的热量

在冷凝段，则为(www.xing528.com)

Q2=M1r=0.1091×2202=240.24kJ/s

为了分段求平均温度，应先求出两分段分界处的空气温度ta。

∵

∴

由此，冷却段之平均温差

而冷凝段之平均温差

总的平均温差为

从此例可见，以过热蒸汽作为加热流体时，只要过热度不是很大的场合，过热蒸汽的冷却段在整个热交换器中所起的作用不是很大，因而即使以冷凝段的参数来计算，其误差也很小。

[例1.2] 某空分装置中以产品氧气冷却空气，已知空气流量V1=110Nm3/h（这里N是指标准状态），氧气流量V2=150Nm3/h，压力p1=2000kPa，p2=140kPa，空气与氧气逆流流动，其进、出口参数为

空气

氧气

因为该热交换器在低于周围环境的温度下工作，根据经验，其冷损QL=280kJ/h。试求该热交换器的平均温差。

[解] 由已知条件，作出该热交换器内的流体流动示意图（见图1.17）。由于氧气和空气的比热在所处压力下随温度的不同有较大变化，故应用积分平均温差的求法，首先作出它的I-T图。具体过程如下：

1）任取一个断面m-n，写出该断面以下的热平衡方程式

式中

ΔI1、ΔI2——分别为该段中空气焓的变化值与氧气焓的变化值，kJ/（kgmol）；

ΔQL——该段的冷损，kJ/h。

假定冷损按氧气的焓差成比例分配，即每段的冷损：

将式（b）代入式（a），则得

即

所以

由于这一小段是任意选取的，因此它也是热交换器任意一个截面上空气焓差和氧气焓差之间的关系。

2）以空气进口端作起点，作如下计算：

（1）按氧气在热交换器内吸收的热量分段，以210kJ/kgmol为一段，共分成六段[最后一段为226kJ/（kgmol）]。从而可知各段分界处的I2（见表1.1）；

表1.1 空气与氧气的焓和温度的变化

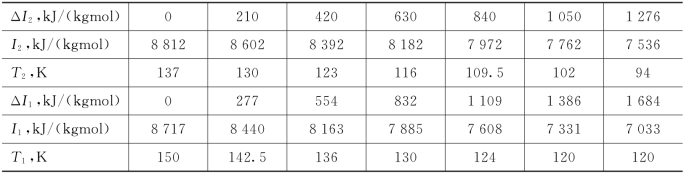
（2）根据各分段处的I2值，用氧的温-熵图，查出与此相对应的T2值；

（3）由式（c）算出该小段空气的焓差ΔI1，并算出空气的焓I1；

（4）再根据I1，用空气的温-熵图查出相应的空气温度T1。

计算的结果列在表1.1上。从表的最后一行可见，空气的最后两段已在液化区。

3）以I为纵坐标，T为横坐标，用表1.1中数据作出I-T图（图1.17）。

4）以每个小段的T2与T1的进出口值求算术平均温差，其值如下：

Δt1=12.75K Δt2=12.75K Δt3=13.5K

Δt4=14.25K Δt5=16.25K Δt6=22K

5）用式（1.28）求积分平均温差

图1.17 空气、氧气的I-T图