其他流动方式下的平均温差分析

顺流和逆流属于最简单的流动方式，工程应用上往往由于需要传递大量的热而又受到空间的限制，而要采用多流程的、错流的以及更为复杂方式流动的热交换器（见图0.1）。

在这里，还要对混合流与非混合流加以区别，以图1.4所示的错流为例，图（a）为带翅片的管束，在管外侧流过的气体被限制在翅片之间形成各自独立的通道，在垂直于流动的方向上（横向）不能自由运动，也就不可能自身进行混合，我们称该气体为非混合流。与此类似，管内的流体也被约束在互相隔开的管子中，所以它也是非混合流。而图（b）中的管子不带翅片，管外的气流可以在横向自由地、随意地运动，称为混合流，管内的流体仍属于非混合流。错流式热交换器中，两种流体的流动虽然简单，可是非混合流的温度在流动方向上和垂直于流动的方向上都是变化的。

混流和错流流动的平均温差的计算要比顺流、逆流复杂，但在附加一些简化的假设条件后，都可用数学方法导出。不过这些公式很繁，因而常将这些流动方式的流体进出口温度先按逆流算出对数平均温差，然后乘以考虑因其流动方式不同于逆流而引入的修正系数ψ，即

式中 Δtlm，c——按逆流方式由式（1.11）算得的对数平均温差；

ψ——修正系数。

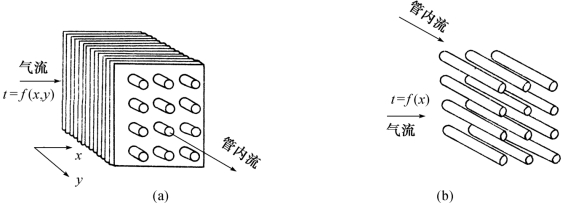
图1.4 错流热交换器

（a）两种流体都不混合 （b）一种流体混合，另一种流体不混合

为了求取ψ值，可对式（1.10）进行一些变换，将它写成逆流的方式，即

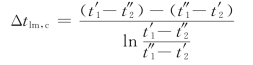
若令

作为辅助参数，则可将Δtlm，c表达成P、R及的函数，即

由P、R的定义可知，P的数值代表了冷流体的实际吸热量与最大可能的吸热量的比率，称为温度效率，该值恒小于1。R是冷流体的热容量与热流体的热容量之比，可以大于1、等于1或小于1。

对于某种特定的流动型式，ψ是辅助参数P、R的函数，即

ψ=f(P、R)

此函数形式因流动方式而异，由于篇幅所限，下面只举出两个推导该函数的例子。

1）热流体在管外流动为一个流程，冷流体在管内先逆流后顺流流动两个流程的〈1-2〉型热交换器

在对该种方式进行推导时，除了推导对数平均温差时所用的假定外，还假定：①管外流体在横向有充分的混合；②管内两流程面积相等。图1.5为此种流动方式流体温度变化的示意图。对整个热交换器来说，其热平衡方程式为

对x=x到x=L段的热平衡，有

在微元段dx内，设热流体放出热量为dQ1，而冷流体在第一流程吸收热量为，在第二流程吸收热量为，则

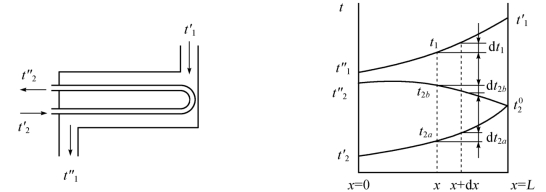
图1.5 先逆后顺的〈1-2〉型热交换器及其温度变化示意图

故

若以S表示每一流程中单位长度上的传热面积，则

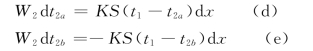
将式（d）、（e）代入式（c）得

将此式对x微分，则

用式（d）、（e）代入式（g），就成为

再将式（b）代入式（h）并经整理之后可得

此为壳侧流体温度沿着流动方向变化的微分方程式。为了求解此式，引入新变量

其中，为热流体的起始温度，作为常量看待。于是式（i）变成

这是一个二阶齐次线性常微分方程式，设其解为

代入式（k）中，则为

解此一元二次方程，可得到m的两个解：

式中

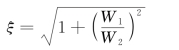
因此，由式（l）可得式（k）的通解为

其中的待定常数Ma、Mb可由边界条件

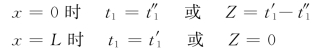
确定。将其代入式（n）中，可求出待定常数

将式（p）代入式（n），则

式（q）表示了壳侧流体温度沿距离x的变化规律。

若将式（n）对x求导，可得壳侧流体温度的变化率，即

将式（f）代入式（r），考虑到边界条件

则

将由式（1.17）及式（p）确定的ma、mb及Ma、Mb代入式（s）就有

进行整理后得

分子和分母同除以exp（mbL），整理之后就可得到

根据式（1.17），有

另一方面，对热交换器的整体，可以把传热方程和热平衡方程结合写成

其中2SL=F为传热面积，所以(www.xing528.com)

由式（u）、（v），得

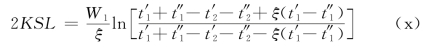
将式（x）代入式（w），并考虑到

进行整理之后，得到计算平均温差的公式如下：

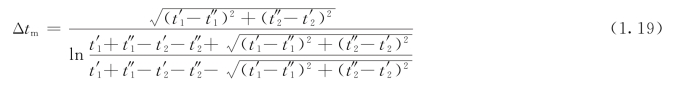
利用式（1.14）、（1.15）给出的辅助函数P、R，可将该式改写成

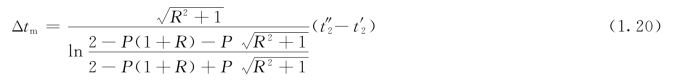
由式（1.13）及式（1.16），又有

使式（1.20）及式（1.21）相等，经过一些整理之后可得

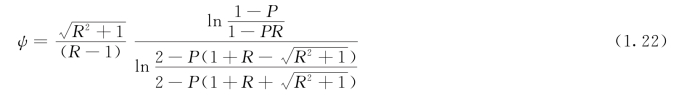
由上可见，该流动方式的平均温差可直接用式（1.19）、（1.20）计算，或用式（1.13）计算，其中的ψ值则用式（1.22）算出。

对于先顺流后逆流的〈1-2〉型热交换器推导的结果表明，式（1.22）也是适用的。

分析还表明，即使对于壳侧为一个流程、管侧为偶数流程的〈1-4〉型、〈1-6〉型、……、〈1-2n〉型热交换器，式（1.22）仍可近似使用，因为它们的ψ值差得很小。

2）两种流体中只有一种流体有横向混合的错流式热交换器

图1.6为这种流动方式以及流体温度变化的示意图。

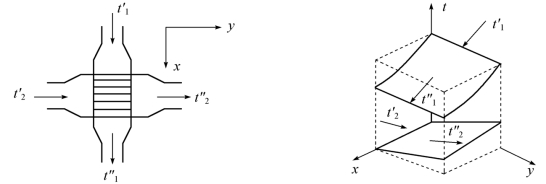
图1.6 只有一种流体发生横向混合的错流式热交换器及其温度变化的示意图

设有长为L、宽为B的壁面，热流体流动方向为x，在y方向发生混合，冷流体流动方向为y，横向不混合，如图1.7所示。

因而

t1=f(x),t2=f(x,y)

两种流体各自在入口处具有均匀的温度，分别为和，另外补充假定冷流体在横向不发生导热。

由微元面积dF（=dxdy）的传热方程式和热平衡方程式，有

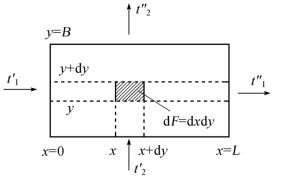
图1.7 只有一种流体作横向混合的情况

或

因为t1与y无关，可将式（a）写成

将式（b）在y=0至y=B，t2=t′2至t2=t2（x，B）区间分别积分，得

该式表示了在某一位置x处，冷流体出口温度t2（x，B）与x处热流体温度t1之间的关系。

另外，对于长为B、宽为dx的狭条面积上两流体间的热平衡关系为

将式（c）代入此式并经整理后可得

对式（e）分别从x=0至x=L以及至进行积分，得

由于对整个热交换器存在着如下的热平衡方程和传热方程

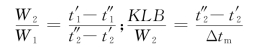
因而式（f）成为

考虑到式（1.16）以及

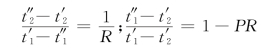
则由式（1.23）可得

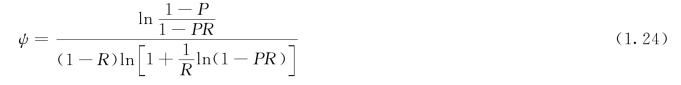
若冷流体发生横向混合而热流体不混合时，仍可利用式（1.24）进行计算，但辅助参数应取为

综合上述，对于只有一种流体有横向混合的错流式热交换器，可将辅助参数的取法归纳为

工程上为使计算方便，通常将求取ψ值的公式绘成线图，根据P、R值，即可查出ψ值的大小，如图1.8～图1.14所示。

ψ值总是小于或等于1的，从ψ值的大小可看出某种流动方式在给定工况下接近逆流的程度。在设计中除非出于降低壁温的目的，否则最好使ψ＞0.9，若ψ＜0.75就认为不合理，此时可采用多壳程（例如将〈1-2〉型改为〈2-4〉型）或多台串联的方式来代替，因为这样可使ψ值提高，使流动方式更接近于逆流。

从ψ值的推导过程可见，它是在分析热交换器微元面积的热平衡方程和传热方程的基础上而获得的，即

如果把热交换器中的两种流体交换一下，即下标1改为冷流体，下标2改为热流体，此时上式并不因此改变，故ψ值也不改变。但是根据前面对P、R两值所作的定义，将改变了下标之后的P、R以P′、R′表示时，应有

因而下标改变后相当于用代替P和R。亦即

根据这一点，在查取ψ值的线图时，当R超过线图所示范围或当某些区域的ψ值不易读准时，可用P′和R′查图，对ψ值的大小并无影响。

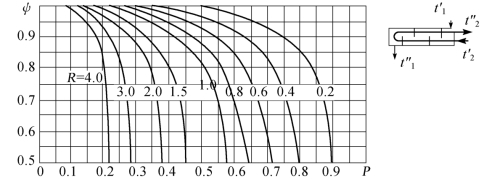
图1.8 〈1-2〉型热交换器的ψ值[1]

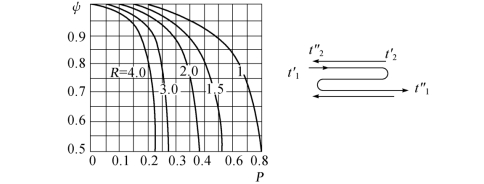
图1.9 一个流程顺流，两个流程逆流的热交换器的ψ值[3]

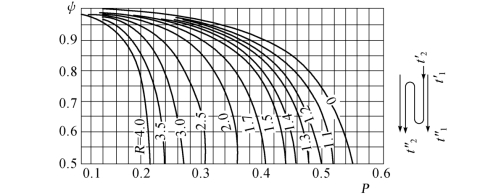
图1.10 一个流程逆流，两个流程顺流的热交换器的ψ值[3]

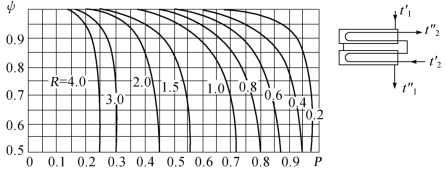
图1.11 〈2-4〉型热交换器的ψ值[2]

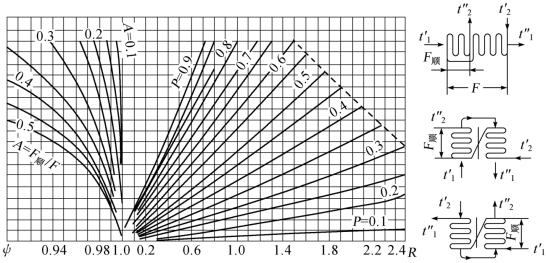
图1.12 串联混合流型热交换器的ψ值[3]

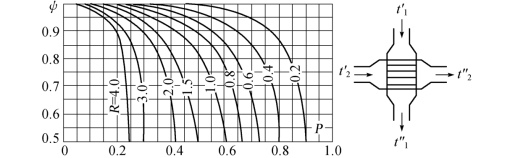
图1.13 只有一种流体有横向混合的一次错流热交换器的ψ值[3]

图1.14 两种流体均无横向混合的一次错流热交换器的ψ值[3]