完善概率图模型的技巧与方法

在15.4小节中，我们详细讨论了一组具有链式结构的概率图模型：隐Markov模型，参见图15.7。进一步，我们给出了关于隐藏节点的最大后验估计分析，以及如何通过动态规划算法，（根据新引进的可见节点）来更新最大后验估计结果。对于实际应用，我们还留有一个待解决的问题：如何获取或估计转移矩阵P、似然关系Q中的参数？一般情况下，似然关系Q被设置为Gauss分布，方差σ2仍然是待确定的参数。图15.8中的结果也说明：选取不同的方差σ2进行最大后验估计，结果之间存在一定差别。我们首先探索隐Markov模型的参数估计问题，即如何确定P和Q，然后将其推广到更一般的情况：具有链式结构的概率图模型。

16.1.1　隐Markov模型的参数估计

对于隐Markov模型，当新的可见节点Wn被引入后，我们通过

去选定(15.73)中的xm，然后根据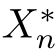，从众多的“最优估计结果”序列中，选取出以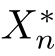结尾的序列：

作为新的最大后验估计结果，参见15.4小节内容。式(16.2)中的最大后验估计结果依赖于参数P和Q的选取，于是，我们找到了一种优化估计参数P和Q的依据：使得式(16.2)中的最大后验估计结果的“效果最好”。要做到这一点，我们首先需要找到一种方式，对的效果进行“评价”。

在最大后验估计过程中，一组可见节点W 0,W 1,W 2,···,Wn也被同时获取到了，因此，我们可以尝试通过：分析与W 0,W 1,W 2,···,Wn之间的“耦合度”，来评价式(16.2)中的最大后验估计结果的“效果好坏”。相应的，似然条件概率

正好给出了两组数据之间“耦合度”的一种描述方式。经过上述分析，我们明确了参数估计的具体数学描述：通过选择P和Q中的参数来最大化似然条件概率(16.3)。虽然我们还没有得出具体算法，但是，至少已经把模型建立起来了。最坏的情况无非是用“蛮力法”去试验各个参数，然后进行选择。当然，我们应该继续探索具体求解算法。根据式(15.70)，似然函数(16.3)的具体形式为：

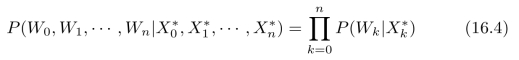
假设P(Wk|Xk)服从Gauss分布，我们可以对(16.4)取对数，再进行优化求解，也就是说，

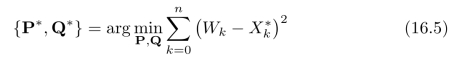
注意，通过参数{P,Q}确定是一个“隐式过程”，无法进行求导，参见式(15.79)和(15.75)。因此，不能直接用“偏导数等于零”的极值条件来进行求解。

在给出具体算法之前，让我们先来把这个问题具体分析一下。首先，我们可以求出与可见节点W 0,W 1,W 2,···,Wn耦合度最高的一组隐藏节点，记为：

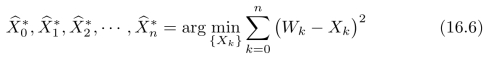
每一个隐藏节点的求解也非常简单和直接，

也就是说，逐个查找与每一个可见节点最接近的隐藏节点。我们是否能让根据式(16.5)求出来的估计结果等于式(16.6)的最优解？答案是不能！因为最大后验估计结果是根据参数{P,Q}优化计算出来的，因此，在序列中，只有部分节点能够与序列匹配上。当我们调整参数{P,Q}后，根据15.4小节中介绍的动态规划算法，会得到一组新的最大后验估计结果。同样地，在新得到的序列中，也只有部分节点能够与序列匹配上。具体地说，我们可以通过调整参数{P,Q}使得某一个节点匹配上后，但是，某些原来匹配上的节点可能会因此而变得匹配不上。

这并不代表前面的分析是毫无意义的，我们的探索不一定成功，但是，我们不能因此而停止探索。相对于知识本身而言，有时候更有价值的是前人探索知识过程中所积累的经验。我们写这本书的目的也是更多地想将这些经验介绍给大家。事实上，后面我们会谈到：通过评估某个节点X k的状态变化对整个“最优估计结果”序列的影响，我们可以基于上述理论分析得出相应的参数估计算法。在介绍这个算法之前，我们需要补充一些理论分析，建立起关于隐Markov链的条件概率模型。

16.1.2　条件概率模型

在前面的分析中，我们尝试采用15.4小节中介绍的动态规划算法，即习题15.3中详细探讨的V iterb i算法，来直接得出最大后验估计结果，然后，通过最大化可见节点序列W 0,W 1,W 2,···,Wn与最大后验估计结果之间的“耦合度”，来估计参数P和Q。遗憾的是，我们在求解最大“耦合度”的过程中遇到了困难，只能通过“蛮力法”来进行计算求解。因此，我们不得不“从头开始”建立理论分析模型，进而推导出相应的参数估计算法。

在两个隐藏节点Xk=xi和Xk+1=xj设定为固定值的情况下，依据（给定）参数{P,Q}所得出的可见节点序列W 0,W 1,Wn的概率：

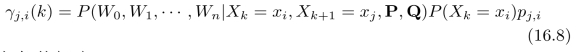
其中条件概率

为转移矩阵P中第j行、第i列的元素。事实上，给定的两个隐藏节点Xk=xi和Xk+1=xj将Markov链分为了两个子链，第一个子链包含k个未知的隐藏节点，以给定的隐藏节点Xk=xi结尾；第二个子链包含n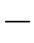k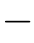1个隐藏节点，从给定的隐藏节点Xk+1=xj开始。因此，式(16.8)可以被进一步写成这两个子链的级联形式，也就是说，

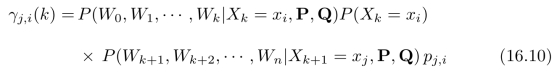
或者进一步将其写为：

剩下的问题是：如何计算式(16.11)中的两个子链的条件概率？注意，我们处理的是具有链式结构的概率图模型，参见图15.7。因此，我们可以采用递归的方式来逐步计算这两个子链的条件概率。

首先，我们令：

然后推导αj(m+1)和αi(m)之间的关系。根据定义，

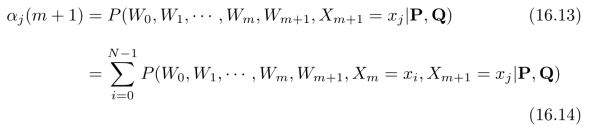
其中N为状态数目。进一步，可以计算：

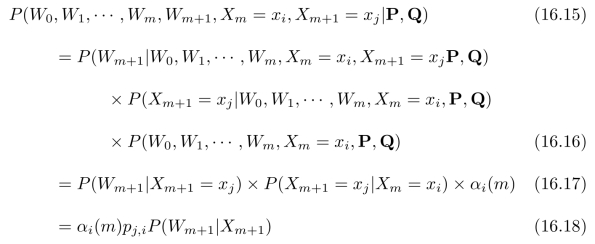
将上式代入式(16.14)，可以得到递推公式：

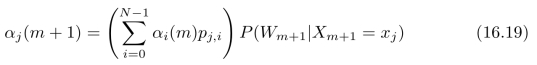
上式又称为前向递推算法。类似地，我们令：

然后推导βi(l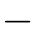1)和αj(l)之间的关系。根据定义，

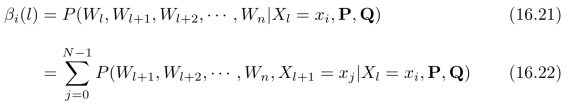
其中N为状态数目。进一步，可以计算：

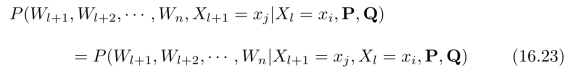
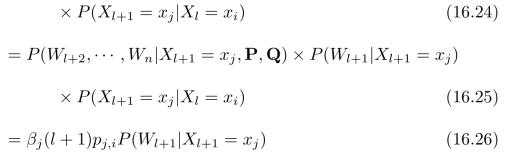
式(16.24)到(16.25)是根据图15.7所示的链式概率图结构而得出的，在已知X l+1=xj的情况下，W l和X l=xi对于确定W l+1不提供附加信息；另外，在已知X l=xi的情况下，W l和X l+1=xj是相互独立的，称为条件独立。将式(16.26)代入式(16.22)，可以得到递推公式：

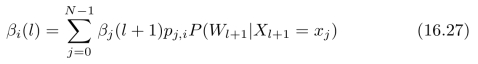
上式又称为后向递推算法。于是，式(16.11)可以被进一步写为：

首先，通过前向递推算法生成所有的αi(k)，结果保存成一个N×n的矩阵A；然后，通过后向递推算法生成所有的βj(k)，结果保存成一个N×n的矩阵B；最后，根据式(16.28)生成所有的γj,i(k)，保存成一个三维张量C或一个N 2×n的矩阵C。注意，k=0,1,2,···,n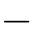1。在习题16.1中，我们将详细探讨αi(k)、βj(k)和γj,i(k)的算法实现过程，以及矩阵A、B和C的具体生成过程。

条件概率γj,i(k)给出了：在给定参数{P,Q}的情况下，每一对隐藏节点Xk→X k+1在不同状态之间跳转时所对应的一组可见节点序列W 0,W 1,···,Wm,Wm+1的条件概率。我们可以用这组条件概率来评判隐藏节点在不同状态之间的跳转，进而用于更新和调整转移矩阵P中的状态转移概率{pi,j}、初始节点X 0各个状态的概率分布（向量）p0以及Gauss分布中的均值和方差（即：Q中的参数）。

正如我们在上一小节中所分析的，参数{P,Q}的优化估计不存在解析求解过程，需要通过设计算法来实现。下一小节中，我们将详细讨论一种经典的参数估计方法：Baum-W elch算法。(www.xing528.com)

16.1.3　Baum-Welch算法

式(16.8)中的γj,i(k)定量地描述节点X k→Xk+1在不同状态之间跳转所带来的影响，也就是说，在两个隐藏节点X k=xi和Xk+1=xj设定为固定值的情况下，一组可见节点W 0,W 1,···,Wn对于给定参数{P,Q}的条件概率。进一步，我们可以通过计算：

来对γj,i(k)进行归一化，使得γj,i(k)/γi(k)成为一组归一化的系数，从而定量地分析和描述Xk状态变化的影响。进一步，我们可以将所有的{γj,i(k)/γi(k)}排列成矩阵，来作为对X k→X k+1在不同状态之间跳转所对应的转移矩阵的一种估计。进一步，同时考虑隐藏节点中的所有随机变量在不同状态之间的跳转，于是，我们可以将

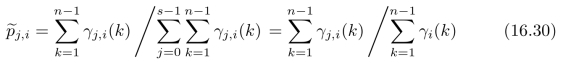
作为对转移矩阵中的条件概率pj,i的一种估计，其中s表示随机变量的状态数目。这一思想和后续推导出的方法就是著名的Baum-W elch算法。进一步，为对起始节点的状态分布的估计可以选为：

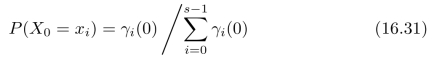
我们需要继续对Q中的参数进行估计。此时，状态xl也是未知的（其中l=0,1,2···,s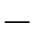1），需要对其进行估计。我们假设隐藏节点X k和可见节点Wk之间服从Gauss分布，也就是说，

待估计的未知量共2k个，包括xl和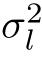，其中，l=0,1,2,···,s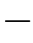1。这一任务相对简单一些，有很多现成的方法，例如：使用著名的k-m eans聚类算法对可见节点W 0,W 1,···,Wn的一组观测结果进行聚类。需要注意的是：对于我们的问题，γi(k)给出了对节点X k取各个状态的一种权重评估，但是，在k-means聚类算法中，却没有这一信息。因此，在k-means聚类算法中，每一个样本都“确定”地划归某一个类，但是，基于γi(k)，我们可以让每一个样本都按照比例被“分配”给所有的类。这样做的一个好处是：相当于大大增加了样本量，另外，还可以避免某一类的样本没有出现的极端情况。因此，Baum-W elch算法采用如下的参数估计方式：也就是说，以γl(k)/作为归一化权重进行加权平均。事实上，式(16.33)中的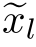和式(16.34)中的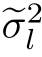是关于Gauss分布(16.32)中参数xl和σ2的最大似然估计结果。这是一个众所周知的结果。

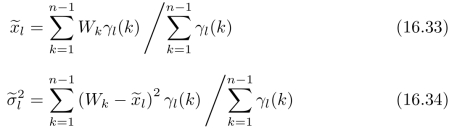
至此，我们估计出了参数{P,Q}，参见式(16.31)、(16.30)、(16.33)和(16.34)。但是，我们的任务还没有完成，因为在计算γj,i(k)和γl(k)的过程中需要用到参数{P,Q}。对于这类“鸡生蛋—蛋生鸡”的问题，我们自然想到了迭代计算，也就是说，

将上面的迭代进行下去，直到{P,Q}不再发生明显变化为止，就得到了Baum-W elch算法的输出结果{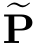,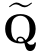}。我们可以直接使用Baum-Welch算法的结果{,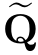}，或者，使用“蛮力法”在{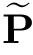,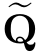}附近计算式(16.5)，进一步逼近{P*,Q*}。

图16.1中给出了一个实验仿真结果。图16.1(a)中给出了隐Markov模型中可见节点的一组观测结果。我们使用Baum-W elch算法进行10次迭代，所得到的参数估计结果为：

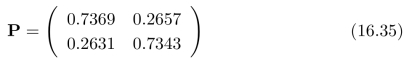
初始节点各个状态的概率估计结果为：

式(16.32)中Gauss分布的参数估计结果为：均值分别为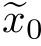=0.8049和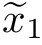=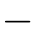0.3889，方差分别为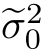=2.5415和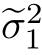=2.7506。依据上述参数估计结果，我们采用15.4小节中介绍的动态规划算法，即习题15.3中详细探讨的V iterbi算法，来直接得出最大后验估计结果，如图16.1(b)所示。对比图15.8，状态间的频繁跳动得到了有效抑制，在下一小节中，我们还会尝试对Baum-W elch算法进行一些新的调整。

16.1.4　条件最大后验估计

我们常常碰到的一种情况是：在通过隐Markov模型进行状态估计时，有些隐藏节点X k已经（根据可见节点Wn附近的几个观测结果）做了人为标注，也就是说，X k=xm是提前确定好了的，不允许更改。对于上述这种情况，我们在使用习题15.3中的V iterb i算法进行模型求解时，还必须确保“最优估计结果”序列中包含Xk=xm，但是，Viterbi算法无法确保这一点。

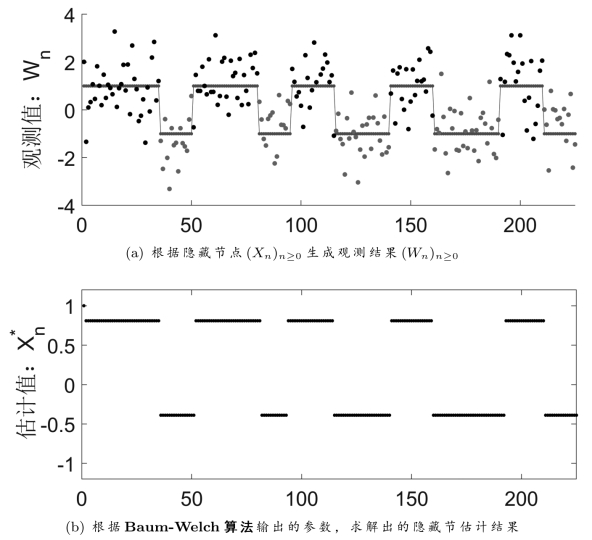
图16.1　隐Ma rkov模型实验结果。Ma rkov链(X n)n≥0只包含两个状态x0=+1和x1=-1。(a)可见节点与隐藏节点之间的服从标准正态分布。(b)根据B aum-W elch算法迭代30次后的参数求解出的估计结果。

本节中，我们将讨论如何求解Xk=xm固定时的“最优估计结果”序列，我们将其称为条件最大后验估计结果。首先，我们需要计算当Xk=xi和Xk+1=xj设定为固定值的情况下，通过动态规划算法所得到的“最优估计结果”序列,···,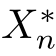所对应的后验概率：

上式可以进一步写为：

其中的定义参见式(15.73)，pj,i=P(Xk+1=j|X k=i)为相应的状态转移概率，为从X k+1=xj开始的后nk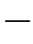1个状态X k+2,X k+2,···X n的最大后验概率，也就是说，

采用15.4小节中介绍的动态规划算法，可以直接求解，基本过程与求解一致。我们将通过习题16.2对其进行详细讨论。事实上，给定的隐藏节点X k=xm将Markov链分为了多个子链，对于每一个子链，在使用动态规划方法（即V iterb i算法）求解的过程中，还要确保起始节点的状态始终为xm保持不变。

基于上述分析，我们找到了一种方法去评估：某个节点Xk的状态变化对整个“最优估计结果”序列的影响。我们也可以尝试使用式(16.38)中的γj,i(k)来代替式(16.8)中所使用的γj,i(k)，然后，使用Baum-W elch算法中的参数估计公式(16.31)、(16.30)、(16.33)和(16.34)来更新{P,Q}。图16.2中给出了一个实验仿真结果。类似于图15.8(a)中的设置，Markov链(Xn)n≥0只包含两个状态x0=+1和x1=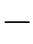1。可见节点Wn与隐藏节点X n之间的似然条件概率服从标准正态分布，也就是说，式(16.32)中的=1。此外，状态具有一定的持续性，也就是说，状态Xn=xk在时间段T（一个15到35之间的随机数）内保持不变，直到X n+T+1才跳转到新的状态，如图16.2(a)所示。为了便于观察，图16.2(a)中同时画出了(X n)n≥0和(Wn)n≥0，只有(Wn)n≥0是“可见的”，(Xn)n≥0只是用于对比仿真结果。

采用上面介绍的方法（将Baum-W elch算法中的γj,i(k)替换成式(16.38)中的γj,i(k)）进行参数估计，经过1次迭代，转移矩阵更新为：

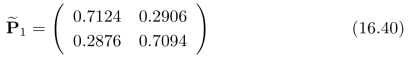
相应地，式(16.32)中，Gauss分布的均值估计结果更新为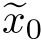=0.5610和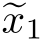=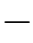0.6241，方差的估计结果更新为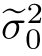=1.4158和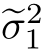=1.6405。继续进行迭代，到第9次迭代时，转移矩阵更新为：

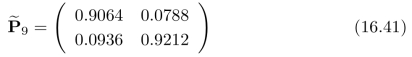
再次进行迭代计算，第9次迭代时的转移矩阵更新为：

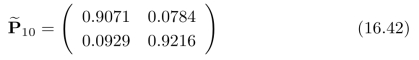
图16.2　隐Ma rkov模型实验结果。(a)实验数据。(b)根据参数估计算法迭代10次，用相应参数求解出的估计结果。(b)直接使用V iterb i算法的估计结果。

基本趋于稳定。此时，式(16.32)中，Gauss分布的均值估计结果更新为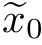=0.9517和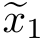=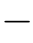0.7664，方差的估计结果更新为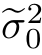=0.9308和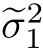=1.4326。作为对比，图16.2(c)中给出了直接用动态规划算法解出的隐Markov模型中隐藏节点的估计结果，参见15.4小节内容。求解过程中，相应的参数选为图16.2(a)中实验所对应的参数，也就是说，隐藏节点的状态也选为x0=+1和x1=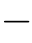1，式(15.79)中的参数选为σ2=1。实验中，我们将相应的转移矩阵设置为：

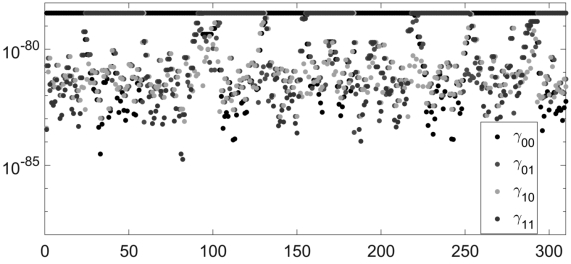
图16.3　第10步迭代时所得出的参数γj,i(k)，其中i,j=0,1，k=1,2,···310。

正如我们在图15.8中看到的，图16.2(c)中的最大后验估计结果与图16.2(a)中的(Xn)n≥0基本符合，但是状态之间存在一些频繁的跳转。

图16.3中给出了相应的γj,i(k)，其中i,j=0,1，k=1,2,···,310。可以看到，在优化结果中，γ0,0和γ1,1（在统计意义上）占“主导地位”，因此，在估计出的转移矩阵中，对角线元素p0,0和p1,1远大于非对角线元素。另外，注意观察图16.3中γj,i(k)在每一个k时的最大值，也就是说，图16.3中上方由红点γ0,0(k)构成的“线段”与由黑点γ1,1(k)构成的“线段”之间的排列模式，对比图16.2(c)中蓝色线段的排列模式，就不难理解为什么会取得图16.2(b)中的隐藏节点估计结果。注意，为了显示的方便，图16.3中的纵坐标采用对数形式，需要通过纵轴标尺刻度来衡量图16.3中点的真是取值。

16.1.5　解决下溢问题

从图16.3中可以看出，γj,i(k)的取值都非常小，范围在10-86到10-78之间，对于一些老式的计算机，γj,i(k)已经超出了其精度范围，随之将全部变为0，这种现象在数值计算中被称为下溢。随着链条长度n的增加，这一问题将变得愈发严重。因此，在计算过程中，我们对式(16.38)中的γj,i(k)取对数，记为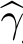γj,i(k)，也就是说，

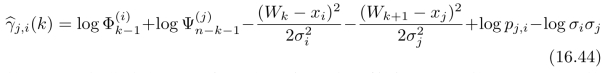
然后进行优化求解。注意，我们在后续计算中所需要的不是γj,i(k)的真实值，而是γj,i(k)相互之间的比例关系，参见式(16.30)、(16.33)和(16.34)。因此，我们可以对所有的γj,i(k)进行等比例放大。那么，究竟该放大多少呢？一个选择是：将γj,i(k)中的最大值放大为1，对其他的γj,i(k)进行同比例放大。相应地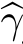，γj,i(k)中的最大值应该被增大到0。因此，我们首先计算：

然后对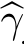γj,i(k)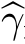γm ax进行指数运算，得到

将上式中的γj,i(k)代入式(16.31)、(16.30)、(16.33)和(16.34)中进行计算，可以得到相同的参数估计结果，同时避免了数值计算过程中的下溢问题。需要指出的是：Baum-W elch算法无法采用上述方式来解决下溢问题。注意，在前向递推公式(16.19)和后向递推公式(16.27)中，都存在“相加”和“相乘”的项，通过“取对数”，可以把“相乘”的项拆分出来，但是，无法对“相加”的项进行处理。通过采用（上一小节提出的）基于条件最大后验估计的参数估计方法，也就是说，将Baum-W elch算法中的γj,i(k)替换成式(16.38)中的γj,i(k)，然后代入式(16.31)、(16.30)、(16.33)和(16.34)中进行参数更新，我们成功地解决了上述问题。此时，前向递推公式(16.19)和后向递推公式(16.27)中的“相加”项被转换成了“求最大”（参见式(15.75)和(16.53)），使得连乘的形式得以维持，因此，可以通过（本小节中所介绍的）“取对数”的方式来解决下溢问题。