隐马尔可夫模型Viterbi算法实现及仿真结果分析

习题15.1假设在第n次操作时，单位投入的回报比例τn满足：

其中p∈(0.5,1)，并且，τ1,τ2,···之间相互独立。经过第n次操作后，你的总资产为X n，因此，在第n次操作中，你动用的资金Yn介于0和X n-1之间。你的目标是：使得投资回报率的数学期望E(log(XN/X 0))最大，其中N表示给定的操作次数，一开始的资产X 0为常数。相应的过滤子选为Fn=σ(τ1,τ2,···,τn)。如果(Yn)n≥1是固定策略的随机过程，也就是说，对于所有的n≥1，都有Yn在Fn-1下可测，请证明：随机过程(log X n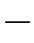nα)n≥0是一个超鞅，其中

其中q=1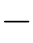p。进一步，请证明：

请找到一个最优策略(Yn)n≥0，从而使得随机过程(log X n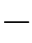nα)n≥0构成一个鞅。

习题15.2请设计一个仿真程序，完成图15.1中随机游走的仿真实验，基本过程如下：

1.生成一个服从均匀分布的随机整数序列(Yn)n≥1，随机整数的取值为+1和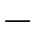1，并且，

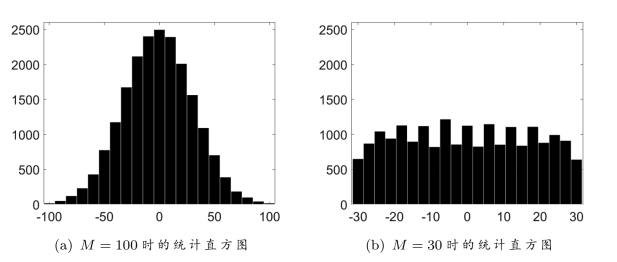
图15.11　对于图15.1(a)中的随机游走的仿真结果，参数N=1000、m=20000。(a)当M=100时，关于X N的统计直方图。(b)当M=30时，关于X N的统计直方图。

2.初始值设为X 0=0，然后，对(Yn)n≥1求和

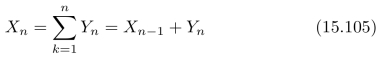
生成一组新的随机变量X 1,X 2,···,XN。

3.重复上述操作m次，对所得到XN的m个仿真结果做统计，来估计随机变量XN的概率分布。

在此基础之上，我们来考虑边界条件，需要对上述过程做一些小的调整。对于图15.1(a)中的随机游走，当X n=M时，将Yn+1调整为：

当Xn=+M时，将Yn+1调整为：

对于图15.1(b)中的随机游走过程，当Xn=M时，令Yn+1=0。

请分析M取不同值对仿真结果的影响。例如，对于图15.1(a)中的随机游走过程，我们取N=1000、m=20000，仿真结果如图15.11所示。当M较大时（例如M=100），图15.11(a)中关于XN的统计结果有什么特点？当M较小时（例如M=30），图15.11(b)中关于XN的统计结果有什么特点？请给出理论分析，完成实验报告。

习题15.3本题中，我们将探索隐Markov模型的算法实现过程。在15.4小节中，我们详细介绍了通过动态规划算法求解最大后验估计的基本思想和理论分析，本题中，我们将从算法实现的角度来详细探讨求解过程，即著名的V iterb i算法。

(a)首先，我们对15.4小节中的迭代过程做一下总结。我们需要不断维护和更新两个“最优估计结果”序列：

以及上面两个“最优估计结果”序列所对应的后验概率：

式(15.108)中序列的初始条件为x0和x1，对应的后验概率为：

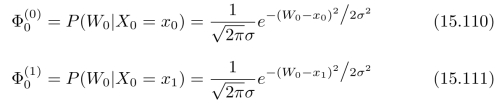
后验概率（其中i=0,1）的更新过程为：

其中pi,j=P(Xn=xi|Xn-1=xj)可以直接在转移矩阵中查找得到。请写出迭代更新算法，并编写程序实现仿真。

(b)现在，让我们来更新式(15.108)中的“最优估计结果”序列。在求解式(15.112)的极值后，同时保存式(15.112)的极值解

然后，在式(15.108)中的两个“最优估计结果”序列中，找到以结尾的序列，从而将“最优估计结果”序列更新为：

我们接下来要设计上述过程的具体实现方式，也就是说，根据给定的xj在式(15.108)中的两个“最优估计结果”序列中，找到以xj结尾的序列，进而将“最优估计结果”序列更新为(15.114)，再进行存储。请写出迭代更新算法，并编写程序实现仿真。

(c)式(15.108)中的两个“最优估计结果”序列的更新过程比较烦琐，需要在迭代过程中的每一步都维护、更新和存储两个链表。此外，两个链表之间可能存在“合并”，也就是说，在第k次迭代中，出现X k+1=x0和X k+1=x0前面节点相同的情况，从而导致前面的Xk+1=x0和Xk+1=x0前面的链表完全一样。此时，对另一个链表的前期维护工作事实上是不需要的，但是，为了后续迭代，另一个链表还需要被继续维护下去。一个相对简洁的处理方式是：每次迭代后，只记录式(15.113)中优化结果的状态xj的下标j，从而形成两个索引列表L0和L1。在每次迭代中，列表L0的最后一个元素都是0，表示以x0结尾；而列表L1的最后一个元素都是1，表示以x1结尾。我们甚至可以将这两个索引列表合在一起，以矩阵的形式进行存储：

也就是说，将索引列表L0和L1分别作为矩阵L的第一列和第二列，如图15.12(b)所示。

在完成迭代计算后，我们需要通过遍历矩阵L，来最终生成最大后验估计结果

这个过程是从后往前递推的，称为回溯。首先，根据的状态的下标i，找到索引列表Li；然后，查找索引列表Li中的第n1个元素j；进而确定的状态xj。重复上述过程，就可以生成式(15.116)中的最大后验估计结果。

请写出迭代更新算法，并编写程序实现仿真。进一步，请证明：“回溯”过程所得到的结果与（本题(b)问中介绍的）通过维护两个链表所得到的结果是一样的。

图15.12给出了一个实验仿真结果。图15.12(b)中给出了：通过“向前”更新迭代而生成的两个索引列表L0和L1。然后，根据两个索引列表L0和L1“向后”回溯，最终得到的最大后验估计结果如图15.12(c)所示。请在(a)、(b)、(c)三个问题的基础上，编写程序实现图15.12中的仿真，并对选取不同参数的情况进行对比分析，完成实验报告。(www.xing528.com)

习题15.4对于图15.9所示的Bayes网络，在通过动态规划算法实现最大后验估计的过程中，一个核心的问题是：如何维护众多备选的“最优估计结果”序列

不同于隐Markov模型，上面每一个“最优估计结果”序列都是通过给定k个编号in-k+1,in-k+2,···,in来进行索引的。

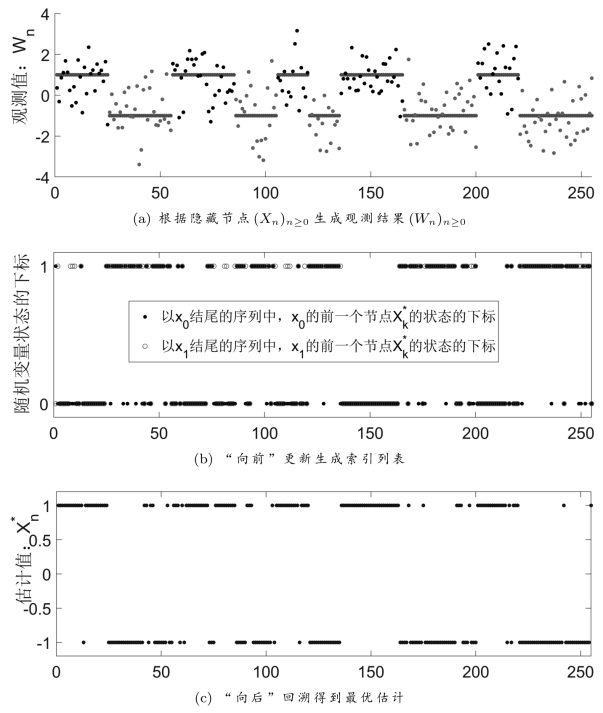
图15.12　V iterb i算法的实现过程演示。(a)实验数据。(b)根据迭代算法“向前”更新，形成两个索引列表L 0和L 1。(c)根据索引列表“向后”回溯，得到最优估计结果。

(a)假设随机变量Xn共有s个状态x0,x1,···,xs-1，也就是说，对于任意的l，下标il共有s个可能的取值0,1,2,···,s1。于是，我们需要维护sk个“最优估计结果”序列。我们需要定义一个十进制的数：

来指定和查找式(15.117)中的“最优估计结果”序列所对应的“指针”或“索引值”。

进一步，当给定十进制数后，我们可以通过模运算迭代，找到对应的k个索引编号in-k+1,in-k+2,···,in。首先，

也就是说，除以s的余数。然后计算：

继续计算下去，直到求出in为止。请写出具体算法模块，实现（十进制数）指针与（k位s进制数组成的）索引编号in-k+1,in-k+2,···,in之间的相互转换。

(b)现在，我们对指针列表进行遍历，逐一进行更新。根据某一个给定的指针，首先通过模运算迭代，找到对应的k个索引编号，与之相对应的“最优估计结果”序列为：

在更新前的指针列表中，以结尾的索引编号所对应的指针总共有s个。首先，我们需要找到这s个指针，然后，根据式(15.97)选出一个，作为更新结果。这s个的指针所对应的（由k位s进制数组成的）索引编号为z,，其中，是固定的，z分别取0,1,···,s1，就找到了对应的s个备选的索引编号。进一步，根据式(15.118)可以计算出对应的s个指针

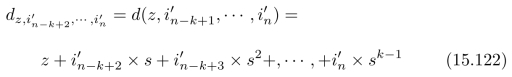
然后，根据这s个指针找到相应的数据，代入式(15.97)中进行计算，从而确定z的取值z*，完成指针更新过程：

请写出具体算法模块，实现指针之间的对应查找和更新过程。

(c)事实上，通过使用一些数学技巧，可以优化上述指针之间的对应查找和更新过程，从而避免十进制数和s进制数之间的相互转换。注意，式(15.118)中的后k1位s进制数始终保持不变，如果我们可以通过十进制数直接得出：式(15.118)中的后k1位s进制数所对应的十进制数，那么，我们就可以直接计算出（式(15.118)中z分别取0,1,···,s1时所对应的）s个指针。事实上，通过模运算可以建立两者之间的联系。根据

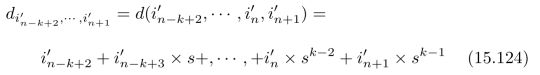
可以进一步计算得到：

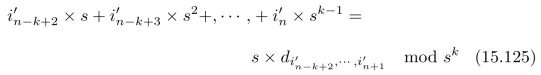
对比(15.122)可以发现：

最终，我们实现了对指针列表的直接维护更新。当s=2,k=3时，初始指针列表为：

根据式(15.126)，每一个指针都有两个备选的更新值，即下表相应列中的两个元素：

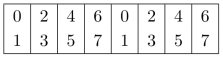
根据这两个指针找到相应的（两组）数据代入式(15.97)中进行计算，在这两个指针中确定一个最优选择，从而完成指针列表的更新。假设更新结果如下：

根据式(15.126)，继续计算每一个指针的两个备选的更新值

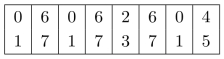
根据上表中每一列的两个指针找到相应的两组数据代入式(15.97)中进行计算，从而在这两个指针中确定一个最优选择，进而完成新一轮的指针列表更新。请写出具体算法模块，并且，对k=3,4,···的情况进行仿真，进而和图15.10中的结果进行对比分析，完成实验报告。

注意，由于我们的s个下标选为0,1,2,···,s1，因此，式(15.118)和(15.124)才成立，如果我们将s个下标选为1,2,···,s，那么，式(15.118)和(15.124)将不再确保成立。这是设计仿真程序时的一个常见问题。

【注释】

[1]关于“几乎确定”的定义和具体解释，参见式(14.90)。

[2]Monte Carlo是摩纳哥的一个著名赌场，用在这里就是指随机采样。—王亮

[3]在Metropolis 1954年提出的原创性算法中，所有的ci,j=1。Hasting对Metropolis的工作做出了改进，提出了式(15.52)。当然，我们的假设条件“只能进行均匀分布采样”可以适当放宽，例如：可以采样出高斯分布样本，此时，式(15.51)将变得更加复杂，高斯分布的函数qj,i和qi,j将被引入。

[4]关于概率图模型相关详细内容，我们推荐CMU的课程Probabilistic Graphical Models和MIT的课程Introduction to In ference。

[5]注意，式(15.59)中的后验概率分布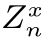同时也是一个随机变量。

[6]也就是说，令式(15.78)中的σ=1。虽然有多种方式生成(W n)n≥0的样本集，但是我们建议使用15.2小节中介绍的MCMC采样算法，来回顾15.2小节内容。

[7]这项工作由加州大学洛杉矶分校的Pearl教授于1985年首次提出，更多详细内容可以参见文献Pearl,J.(1988).Probabilistic Reasoning in In telligen t System s:Networks of P lausible Inference.San Mateo,CA:Morgan Kau fm an.