Bayes网络的应用与优势

在很多应用中，随机过程(X n)n≥0的状态具有一定的“持续性”，不会太过频繁地跳动，如图15.8(a)所示。对于这种情况，更新过程(15.63)中的随机变量Yn+1不再是仅仅取决于随机变量Xn的取值，还与前面的k1个随机变量Xn-1,Xn-2,···,X n-k+1有关。此时，各个状态之间相互转移的条件概率

不再是一个矩阵，而是一个k+1维的张量P，其中的元素

事实上，张量是一个高维矩阵，而矩阵是一个二维张量。矩阵可以看作是一种“数据管理方式”，根据下标（或索引）(m 1,m0)对数据集中的某一个数进行查找。对于矩阵，下标（或索引）由两个数组成，分别对应于矩阵的行标和列表，用于查找矩阵中的元素。对于k+1维张量，下标（或索引）(m k,m k-1,···,m0)由k+1个数组成，用于查找张量P中的元素。此时，概率图中的隐藏节点(X n)n≥0不再具有链式结构，如图15.9所示。

在图15.9中，共有3条件边“指向”隐藏节点X 3，此外，还有另外3条件边“指离”隐藏节点X 3。我们首先需要定义这些边和条件概率之间的对应关系：所有“指向”同一节点X 3的三条边X 0→X 3、X 1→X 3和X 2→X 3合在一起，共同确定了关于X 3的条件概率P(X 3|X 2X 1X 0)；某一条“指离”隐藏节点X 3的边（例如X 3→X 4）配合另外两条边X 2→X 4和X 1→X 4，从而最终确定了所指向的节点X 4条件概率P(X 4|X 3X 2X 1)。

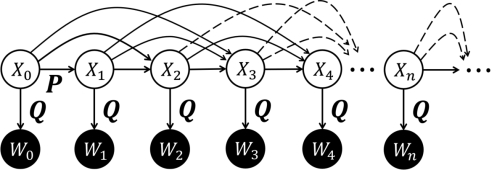
图15.9　对于更复杂的随机过程，状态的更新不仅仅取决于当下的随机变量，还与前面的多个随机变量有关。此时，概率图模型不再具有链式结构。在B ayes网络中，指向同一节点X n的所有边Xm 1→X n,Xm 2→X n,···,Xm k→X n共同确定关于X n的条件概率P(X n|Xm 1 Xm 2···Xm k)。通过上述规则，Bayes网络将具有链式结构的概率图模型，例如隐Markov模型，拓展到更一般的有向图上。

注意，只有当某一个节点被唯一的箭头（有向的边）所指向时，才存在箭头两端两个节点之间的条件概率。例如，在概率图15.9中，存在条件概率P(X 1|X 0)和P(Wn|Xn)，但是，不存在条件概率P(X 2|X 1)，因为节点X 2是由节点X 1和X 0共同确定的。

通过上述方式，我们建立起了一种有向图和概率分析之间的对应关系，称为Bayes网络^[7]。Bayes网络通过定义如下规则：

•指向同一节点Xn的所有边Xm 1→X n,Xm 2→Xn,···,Xm k→Xn共同确定关于Xn的条件概率P(Xn|Xm 1 Xm 2···Xm k)。

将具有链式结构的概率图模型，例如隐Markov模型，拓展到更一般的有向图上。具有链式结构的图中不存在环，Bayes网络中也不允许出现环。对于随机过程(15.63)，这一点是得到保障的。

我们的任务仍然是根据一组可见节点W 0,W 1,···,Wn来估计隐藏节点X 0,X 1,···,Xn。估计方法仍然是最大化后验概率：

根据Bayes公式，可以进一步得到：

在图15.9所示的Bayes网络中，似然条件概率为：

同样，概率P(W 0W 1W 2···Wn)只起到归一化的作用，不影响极值问题(15.87)的求解结果，参见15.4小节中的分析。于是，极值问题(15.87)可以进一步写为：

注意，图15.9所示的Bayes网络不再具有链式的概率图结构，因此，先验概率P(X 0X 1···Xn)不再具有式(15.55)中的表达形式。为了求解最大后验估计结果我们首先需要推导出先验概率P(X 0X 1···Xn)的具体形式。

对于图15.9中的概率图模型，

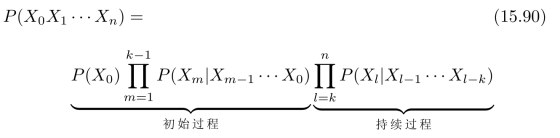
每一个随机变量X l的状态转移概率，都依赖于前面k个随机变量X l-1,X l-1,···,X l-k的状态。示意图15.9中k=3，在这里我们讨论更一般的情况，不具体化k的取值。最终，我们得到了最大似然估计(15.89)中优化目标的具体形式：

在实际操作中，我们可以对“初始过程”做一些简化，例如，先用15.4小节中介绍的隐Markov模型运行m步（并且m＞k），然后，从第m+1步开始使用Bayes网络模型。此时，最大似然估计问题为：

(www.xing528.com)

前m步隐Markov模型的运行结果将作为已知条件，直接用于求解式(15.92)。

如同我们在15.4小节中所分析的，式(15.92)的求解是一个不断更新的过程：在的基础上，依据新引入的观测结果Wn，来更新极值问题(15.92)的解。自然地，我们想到用动态规划来进行求解。

在隐Markov模型的求解过程中，对于随机变量Xn的每一个可能的取值xi，都需要维护一个以xi结尾的“最优估计结果”序列，参见15.4小节中的分析。对于Markov链，随机变量Xn+1的取值仅依赖于随机变量X n，但是，对于图15.9所示的Bayes网络，随机变量Xn+1的取值同时依赖于前面的k个随机变量X n,Xn-1,···,X n-k+1。因此，不难想象，对于这k个随机变量序列X n-k+1,Xn-k+2,···,X n的每一组可能的取值xin-k+1,xin-k+2,···,xin，都需要维护一个以xin-k+1,···,xin结尾的“最优估计结果”序列：

每一个最优估计结果都对应于一个索引，相应的极值记为：

求解优化问题(15.92)就是去选定式(15.93)中的(xin-k+1,···,xin)，也就是说，

然后根据从众多的“最优估计结果”序列

中取出以结尾的序列，作为更新后的最大后验估计结果。

根据新引入的Wn，我们需要对(15.93)中的“最优估计结果”序列进行更新，也就是说，对于所有可能的(xin-k+2,···,xin+1)，都需要求解：

然后，将以结尾的序列与相应的子序列（已具体给定）xin-k+2,···,xin+1合在一起，最终形成更新后的序列：

进一步，根据式(15.97)所求出的最优解，我们需要对极值进行更新，以便继续求解(15.95)。根据式(15.73)，不难发现的更新规则：

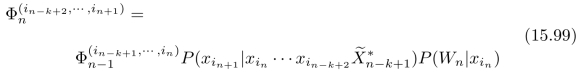
当Wn+1被引入后，根据更新后的极值，可以从更新后的“最优估计结果”序列中继续挑选出更新后的最大后验估计结果，参见式(15.95)。当k=1时，上述过程相应地退化成了隐Markov模型。

条件概率所组成的张量P可以用“矩阵集合”的形式进行存储。例如，对于图15.8(a)所示的实验，当k=2时，张量P={P 1,P2}中包含两个2×2的矩阵。图15.10中给出了

时的实验结果。矩阵P i的下标i表示随机变量X n+1的状态xi的下标i。矩阵P i中元素pj,k的行标j表示随机变量Xn的状态xj的下标i，列表k表示随机变量Xn-1的状态xk的下标k。较之于Markov链中的转移矩阵(15.81)，式(15.100)更细致地描述了关于“状态转移特性”的先验信息。图15.10(a)中的参数设置与图15.8(a)中的设置完全相同，然后，选取参数σ=1进行最大后验估计。虽然k=2时的Bayes网络只比隐Markov模型（k=1时的情况）多考虑了一个隐藏节点，但是，一部分（由于随机噪声引起的）频繁状态跳动已经得到了有效抑制。

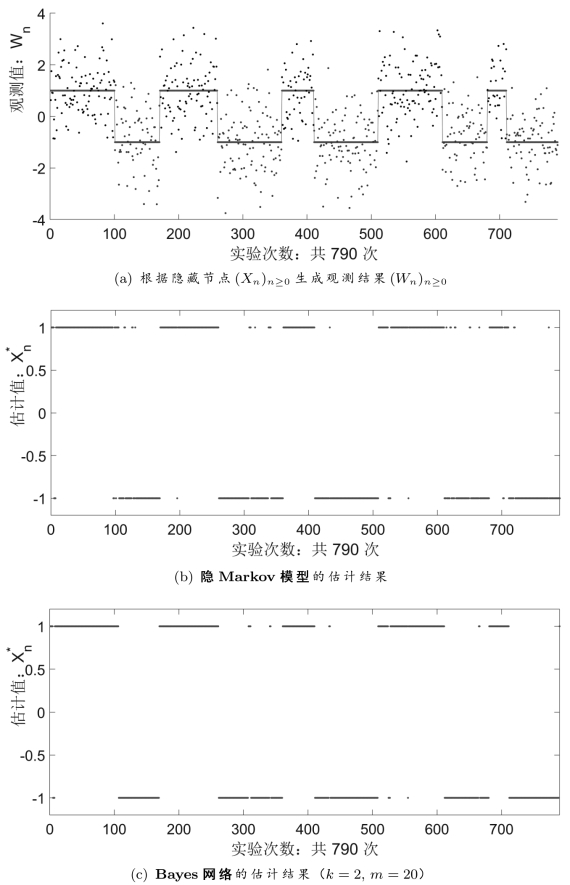
图15.10　隐Markov模型与Bayes网络的实验结果对比。隐Markov模型的转移矩阵选为式(15.81)，Bayes网络的条件概率张量选为式(15.100)。

较之于隐Markov模型，图15.9所示的Bayes网络的计算量要大很多，此外，还需要更多的存储容量。假设随机变量Xn有s个不同的状态，在隐Markov模型的求解过程中，需要维护s个“最优估计结果”序列，但是，在（图15.9所示的）Bayes网络的求解过程中，却需要维护sk个“最优估计结果”序列。在迭代更新的过程中，隐Markov模型每次只需要进行O(s)次计算，但是，（图15.9所示的）Bayes网络却需要进行O(sk)次计算。虽然Bayes网络在计算和存储上需要付出额外的开销，但是，却增强了系统的鲁棒性，有效抑制了单次判断失误或随机噪声所引起的频繁状态跳转，参见图15.10。

当然，概率图模型的内容远不止于此。在习题15.4中，我们将进一步探讨算法实现中的一些细节问题。我们介绍概率图模型的相关内容，是为了对教学课堂中的学生专注度进行分析（参见第16章的内容）。因此，本章只详细探讨了图15.9中所示的一种特殊的Bayes网络模型。