隐Markov模型的应用及实现

上一小节中，我们给出了两个具有链式结构的概率图模型，分别对应于前面详细分析过的两个随机过程：Markov链和P´olya罐子实验。这两个随机过程都是单步更新过程：

也就是说，更新过程中的随机变量Yn+1只依赖于Xn，而与X 0,X 1,X 2,···,X n-1无关，因此，这两个随机过程都具有链式的概率图结构。概率图15.5也很好地描述出了这两个随机过程之间的区别：条件概率矩阵（或转移矩阵）是否始终保持不变。我们还谈到，有些随机变量是可观测的，有些随机变量无法直接进行观测，只能进行“推测”，如图15.6所示。

将上述两个特点结合在一起，我们就得到了隐Markov模型，如图15.7所示。隐Markov模型首先是一个Markov链(Xn)n≥0，具有固定的转移矩阵P，其中第l行、第k列的元素为：

也就是说，在事件Xn=k的情况下，事件Xn+1=l的条件概率。与Markov链不同的是，随机变量Xn是无法被直接观测的，只能观测到与Xn相关的另一个随机变量Wn，例如，Xn表示选用不同的骰子，Wn表示实验结果序列。类似地，这两个随机变量Xn和Wn通过条件概率矩阵Q联系在了一起，其中第l行、第k列的元素为：

图15.7　隐Markov模型是一个Ma rkov链(X n)n≥0，具有固定的转移矩阵P。与Markov链不同的是，一组随机变量{X n}是无法被直接观测到的（例如是否偷偷更换骰子），只能观测到与{X n}相关的另一组随机变量{W n}（例如抛骰子的实验结果序列）。条件概率矩阵Q对应于连接两个节点X n和W n的一条边。注意，从节点X n到节点W n的边是单向的，因为随机变量X n无法被观测，只能被推测。

也就是说，在事件Xn=k的情况下，事件Wn=l的条件概率。在概率图模型中，条件概率矩阵Q对应于连接两个节点（随机变量）Xn和Wn的一条边。注意，从节点Xn到节点Wn的边是单向的。随机变量X n无法被观测，因此，我们无法通过Wn得出X n，只能通过Wn推测出：Xn的后验概率分布或最优估计结果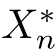，参见图15.6。

在图15.7所示的隐Markov模型的概率图中，可直接观测的一组随机变量{Wn}称为可见节点，无法直接观测的一组随机变量{Xn}称为隐藏节点。我们的一个重要任务是：根据一组可观测的随机变量{Wn}来推测出无法直接观测的一组随机变量{X n}，也就是说，根据概率图15.7中的可见节点来估计图中的隐藏节点。

解决上述问题的一种方法是：首先，求解条件概率

然后，通过最大化条件概率(15.66)来估计隐藏节点，也就是说，

我们将逐步解决上述两个问题。首先，根据Bayes公式，可以得到：

在式(15.68)中，P(X 0X 1X 2···X n)为：整条Markov链的概率（参见式(15.55)），也就是说，

在概率图15.7中，从节点Xk到Wk的（单向）边相互之间是不联通的，也就是说，条件概率P(Wk|Xk)相互之间是独立的（其中k=0,1,2,···），因此，式(15.68)中的

概率P(W 0W 1W 2···Wn)只起到归一化的作用，不影响极值问题(15.67)的求解结果。于是，极值问题(15.67)可以进一步写为：

式(15.69)中的P(X 0X 1X 2···Xn)与观测结果{Wk}无关，称为先验（概率）。式(15.70)中的条件概率P(W 0W 1W 2···Wn|X 0X 1X 2···X n)称为似然（概率），描述了{X k}和{Wk}之间的关联关系。式(15.68)中的P(X 0X 1X 2···X n|W 0W 1W 2···Wn)称为后验（概率），是依据观测结果{Wk}对隐藏节点{Xk}的估计。式(15.71)中的极值解被称为最大后验估计（结果）。

现在，我们来探索如何求解极值问题(15.71)。求解(15.71)的过程中，我们将{Wk}看作是常数，然后对{Xk}进行优化求解。注意，极值解是一个序列，随着实验不断进行，这些序列也在不断增加，也就是说，优化问题(15.71)是一个迭代更新过程，随着新观测数据Wn+1的引入，应该如何更新已经求得的最大后验估计结果，从而生成一组新的优化估计结果？熟悉算法的朋友可能会立刻反应过来，上述过程是一个动态规划。

事实上，动态规划方法是最常用的算法之一。当我们对求解一个“大问题”一筹莫展时，我们改而研究：如何通过求解一个“小一点”的相同问题，来求解这个“大问题”；进而，将求解这个“小一点”的问题转化为：求解一个“更小一点”的相同问题；将上述过程进行下去，直到将问题递归“约减”到我们能够解决的情况；最后，从能够解决的问题开始，逐步进行求解，直到“大问题”得到解决。

根据前n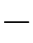1次的观测结果所求得的最大后验估计还不足以求出极值问题(15.71)的解。随着Wn的引入，相应地，可能发生变化。因此，对于随机变量X n的每一个可能取值xm，都需要找到一个对应的（根据前n1次的观测结果得到的）最优解，也就是说，

每一个xm都对应着一个估计结果“序列”，相应的极值记为：(www.xing528.com)

优化问题(15.71)的求解就是要去选定(15.73)中的xm，也就是说，

然后根据从众多的“最优估计结果”序列中取出以结尾的序列，作为新的最大后验估计。

我们的工作并没有结束，还需要将(15.73)中的“最优估计结果”序列更新为。通过求解：

可以确定以结尾的序列进而和xm一起最终形成更新后的序列。式(15.73)中的则相应地更新为

其中xm′是式(15.75)的最优解。对于有限状态（离散随机变量Xn的取值为有限个离散值）的Markov链，只需对式(15.74)和(15.75)中所有可能的取值进行遍历，然后根据极值解进行状态更新。对于包含无限个状态的Markov链，可以通过设置转移矩阵P，从而使得每次更新都只在有限的几个状态中进行跳转，例如，可以令

为一个“条带形”矩阵（又称为有界带宽矩阵）。此时P中元素的下标不再是元素在矩阵中的位置，而是矩阵中对角线的编号。对于任意的m和n，都有条件概率pm,n=pn-m。

我们常常将条件概率P(Wn|X n)设置为以Xn为中心的Gauss分布（或正态分布）：

此时，优化问题(15.74)可以进一步变为：

初始问题为：

相应的解为：与W 0最接近的值。事实上，式(15.79)给出了一种判定“状态跳转”的依据：除了考虑数据信息(WnX n)2外，还有状态跳转所需付出的“代价”。在习题15.3中，我们将详细讨论上述动态规划过程的算法实现方式，即著名的V iterbi算法。该算法在动态规划的更新过程中，巧妙地实现了：对以式(15.79)中结尾的序列进行有效维护、更新和存储。

图15.8给出了一个仿真实验。Markov链(Xn)n≥0只包含两个状态x1=+1和x2=1。可见节点Wn与隐藏节点Xn之间的似然条件概率选为标准正态分布^[6]。假设状态具有一定的持续性，也就是说，状态X n=xk在时间段T（10到100之间的随机数）内保持不变，直到Xn+T+1才跳转到新的状态，如图15.8(a)所示。为了便于观察，我们在图15.8(a)中同时画出了(Xn)n≥0和(Wn)n≥0。只有(Wn)n≥0是“可见的”，(X n)n≥0只是用于对比仿真结果。根据观测结果(Wn)n≥0，我们通过隐Markov模型来估计隐藏节点(Xn)n≥0的状态变化过程。针对“状态具有一定的持续性”这一先验信息，我们设置转移矩阵P使得：保持现有状态具有更高的概率，例如：

图15.8(b)给出了：式(15.79)中σ=1时的隐Markov模型估计结果。最大后验估计与图15.8(a)中的(Xn)n≥0基本符合。适当增加先验信息的权重，例如，令式(15.79)中的σ=2，可以进一步抑制状态之间的跳转，如图15.8(c)所示。

图15.8　根据观测结果(W n)n≥0，我们通过隐Ma rkov模型来估计隐藏节点(X n)n≥0的状态变化过程()n≥0。Ma rkov链(X n)n≥0只包含两个状态x1=+1和x2=-1。(a)可见节点W n与隐藏节点X n之间的似然条件概率选为标准正态分布。(b)σ=1时的隐Ma rkov模型估计结果()n≥0与(X n)n≥0基本符合。(c)适当增加先验信息的权重（σ=2）可以进一步抑制状态之间的跳转。

当然，我们也可以选取不同的似然函数，例如Lap lace分布：

此时，动态规划算法中的更新过程(15.79)相应地变为：

当Wn与X n偏差较大时，|WnXn|＜(WnX n)2，因此，较之于式(15.79)，更新过程(15.83)对数据的敏感程度要“迟钝”一些，相应地，状态之间的跳动也会相对“缓和”一些。