链式概率图模型简介

概率图模型的内容非常丰富，需要通过一门课程来讲解部分相关内容^[4]。本小节中，我们结合具体的应用实例来介绍相关理论、方法和思想。顾名思义，“概率图”就是将“概率分析”和“图”结合起来。“图”里面包含边和节点。正如我们在14.2小节中所讨论的，“概率分析”是围绕概率空间和随机变量进行的。于是，我们不难想象“概率分析”和“图”之间的结合方式：

•“图”中的节点对应于随机变量，“图”中的边对应于（随机变量之间的）条件概率。

边连接两个节点，而条件概率描述两个随机变量之间的相互关系。“概率图”模型以图的形式将随机变量之间相互关系描述了出来。注意，图15.1中所示的并不是概率图。图15.1中的节点不是随机变量，而是随机变量的取值（也称为状态），因此，图15.1中所描述的是（Markov链的）状态转移图，而不是概率图。

我们通过一些例子来逐步往下进行探索。对于一个Markov链，前n次实验结果为的概率为：

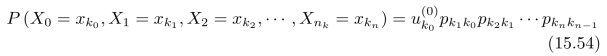
也就是说，随机变量Xk之间的关系满足

因此，Markov链（一个特殊的随机过程(X n)n≥0）中的各个随机变量X n之间形成了图15.5(a)所示的链式结构，称为Markov链的概率图。图15.5(a)中的转移矩阵P（参见式(15.11)）始终保持不变，这也是Markov链的一个基本特征。

对于14.7.3小节中讨论的P´olya罐子实验，随机过程(Wn)n≥0中的随机变量（抓到白球的次数）Wn序列也构成一个链式的概率图结构，如图15.5(b)所示。此时，转移矩阵P n随着n而不断发生变化。

转移矩阵P n中只有第1到第n+1列中含有非零元素（n从0开始），其他列中元素全为零。在第k+1列中（其中k≤n也是从0开始），只有两个非零元素pk+1,k+1和pk+2,k+1，分别位于第k+1行和第k+2行，具体取值为：

图15.5　在概率图模型中，节点对应于随机变量，边对应于（随机变量之间的）条件概率。(a)Markov链(X n)n≥0中的随机变量X n之间形成了一种链式的概率图结构，转移矩阵P始终保持不变。(b)Pˊo lya罐子实验中，抓到白球的次数(W n)n≥0也构成一个链式的概率图结构，但是，相应的转移矩阵P n随着n的增加不断发生变化。(c)后验概率分布{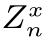}与实验结果{W n}之间存在一一对应的关系，也就是说，随机变量和W n之间的条件概率构成一个单位矩阵I。

也就是说，在Wn=k的情况下，事件Wn+1=l的条件概率，参见14.7.3小节中的分析。通过计算：

(www.xing528.com)

图15.6　一部分节点所对应的随机变量是可观测的，剩余的节点并不是直接观测得到的，而是（根据观测结果）推测出来的。(a)随机变量{W n}可以通过随机过程(W n)n≥0实验直接观测得到，而后验概率分布{}是依据{W n}推测出来的。(b)使得{}最大的x=也是一个随机变量，称为（基于一组可观测的随机变量的）最大后验估计。

不难发现转移矩阵P n随着实验次数n的变化规律。在14.7.3小节中，我们证明了，对于任意x∈[0,1]，由后验概率分布构成的随机过程是一个鞅^[5]。当x固定时，式(15.59)中的随机变量和Wn之间存在一一对应的关系，也就是说，随机变量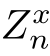和Wn之间的条件概率构成一个单位矩阵I，如图15.5(c)所示。注意，图中15.5(c)节点和Wn之间的边是双向的，因此，和之间是连通的，也就是说，→Wn→Wn+1→。

从图的观点出发，我们可以将图15.5(c)中的节点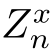和Wn互换（其中n=0,1,2,···），整个概率图的拓扑结构不发生变化。因此，随机过程()n≥0中的随机变量（白球比例的后验概率分布）序列也构成一个链式的概率图结构，如图15.6(a)所示。

图15.5(c)和图15.6(a)具有完全相同的拓扑结构。我们将图15.6(a)中的节点Wn（其中n=0,1,2,···）标注成黑色，是为了强调：节点所对应的随机变量Wn是可观测的。剩余的节点（其中n=0,1,2,···）并不是直接观测得到的，而是根据观测结果Wn，通过式(15.59)计算出来的。相应的过程被称为推理。

后验概率分布=p(x|Wn)是根据随机变量Wn的取值（实验观测结果）而生成的一个关于x的函数，我们更感兴趣的是：后验概率分布关于x的最大值：

式(15.59)对x求导，再令导数等于零。可以进一步求得：当

时，后验概率分布=p(x|Wn)取得最大值

于是，我们得到了两个新的随机变量和，其中被称为：基于一组可观测的随机变量W 1,W 2,W 3,···,Wn的最大后验估计。相应的=p(|Wn)为后验概率密度的极值。新生成的随机变量也具有链式的概率图结构，如图15.6(b)所示。

最大后验估计所形成的随机过程(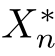)n≥0可以作为进一步优化控制的依据。例如，根据()n≥0来定义停止时间。