如何证明随机变量条件期望的近乎确定性？

习题14.1这里，我们将考虑：两个随机变量的和的均值和方差。

(a)证明：对于两个独立的随机变量x1和x2，它们的和x1+x2的均值µ等于：这两个随机变量（各自的）均值（分别为µ1与µ2）的和。也就是说µ=µ1+µ2。

(b)证明：对于两个独立的随机变量x1与x2，它们的和x1+x2的方差σ2等于：这两个随机变量（各自的）方差（分别为）的和。也就是说σ2=。

习题14.2假设一个随机变量的概率密度分布为：

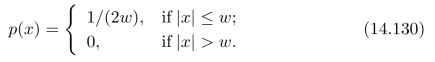
并且，我们独立地随机抽取出两个值，那么，这两个值的平均数的概率分布是什么？

习题14.3让我们来考虑Gauss分布和Poisson分布的一些性质。

(a)证明：Gauss分布

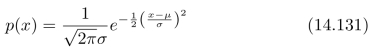
的均值和方差分别为：µ和σ2。

(b)证明：Poisson分布

的均值和方差都为m。

习题14.4考虑多个独立随机变量的加权平均和：

其中，xi的均值为m、标准差为σ。权重系数wi非负，并且，所有权重系数的和为1。求：y的均值和标准差。对于固定的N，求：使得y的方差取得最小值的系数wi。

习题14.5假设随机变量X∈Lp，也就是说，E(|X|p)＜∞，其中1≤p＜∞。请证明：对于任意λ≥0，都有：

这个结论称为Chebyshev不等式。进一步，我们得到了一个关于概率P的尾部估计：当λ→∞时，

习题14.6函数f的定义域为区间I∈R，如果对于任意x,y∈I以及t∈[0,1]，都有：

那么，我们称映射f:I→R为一个凸函数。请证明：对于任意的凸函数f，都有

其中X为在区间I∈R中取值的随机变量。这个结论称为Jensen不等式。进一步，请证明如下两个结论：

1.如果随机过程(Xn)n≥0构成一个鞅，那么，随机过程(|Xn|)n≥0构成一个子鞅。

2.如果随机过程(Xn)n≥0构成一个鞅，那么，随机过程(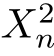)n≥0构成一个子鞅。

习题14.7假设随机变量X,Y∈L1，也就是说，E(|X|)≤∞和E(|Y|)≤∞。请证明：对于任意的σ-代数G，都有

几乎确定成立。

习题14.8假设X是一个非负的随机变量，Y=E(XG)是Xσ-代数G下的条件期望，请证明：

几乎确定成立，也就是说，

几乎确定成立。

习题14.9假设随机变量X,Y∈L2，也就是说，E(|X|2)≤∞和E(|Y|2)≤∞。如果

几乎确定成立，请证明X=Y几乎确定成立。进一步，请证明这个结论对于X,Y∈L1的情况也成立。

提示：首先通过习题14.6中的Jensen不等式分析L1空间与L2空间之间的相互关系。

习题14.10假设随机过程(X n)n≥0中各个随机变量Xn只从由k个实数组成的集合E={x1,x2,···,xk}中进行取值。请证明如下结论：(www.xing528.com)

•随机过程(Xn)n≥0构成鞅的充分必要条件为：对于所有的n和所有的xi0,xi1,···,xin∈E，都有

习题14.11假设随机变量X 1,X 2,···之间相互独立，并且满足：

其中pn,qn＞0，并且pn+qn=1。令Sn=X 1+X 2+,···,+Xn，请证明：随机过程(Sn)n≥1构成鞅。进一步，请证明：当pn=1/n2时，随机过程(Sn/n)n≥1几乎确定收敛，也就是说，当n→∞时，Sn/n收敛几乎确定成立。

习题14.12对于随机过程(Xn)n≥0，定义：

请证明：如果(Xn)n≥0是一个鞅^[22]，那么对于任意λ≥0，都有

这个结论称为Doob极大值不等式，在鞅理论中起到了奠基石作用。

习题14.13请进一步完善图14.7中的实验，完成研究报告。

(a)分别选取频率域中8×8、16×16、32×32和64×64的中心区域进行随机采样，舍弃概率分别选为0.3、0.5、0.7和0.8。通过观察和对比所得到的纹理图像，你能发现什么规律？

(b)选取频率域中更多方向的直线，例如30°、60°、120°和150°的方向，进行固定采样，通过观察和对比所得到的纹理图像，你能发现什么规律？固定采样的实现方式参见第7章习题7.10。

(c)在频率域中上述方向的直线上进行随机采样，舍弃概率分别选为0.4、0.5、0.6、0.7和0.8。通过观察和对比所得到的纹理图像，你能发现什么规律？

提示：为了便于开展对本题的研究，我们在此附上了图14.7所对应的MATLAB程序，如下所示：

【注释】

[1]注意，每一个子集对应于一个n位的二进制码，具体规则如下：如果ωk属于该子集，那么这个二进制码的第k位取1，反之取0。这样的n位的二进制码的总个数为2n，因此，包含n个元素的集合的所有子集个数为2n。

[2]注意，F=σ(A 1,A 2,···,Am)中的元素个数最多为2n个（集合Ω所有子集的个数），而并非无穷多个，因此，集合运算σ(A 1,A 2,···,Am)最终一定会停下来。对于n→∞的情况，上述分析不再成立，我们将其留作思考题。

[3]首先，从B 1,B 2,···,B k中选取若干个（包括1个和k个）进行并运算，总共可以生成2k-1个集合，加上空集（即ϕ=B 0∪B 0），总共有2k个集合。

[4]注意：直接通过“基本单元”A 1,A 2,···,Am，需要至少两种集合运算（例如：并和补），才能生成F。现在，我们可以理解：在（对集合Ω的）分割中强行加入空集（即B 0=ϕ）的必要性，否则，只通过集合并运算无法生成F中的空集ϕ。

[5]注意，随机变量X是一个函数，而不是一个变量，因此，不存在诸如“当X=5时”或“令X=5”之类的说法，而应该是“X=5所对应的事件”。这是初学者常犯的一个的概念性错误（我也曾经犯过）。你可以尝试解释P(X=5)的含义，来判断你是否正确理解了随机变量。

[6]这里，带引号的随机变量（“随机变量”）表示：前面的随机变量（初步）中所定义的随机变量，在后续完善随机变量的定义后，我们将去掉引号。

[7]我们后面会给出可测函数的更加具体和严谨的定义，并说明这两种定义方式是一致的。

[8]注意：概率（函数）只能对（集合Ω的）σ-代数F中的元素（也是Ω的子集）进行映射。

[9]假设P(X-1(x))=a＞0，由于P(X-1(x))在x点连续，可以找到x点附近的一个小区间Δx，使得其中任意一点xi都满足P(X-1(xi))＞0.5a＞0。区间Δx中有无穷多个点，我们从中挑选出n个点，可以得到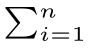 P(X-1(xi))＞0.5na，由于 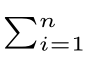P(X-1(xi))≤1，因此，0＜a＜2/n。令n→∞，则a→0。

[10]我们只需将“0.”换成“1.”或者“0.0”，即可将上述（二进制）数“放到”实数轴上的区间[0,2)或者[0,1/2)中去。点的个数始终保持不变，但区间长度却不相同。我们不对此做深入讨论，只是想强调：线段并不等价于无穷多个点排列在一起，因此，不能通过点来描述线段，而是要通过小区间描述线段。

[11]例如：k=1所对应于的一组（共n个）点与k=n-1所对应的一组（共n个）点中，一定有一组点的概率密度p(x)=∞；同理，k=2所对应的一组（共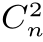=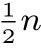(n-1)个）点与k=n-2所对应的一组（共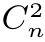=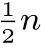(n-1)个）点中，一定有一组点的概率密度p(x)=∞；以此类推。

[12]注意，“积分就是算面积”这句话本身是没有错的。黎曼积分用来算“曲线下的面积”，而其他积分形式的设计，是为了克服“曲线”这两个字的约束。当然，除了著名的勒贝格积分外，还有多种不同的积分方式。这些积分往往只是形式表达而非具体计算公式，即使是对于黎曼积分，绝大多数函数也无法直接通过公式来计算。

[13]在二维离散Fou rier变换的结果中，中间的区域对应于高频分量，我们需要将低频分量“移到”中间，例如，可以调用MATLAB中的命令あtshift。

[14]事实上，牛顿在提出万有引力之后，花了近二十年的时间来创立微积分，一个很重要的需求就是：用一个点来“等效替代”一个球体。对于我们来说，用天体的重心来替代天体进行分析，似乎是很自然的，但是，在当时却是一个棘手的问题。

[15]参见本章14.5.2小节中的分析。

[16]“鞅”这个字的翻译并不好，其中文意思“古代用马拉车时套在马颈上的皮套子”是对英文m artingale的直译。事实上，m artingale所“隐喻”的意思是：今年投资，明年会不会后悔。也就是说，明年所得回报的期望值是否会高于今年的投资。

[17]我们再次强调，X n+1是关于“前n+1次”实验结果的随机变量，而不是关于“第n+1次”实验结果的随机变量。

[18]式(14.59)中第二项的一个更简单的理解方式是：Yn+1只取决于第n+1次实验，与前n次实验无关。从这个角度出发，我们不难理解为什么对于所有的

[19]事实上，这个问题困惑了我很长时间。通过数值计算实验，我猜测出了这个结果，但是，一直没能给出相应的证明。最终，南京大学数学系的张明敬老师给出了数学分析。

[20]式(14.109)对x求导，再令导数等于零，可以求得极值点为x*=k/n。

[21]注意，事件{T≤k}∈Fk，而事件{T＞k}是事件{T≤k}的补集，根据σ-代数的定义，事件{T＞k}∈F k。

[22]根据习题14.6，如果(X n)n≥0是一个鞅，那么(|X n|)n≥0是一个非负的子鞅。因此，这个结论对于非负子鞅也成立。