随机过程和鞅：理论与实践优化

我们不断地进行实验，到第n次实验时，所有可能的结果构成集合Ωn。根据集合Ωn，可以生成集合Ω的σ-代数为Fn，对应的随机变量（一个从Ω到实数轴R的可测函数映射）为：

所形成的一个随机变量序列：

被称为（离散时间的）随机过程。注意，“到第n次实验时”和“第n次实验”并不是一回事。例如，在“抛骰子赌大小”的例子中，“第n次实验”的结果有两个：“大”和“小”，而“到第n次实验时”的结果确有2n个：一个n位的“大”“小”序列。

14.7.1　随机过程的概率空间

集合Ω中的元素ω是：所有实验结果按顺序排列所组成的一个无穷长的序列^[15]：

其中ωik表示第k次实验的结果。元素ω有无穷多个。集合Ωn中的元素是：前n次实验结果按顺序排列所组成的一个长度为n的序列：

假设：在第k次实验中共有m k种可能的实验结果，那么，Ωn中（形如式(14.46)的）的元素个数为：m 1×m 2×···×mn。我们将前n次实验结果相同的情况全部归为一类，记为：

集合是Ω的子集，并且，所有的再加上空集ϕ就构成了：对集合Ω的一组分割，进而可以通过并运算生成（集合Ω的）σ-代数Fn。也就是说，根据集合Ωn，实现了对集合Ω的分割，从而生成集合Ω的σ-代数为Fn。随机变量X n是一个可测函数，必须将中的所有元素映射为同一个值！我们并不知道（式(14.47)所示的）集合中元素的具体信息，只知道集合中元素的前n位的信息：式(14.46)所示的集合Ωn中的元素。随机变量Xn通过：对Ωn中的元素的函数映射，来实现：对（集合Ω的一组分割中的）子集中所有元素的可测函数映射！具体地说，对集合中元素ω的映射结果Xn(ω∈)，是通过元素ω∈的前n位（即前n次实验结果ωi1,ωi2,···,ωin）计算出来的。

根据式(14.47)，在进行第n+1次实验后，集合将被进一步细分为多个子集{}，对应于不同的ωin+1，也就是说，

于是，所有的{}再加上空集ϕ就构成了：对集合Ω的一组更“精细”的分割，进而可以通过并运算生成（集合Ω的）更“精细”的σ-代数Fn+1，并且，Fn⊆Fn+1。也就是说，所有这些σ-代数之间形成了一种嵌套包含关系：

我们将其称为过滤子。（集合Ω的）σ-代数Fn描述了：到第n次实验时，我们所获取到的关于集合Ω的（一部分）信息。随着实验的不断进行，获取到的关于集合Ω的信息越来越多，因此，不难理解式(14.49)所描述的过滤子关系。

图14.10展示了“抛骰子赌大小”的例子。单次的实验结果包括两种情况：{ω1=大,ω2=小}。根据这两个结果，对于每一次实验，集合Ω都被相应地分成了两部分：

1.第k次实验结果为ω1（其他实验结果任意），记为：；

2.第k次实验结果为ω2（其他实验结果任意），记为：。

在图14.10中，我们用“双箭头线”标出了：（不同k的情况下）

图14.10　对于每一次实验，集合Ω都被相应地分成了两部分：(1)第k次实验结果为ω1（其他实验结果任意），记为：∈Ω；(2)第k次实验结果为ω2（其他实验结果任意），记为：∈Ω。根据（所有的）（k=1,2,3,···），可以计算出（所有n=1,2,3,···所对应的）对集合Ω的分割,m=1,2,···,2n，具体过程为：，也就是说，将区间一分为二，得到两个新的区间。所有新生成的区间就形成了：对集合Ω的一组“粒度”更细的分割。相应的σ-代数之间形成了一种嵌套包含关系：F 1⊆F 2⊆F 3···，称为过滤子。随机变量X n要将集合Ω的分割,(m=1,2,···,2n)中的每一个小区域中的所有元素都映射成同一个值。因此，X 1（的映射结果）中包含2个点，X 2中包含22=4个点，X 3中包含23=8个点，以此类推。

所对应的集合Ω中的区域。没有用“双箭头线”标出的区域对应于：（不同k的情况下所对应的）。子集和可以包含Ω中的多个不连通区域。我们用{},m=1,2,···,2n表示：（到第n次实验时）σ代数Fn所对应的（对Ω的一组）分割中的所有非空集合。

根据（所有的）（k=1,2,3,···），通过如下过程：

1.初始值：。

2.当k≥1时，计算：

也就是说，将区间一分为二，得到两个新的区间和，即：。

3.所有新生成的（其中m=1,2,···,2k+1）就形成了：到第k+1次实验时，对集合Ω的一组“粒度”最细的分割。

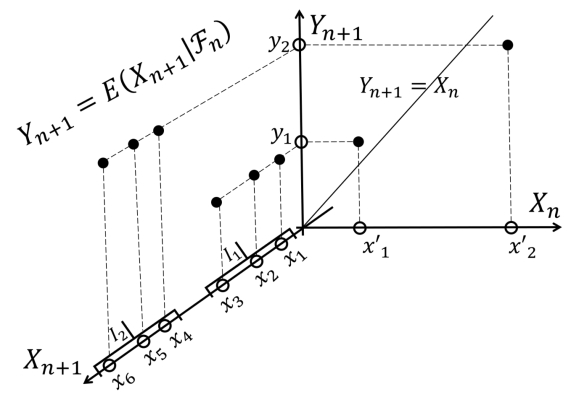
图14.11　为了分析第n+1次操作的效果，我们需要比较X n和X n+1。由于X n={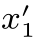,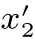}和X n+1={x1,x2,···,x6}中包含的点的个数不一致，首先要对X n+1中包含的点进行“合理的归并”，计算出X n+1条件期望Yn+1=E(X n+1|Fn)；然后，再对Yn+1={y1,y2}和X n={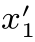,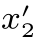}进行比较。由于y1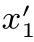＞而y2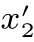＜，因此，随机过程(X n)n≥0既不是鞅，也不是超鞅，也不是子鞅。

可以逐步计算出：（所有n=1,2,3,···所对应的）对集合Ω的分割,(m=1,2,···,2n)，如图14.10所示。随机变量Xn要将：集合Ω的分割,(m=1,2,···,2n)中的每一个小区域中的所有元素，都映射成同一个值。因此，X 1（的映射结果）中包含2个点，X 2中包含22=4个点，X 3中包含23=8个点，以此类推。

14.7.2　鞅、超鞅、子鞅

对于随机过程，我们所关心的一个问题是：“情况”在如何变化？进而确定是否应该将过程继续进行下去。要回答这一问题，我们需要对X n和Xn+1进行比较。注意，X n和Xn+1中包含的点（或区间）的个数都不一致，要对其进行比较，首先要想办法将相应的点（或区间）的个数“变得”一致，参见图14.11。

注意，Fn⊆Fn+1，因此，X n+1中包含的点（或区间）的个数多于Xn中包含的点（或区间）的个数，我们需要对Xn+1中包含的点（或区间）进行“合理的归并”。“归并”过程要依据Fn，以确保归并后的点（或区间）的个数与X n中包含的点（或区间）的个数一致。“合理”是指：归并后的结果能够等效地“替代”Xn+1。上一小节中所介绍的条件期望：

正好可以用来完成这一任务。于是，我们可以通过比较X n和Yn+1，来对第n+1次操作做出评价。如果Yn+1≥X n，说明第n+1次的操作带来了利益；相反，如果Yn+1≤Xn，说明第n+1次的操作造成了损失。当然，还存在其他的情况：Yn+1≥X n只对于某些点（或区间）成立，对于其他的点（或区间），则是Yn+1≤Xn，如图14.11所示。

鞅是一种特殊的随机过程，对于所有的n≥0，都有

几乎确定成立。也就是说，每一次的操作（从统计意义上）既不带来额外的利益，也不造成损失^[16]。进一步，我们可以定义超鞅和子鞅：超鞅：对于所有的n≥0，都有E(Xn+1|Fn)≤X n几乎确定成立。子鞅：对于所有的n≥0，都有E(Xn+1|Fn)≥X n几乎确定成立。如果第n+1次操作什么都不做，那么^[17]，Xn+1=Xn。通过进行第n+1次操作，使得Xn+1变成一个新的随机变量，我们会不会后悔？鞅所描述的是一种“边界”情况，超过这个边界（超鞅），这些操作（在统计意义上）不断造成损失；在这个边界以内（子鞅），这些操作（在统计意义上）不断带来利益。当然，正如我们上面所指出的：鞅、超鞅和子鞅只是三种极其特殊的情况。随机过程(Xn)n≥0也可能既不是鞅，也不是超鞅，也不是子鞅，如图14.11所示。

14.7.3　两个具体例子

最后，我们通过两个例子，来深入理解上述内容。第一个是“抛骰子赌大小”的过程，单次实验有两种可能的结果：{ω1=大,ω2=小}。相应的概率分为：P({ω1})=a和P({ω1})=1a，其中0＜a＜1。对于第k次实验，定义随机变量：

其中∈Ω是由所有第k次实验结果为ω1（其他实验结果任意）元素所构成的集合，∈Ω是由所有第k次实验结果为ω2（其他实验结果任意）元素所构成的集合，参见图14.10。对于所有的k=1,2,3,···，都有：

令初始值X 0=0，当n≥1时，定义随机变量：

即：前n次实验的总“收益”。于是，X n和Xn+1之间的关系为：

进而，可以得到^[18]：m=1,2,3,···,2n，都有E(Yn+1|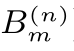)=E(Yn+1)。

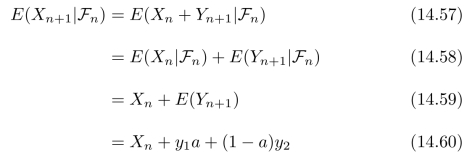
式(14.58)称为条件期望的线性性质。式(14.59)中的第一项参见式(14.37)，第二项参见图14.10和定义式(14.35)。

对于σ-代数Fn所对应的（对集合Ω的）一组分割{Fn}中的每一个非空区间（其中m=1,2,3,···,2n），随机变量Yn+1的加权平均值都是：

其中m=1,2,3,···,2n，因此，

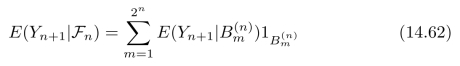
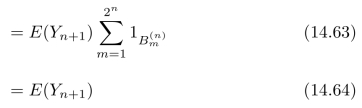
根据式(14.60)，可以得出如下结论：

1.当y1 a+(1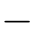a)y2=0时，随机过程(X n)n≥0是一个鞅。

2.当y1 a+(1a)y2≤0时，随机过程(X n)n≥0是一个超鞅。

3.当y1 a+(1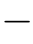a)y2≥0时，随机过程(X n)n≥0是一个子鞅。

第二个例子称为P´olya罐子，是很多现实问题的数学模型。在刚开始的时候，罐子里面有一个黑球和一个白球，我们不断地从罐子随机地抓球。如果抓到白球，就往罐子里面放回两个白球；同样地，如果抓到黑球，就往罐子里面放回两个黑球。在进行n次操作以后，罐子里面总共有n+2个球，我们用Wn表示：抓到白球的次数，那么，此时罐子里面总共有Wn+1个白球。我们定义随机变量：

也就是说，n次操作以后罐子中白球所占的比例。随机过程(Xn)n≥0构成一个鞅。事实上，P´olya罐子和“抛骰子赌大小”非常相似，“抓到白球”类比于“大”，“抓到黑球”类比于“小”。两个例子之间的不同在于：“抛骰子赌大小”过程中，每次实验都是独立的，出现“小”和“大”的概率是固定的，与第几次实验无关，但是，在P´olya罐子的例子中，“抓到白球”和“抓到黑球”的概率依据是：罐子里面（现有的）白球和黑球之间的比例，也就是说，第n+1次实验依赖于前n次实验的结果。

对于P´olya罐子的例子，集合Ω和过滤子F1⊆F2⊆F3···与前面“抛骰子赌大小”例子中的定义是完全一致的，只是此时{ω1=抓到白球,ω2=抓到黑球}，因此，我们在此不再进行赘述。此外，第k次操作所对应的随机变量Yk也与式(14.53)一致，只是此时y1=1、y2=0，于是，式(14.53)可以进一步写为：

经过第n+1次操作后，罐子里白球的数目变为：

第n+1次操作抓到白球的概率等于：罐子里白球的所占的比例Xn。因此，Yn+1在σ-代数Fn下的条件期望为：

根据定义，

于是，可以进一步计算得到：

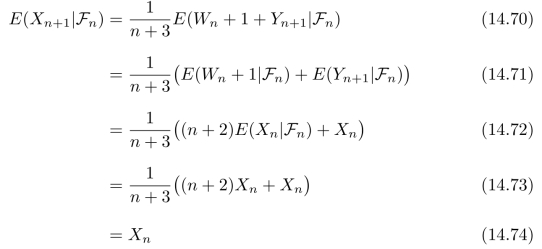
因此，随机过程(X n)n≥0构成一个鞅。进一步，我们可以计算：事件X n=(k+1)/(n+2)（或等价的Wn=k）的概率，结果为：

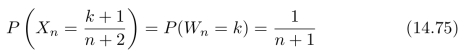
其中k=0,1,2,3,···,n。我们可以用数学归纳法来进行证明。当n=0时，式(14.75)成立。假设式(14.75)在n=m时成立，当n=m+1时，

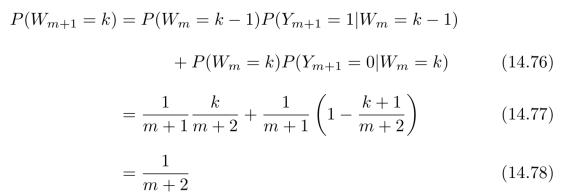
对于k=1,2,3,···,m都成立。当k=0时，

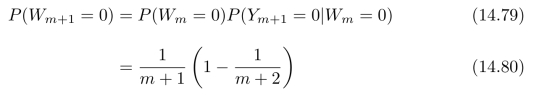
成立；当k=m+1时，

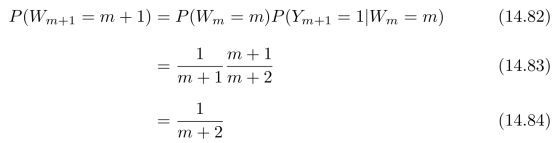
成立。因此，式(14.78)对于k=0,1,2,···,m+1都成立，证明完毕。

当n→∞时，随机过程(Xn)n≥0的极限X∞是什么？是不是实数轴上的连续区间[0,1]？答案是否定的！虽然Xn中的点都在实数轴上的连续区间[0,1]内，但是，Xn中的点具有“分数形式”k+1/(n+2)（其中k=0,1,2,···,n），也就是说，Xn中的点一定是有理数，而不可能是无理数！因此，当n→∞时，随机过程(Xn)n≥0的极限X∞是：实数轴上的连续区间[0,1)中的有理数集Q[0,1]，记为：

虽然有理数集Q[0,1]在区间[0,1]中并不连续（甚至其“长度”等于0），但是，我们仍然可以定义X∞的概率分布。事实上，Xn中所包含的n+1个点k+1/(n+2)（其中k=0,1,2,···,n）分布在：对区间[0,1]进行n+1等分所形成的一组（共n+1个）小区间

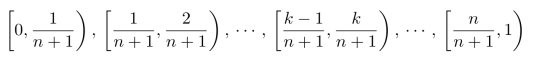
里面。不难验证：(www.xing528.com)

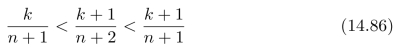
因此，每一个小区间里面只包含一个点。图14.12给出了n=9的情况，区间[0,1]被等分成10个小区间，X 9中所包含的10个点位于这10个小区间内，每个小区间内都有且仅有一个点。

与Xn相对应的（对区间[0,1]进行n+1等分所形成的）小区间Δx的长度为|Δx|=1/(n+1)，相应小区间所对应的概率为：小区间Δx中所包含的X n中的点（所对应事件）的概率，也就是说，

因此，对于所有的小区间Δx，其平均概率密度µ(Δx)/Δx都为1。令n→∞，此时Δx→0，于是，可以求得X∞的概率分布：

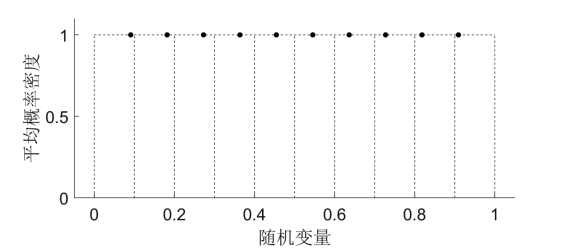
图14.12　随机变量X n中所包含的n+1个点k+1/(n+2)（其中k=0,1,2,···,n）分布在：对区间[0,1]进行n+1等分所形成的一组（共n+1个）小区间里面。每一个小区间里面只包含一个点。对于所有的小区间Δx，其平均概率密度µ(Δx)/Δx都为1。随着n不断增大，区间被越分越细，X∞的概率分布p(x)=1对实数轴上[0,1]区间中的每一个点x∈[0,1]都有定义。

注意，p(x)对实数轴上[0,1]区间中的每一个点x∈[0,1]都有定义。因此，我们可以将X∞完备化为：一个实数轴上[0,1]区间的连续型随机变量X，对应的概率分布为：p(x)=1（对于所有x∈[0,1]）。那么，X∞与X之间是什么关系呢？完备化的过程中，在实数轴上[0,1]区间内添加了许多（无理数）点，对于这些点，不存在集合Ω中的元素与之相对应，也就是说，

因此，对于由新添加的（无理数）点所组成的区间，所对应事件的概率为零，也就是说，

对于剩下的[0,1]区间中的有理数点x∈Q[0,1]，随机变量X∞与X是一致的。我们将这种情况称为：X∞和X几乎确定相等，也就是说，

通过上述分析，我们可以深入理解：鞅的定义式(14.52)中的“几乎确定成立”。本章中，如果不做特殊说明，随机变量之间的“相等”或“成立”，都是指“几乎确定相等”或“几乎确定成立”。

根据前面的分析，在P´olya罐子这个随机过程中，鞅(X n)n≥0的极限“几乎确定”是：区间[0,1]上的服从均匀分布p(x)=1的随机变量X。进一步，我们可以计算：在一组给定实验结果W 1,W 2,···,Wn,···条件下，X的一组条件概率分布p(x|Wn)（其中n=0,1,2,···）。

我们“铸造”一个骰子，使得其结果为“大”（对应于“抓到白球”）的概率服从[0,1]之间的均匀分布。注意，这个骰子本身就是一个（服从[0,1]之间均匀分布的）随机变量X，而并非一个“实物”，我们不妨称其为“随机骰子”。在X=x∈[0,1]这个事件下，经过n次“抛骰子赌大小”后，结果为“大”（对应于“抓到白球”）的总数是一个随机变量Wn。

在事件X=x∈[0,1]的条件下，事件Wn=k的条件概率为：

其中k=0,1,2,···,n。式(14.92)也称为二项式分布：k次“大”的概率xk乘以n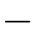k次“小”的概率(1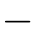x)n-k再乘以“出现这种情况的次数”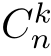，其中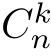，为：从“n个”中取“k”个的所有组合数目，即：

其中n!=n×(n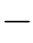1)×···×2×1表示n的阶乘。用“随机骰子”X进行n次实验后，事件Wn=k的条件概率也是一个随机变量：

事件Wn=k的概率是：这个随机变量的数学期望，也就是说，

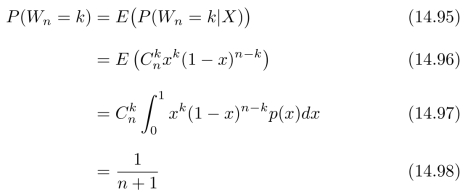
其中，p(x)=1。注意，上面这个（基于“随机骰子”X的）(Wn)n≥0的概率分布完全等同于在P´olya罐子实验中的(Wn)n≥0的概率分布，参见式(14.75)。因此，基于“随机骰子”X的实验和P´olya罐子实验是相同的随机过程。我们用基于“随机骰子”X的随机过程来等效替代基于P´olya罐子的随机过程，进而计算出：根据P´olya罐子实验结果W 1,W 2,···,Wn,···得出的关于X的条件概率分布。

在继续分析之前，我们有必要先解释一下式(14.97)的计算过程（其中p(x)=1）。事实上，式(14.97)是微积分中的一道有趣的习题^[19]。首先，令：

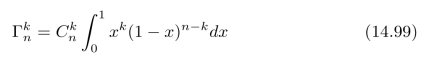
通过分部积分，可以进一步计算得到：

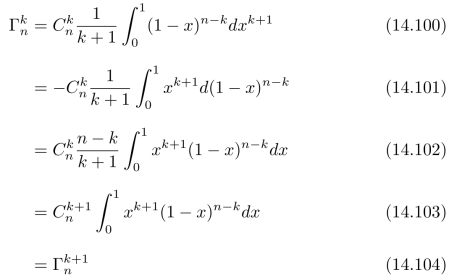
上式的一个直接结论是：，因此，对于所有的k=0,1,2,···,n，都有

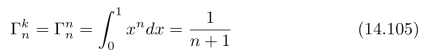
根据贝叶斯公式，可以进一步计算：在事件Wn=k的情况下，事件X=x的条件概率（称为后验概率），即：

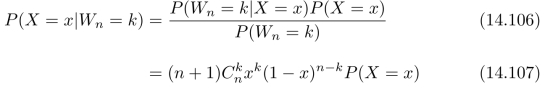
相应的概率密度分布：

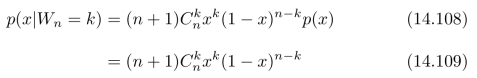
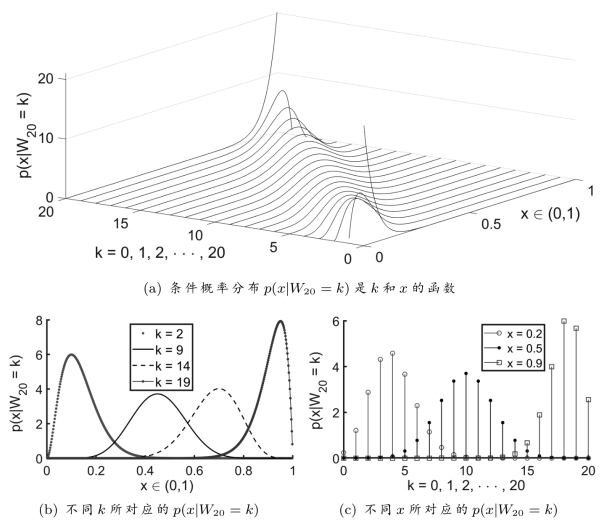
图14.13　当n=20时的条件概率分布。(a)函数p(x|W 20=k)的取值同时取决于k和x。(b)对于某一固定的k，条件概率分布在x=k/n处取得最大值。(c)当x固定时，p(x|W 20=k)是一个关于k的离散函数，在nx附近的整数k≈nx处取得最大值。

称为：在事件Wn=k的情况下，随机变量X的条件概率分布。图14.13给出了n=20所对应的条件概率分布p(x|W 20=k)。随机变量X的条件概率分布依赖于Wn的取值k，并且在x=k/n处取得最大值^[20]，参见图14.13(b)。当x固定时，p(x|W 20=k)是一个关于k的离散函数，在nx附近的整数k≈nx处取得最大值，参见图14.13(c)。

条件概率分布p(x|Wn)也是一个随机变量，记为：

相应的随机过程构成一个鞅。经过一步操作后，Wn+1有两种可能的结果：Wn+1或Wn，相应的概率为：

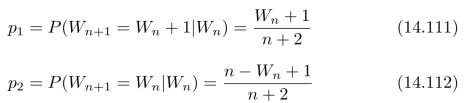
根据定义，随机变量

相应的条件期望为：在两种情况Wn+1=Wn+1和Wn+1=Wn下，的加权平均值，即：

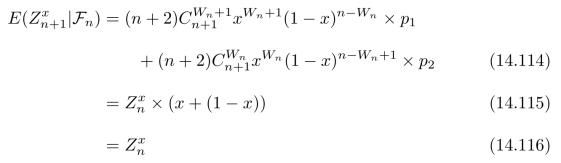
因此，随机过程是一个鞅。

前面谈到，“随机骰子”实验中的(Wn)n≥0和P´olya罐子实验中的(Wn)n≥0具有完全相同的概率分布，参见式(14.75)和(14.98)。之所以会出现这个“巧合”，其背后更深层次的原因是：随机过程(X n)n≥0构成一个鞅，因此，对于n=1,2,3,···,都有

而Xn和Wn之间存在一一对应的关系。

P´olya罐子实验之所以重要，是因为它是很多现实问题的数学抽象。例如：做好了一个项目同时带来了一个新的项目，干砸了一个项目同时失去了一个潜在的项目。在本章给出的P´olya罐子例子中，“奖励”和“惩罚”的力度是一样的，因此不难想象：罐子里面白球所占的比例X n的数学期望始终维持在1/2。通过提高“奖励”力度（例如放回3个白球）或降低“惩罚”力度（例如放回1个黑球），会使得X n的数学期望不断增加；相反，降低“奖励”力度（例如放回1个白球）或提高“惩罚”力度（例如放回3个黑球），会使得X n的数学期望不断减少。我们将相关分析留作练习题。

14.7.4　停止时间

对于一个随机过程，我们自然地想试图对其施加人为控制。一般情况下，我们无法控制（随机）过程中的规则，但是，能够决定是否应该停下来。于是，引出了一个重要概念停止时间：

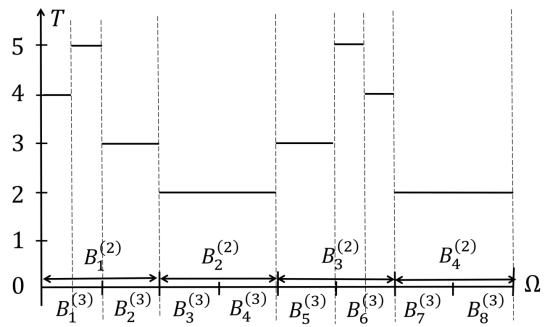
图14.14　停止时间是一个随机变量，其函数映射结果是整数。随机过程被执行步数所对应的控制条件，是通过Ω的“某个子集”（或区间）来定义的，也就是说，出现了具有“某些特征”的实验结果。到第n次实验时，我们只能根据实验结果“定位”一组小区间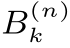（其中k=0,1,2,···），而无法继续“定位”小区间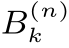中元素ω（参见14.7.1小节）。因此，第n步停下来的条件An={T=n}=T-1(n)一定是通过这些小区间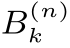描述出来，是这些小区间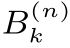的并集。

•停止时间：如果随机变量

满足：{T≤n}∈Fn对于所有的n≥0都成立，那么我们称T是一个停止时间。其中{T≤n}表示：T≤n所对应的事件，

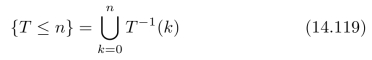
也就是说，{0,1,2,···,n}经过逆映射T-1所得到的Ω的子集。

停止时间是一个随机变量，其函数映射结果是整数，如图14.14所示。在本章14.7.1小节中，我们详细讨论了随机过程所对应的概率空间，到第n次实验时，我们只了解集合Ω的部分信息：Ωn。根据已获取信息Ωn，实现了对集合Ω的分割，从而生成（集合Ω的）σ-代数Fn。随着对集合Ω分割的不断细化，（集合Ω的）σ-代数之间形成了过滤关系：F0⊆F1⊆F2⊆···。

随机过程被执行步数所对应的控制条件，是通过Ω的“某个子集”（或区间）来定义的，也就是说，出现了具有“某些特征”的实验结果。随着实验的不断进行，集合Ω被划分得越来越细，到第n次实验时，我们只能根据实验结果“定位”一组小区间（其中k=0,1,2,···）中的某一个小区间，而无法继续“定位”小区间中元素ω（参见14.7.1小节）。因此，第n步停下来的条件An={T=n}=T-1(n)一定是通过这些小区间描述出来，是这些小区间的并集，也就是说，An∈Fn。事件

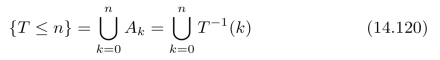
中的每一个Ak都属于Fn，因此，{T≤n}∈Fn。

综上所述，条件{T≤n}∈Fn是为了确保：对于所有在n步以内停下来的情况，仅根据前n次实验结果就能做出停止的决策。从应用的角度看，这一点是显然的，无需特别说明，但是，在数学上，只有明确了上述条件，才能将停止时间T和随机过程(X n)n≥0结合在一起。随机变量T和Xn不仅仅是关于Ω的函数映射，而且是可测函数映射，两者要结合，对应的σ-代数之间必须能够相容！

我们再次强调，停止时间T是一个随机变量，根据不同的实验结果取不同的值。容易验证：当T取固定值时（也就是说，对于所有ω∈Ω，都有T(ω)=N），T也是一个停止时间。此时，事件{T≤n}为：空集ϕ或全集Ω，都属于Fn。

对于一个给定的随机过程(Xn)n≥0，我们定义：

为一个受停止时间T控制的随机过程。

最后，我们通过一个定理来加深对上述概念的理论，并以此来结束本节内容。

•最优停止定理：

随机过程(X n)n≥0是一个超鞅，S和T是两个有界的停止时间，且S≤T，那么E(XT)≤E(XS)。

也就是说，对于超鞅，我们要“及时止损”。这符合我们的常识，通过证明过程，我们来检验是否真正理解和掌握了本小节的内容。要比较两者的大小，可以做减法，也可以做除法，通过除法比较大小需要预先知道其取值的正负，我们不知道这一点，所以做减法。注意，

上式是数学期望的线性性质。进一步，可以计算：

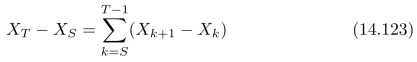
于是可以进一步得到：

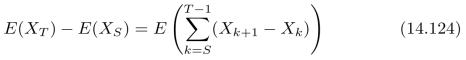
上式中的S和T是两个随机变量，而不是两个固定的数。因此，无法将式(14.124)中的求和符号直接提到括号外面。我们需要将式(14.124)中求和符号中的S和T换成两个固定的数，可以通过示性函数1S≤k＜T来实现，也就是说，

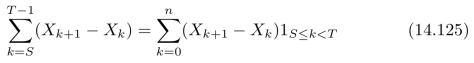
根据数学期望的线性性质，式(14.124)可以进一步写为：

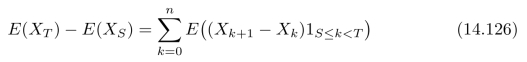
根据停止时间的定义^[21]，{S≤k}∈Fk，{T＞k}∈Fk。因此，事件{S≤k＜T}={S≤k}∩{T＞k}也属于Fk。由于(Xn)n≥0是一个超鞅，因此，E(X k+1|Fk)≤X k，也就是说，

因此，在任意一个区间{S≤k＜T}∈Fk上，都有

代入式(14.126)，最终完成了证明：

定理要求S和T是两个有界的停止时间，“有界”这两个字体现在式(14.126)中只有“有限项”进行求和。

通过这个定理的证明过程，我们想再次强调：停止时间是一个随机变量！在习题15.1中，我们通过一个应用实例“最优投资方案”，来研究如何通过设计停止时间进行随机优化控制。