条件期望的区间定义与示性函数相关

根据概率分布，可以进一步计算随机变量X的加权平均值：

称为随机变量X的数学期望。上式右边的积分被称为：p(x)的一阶矩。对于离散型随机变量，代入式(14.17)和(14.18)，可以计算得到：

数学期望可以为我们的决策提供一种定量的参考依据。

熟悉物理的朋友可能会发现：式(14.25)中的数学期望E(X)正好是X轴的重心。从某种意义上说^[14]，可以用点E(X)来“等效替代”X轴上所有的点。对于某些实际应用，这种处理方式可能太“粗糙”，一种提升的方式为：将X轴划分为一组不相交的区间{Ik}，对于每一个区间Ik，都用一个点来对其进行“等效替代”。对于某一个区间Ik，该选哪一个点来进行“等效替代”呢？我们自然想到：选用区间Ik内所有点的加权平均值，从而引出了条件期望这一重要概念。

14.6.1　条件概率

我们还有一些细节问题需要处理，概率密度p(x)给出了计算（式(14.25)中的）数学期望E(X)的一组权重，但是，p(x)却不能直接用来计算区间Ik内所有点的加权平均值，我们需要对其进行归一化处理！对于区间Ik，如果µ(Ik)/=0，归一化后的权重系数：

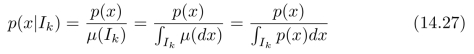
被称为条件概率密度。于是，我们可以计算区间Ik内所有点的加权平均值，即：

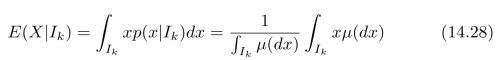
称为区间Ik的条件期望。如果µ(Ik)=0，则令E(X|Ik)=0。

注意，式(14.27)只针对x∈Ik（区间Ik内的点）有定义。通过定义示性函数：

可以有效地“规避”这个问题，

进而，我们可以将所有区间{Ik}的条件期望全部合在一起，形成一个关于x的函数y(x)，即：

注意，x=X(ω)是随机变量X（对集合Ω中的元素）ω的映射结果。因此，y是对（集合Ω中元素）ω的函数映射结果，也就是说，

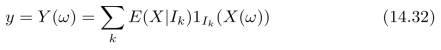
令Ak=X-1(Ik)，则式(14.32)可以进一步写为：

对于任意的k/=l，都有Ak∩Al=ϕ，并且，∪k Ak=Ω。因此，所有非空的Ak加上空集ϕ所组成的集合，就构成了对集合Ω的一组分割，记为{B l},(l=0,1,2,···)，其中B0=ϕ。（集合Ω的）分割{Bl}通过并运算，生成了集合Ω的一组σ-代数G=σ({Bl})，并且，G⊆F。

由于1φ(ω)=0且E(X|ϕ)=0，式(14.33)可以进一步写为：

我们将式(14.34)中的函数映射Y:Ω→R称为：基于（集合Ω的）分割{Bl},(l=0,1,2,···)的条件期望，简称条件期望，记为：

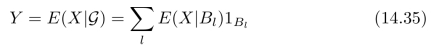
由于随机变量X是可测函数，因此，Bl∈F。根据式(14.34)，函数Y(ω)的逆映射结果Y-1(y)为：空集ϕ或B l或多个B l的并集，也就是说，Y-1(y)∈F，因此，映射Y:Ω→R是一个可测函数。也就是说，

•条件期望Y=E(X|G)是一个随机变量！(www.xing528.com)

图14.8给出了上面的分析过程。根据X轴上一组不相交的区间I1,I2,I3,I4，通过逆映射X-1可以找到：（集合Ω的）一组分割中的非空子集B1,B2,B3,B4。每一个集合Bk中的所有元素ω∈Bk都被映射为同一个数y=yk。我们令yk=E(X|Ik)，即X轴上区间I1的加权平均值。于是，对于任意ω∈Ω，我们通过ω→x→y的方式定义了一个新的函数映射Y:Ω→R，称为条件期望。

当然，X轴上的某些区间（例如图14.8中的I5）并没有ω与之相对应，也就是说，µ(I5)=P(ϕ)=0，因此，E(X|I5)=0。根据式(14.31)，我们可以直接忽略这样的区间。

14.6.2　复合函数映射

我们在上一节中谈到，通过随机变量和概率将概率空间中的(Ω,F)映射到二维实数空间XP平面（参见式(14.12)），从而赋予概率空间数的结构，以进行定量分析。事实上，条件期望就是一个很好的例子。条件期望所实现的函数映射y=Y(ω)包括两个过程x=X(ω)和y=y(x)（式(14.31)），即：

条件期望是这两个过程（x=X(ω)和y=y(x)）的复合函数形式，即：Y(ω)=y(X(ω))。“过程2”是在XP空间中进行的，计算过程中用到了条件概率，来对随机变量在区间内的取值做加权平均。

我们来做一下总结，集合Ω的σ-代数F对应于一组（集合Ω的）分割{Ak},(k=0,1,2,···)，我们将其中的某些Ak合并在一起，形成一组“粒度”更大的对（集合Ω的）分割{Bl},(l=0,1,2,···)。这组分割生成了集合Ω的另一个σ-代数G=σ({B l})。显然，G⊆F。随机变量X将集合Ak中的元素ω∈Ak映射成同一个实数xk（可测函数的定义）。随机变量Y应该将集合Bl中的元素ω∈B l映射成什么？集合B l=∪m Am（可能）是多个Am的并集，这组{Am}被随机变量X映射为一组数{xm}，条件期望Y=E(X|G)将集合Bl中的元素ω∈B l映射成{xm}的加权平均值：

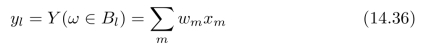
权重系数wm=P(Am)/P(Bl)为：事件Bl发生的情况下，事件Am的条件概率。总结如下：

•条件期望是在不同“粒度”的σ-代数G情况下的随机变量（即一个可测函数映射），其中，G⊆F。

图14.8　根据X轴上一组不相交的区间I1,I2,I3,I4，通过逆映射X-1找到：（集合Ω的）一组分割中的非空子集B 1,B 2,B 3,B 4。每一个集合Bk中的所有元素ω∈Bk都被映射为同一个数yk=E(X|Ik)，即X轴上区间I1的加权平均值。上述方式所定义的函数映射Y:Ω→R被称为条件期望。区间I1的逆映射结果为空集ϕ，也就是说，µ(I5)=P(ϕ)=0，因此，E(X|I5)=0，我们可以直接将其“忽略”。

具体地说，我们对随机变量X的取值进行归并，然后，通过逆映射X-1找到：归并在一起的各个xm所对应的（集合Ω的）子集Am，进而，以各个Am的条件概率作为权重系数，计算各个xm的条件期望（加权平均值），来取代归并在一起的这些{xm}，从而实现了复合函数映射Y(ω)=E(X(ω)|G)。显然，对于最细“粒度”G=F的情况，

对于最粗“粒度”G={ϕ,Ω}的情况，

另外一个显然的结果是：

这是一个不需要证明的结论，既然通过条件期望所选取的点能够“替代”相应的区间，那么对这些点求加权平均，自然等价于对这些区间（即整个X轴）求加权平均。

图14.9　一个具体的例子：“抛骰子赌大小”。(a)集合Ω={ω1,ω2,ω3,ω4,ω5,ω6}共有6个元素，随机变量X将其映射为实数轴（X轴）上的6个点。(b)将实验结果分为：B 1={ω1,ω2,ω3}和B 2={ω4,ω5,ω6}，条件期望Y=E(X|G)是一个随机变量，将B 1中的三个元素ω1、ω2、ω3映射为一个值y1=E(X|B 1)，将B 2中的三个元素ω4、ω5、ω6映射为另一个值y2=E(X|B 2)。

最后，我们来看一个具体的例子：“抛骰子赌大小”，如图14.9所示。集合Ω={ω1,ω2,ω3,ω4,ω5,ω6}，其中ω1=1点，ω2=2点，ω3=3点，ω4=4点，ω5=5点，ω6=6点。随机变量X将其映射为实数轴上的六个点xi=X(ωi)，其中i=1,2,···,6，如图14.9(a)所示。集合Ω的分割中的非空集合：{ω1},{ω2},{ω3},{ω4},{ω5},{ω6}，对应的概率为：Pi=P({ωi})，其中i=1,2,···,6。集合Ω的σ-代数F为：由集合Ω的64个子集所组成的集族。

如果我们将实验结果分为“小”和“大”两类：B1={ω1,ω2,ω3}和B2={ω4,ω5,ω6}，此时，集合Ω的σ-代数G为：{ϕ,B1,B2,Ω}。此时，P(B1)=P1+P2+P3，P(B2)=P4+P5+P6。进一步，可以求得：

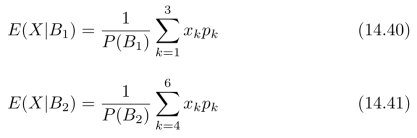
在σ-代数G下的条件期望为：

此时，yi=Y(ωj∈Bi)，也就是说，随机变量Y将B1中的三个元素ω1、ω2、ω3映射为一个值y1=E(X|B1)，将B2中的三个元素ω4、ω5、ω6映射为另一个值y2=E(X|B2)，如图14.9(b)所示。

条件期望Y=E(X|G)是一个随机变量，其定义域Ω也是随机变量X的定义域，我们可以尝试去比较这两个随机变量X和Y，例如：将图14.9(a)和14.9(b)“叠加”在一起，来探索从X到Y到底是“变好”了还是“变坏”了。由此引出了一个重要概念鞅，我们将在下一节中对其进行详细讨论。