概率分布的定义和性质

现在，我们可以直接在XP平面上进行分析，集合Ω中的元素ωi被映射成了二维空间中的点(X(ωi),P(X-1(X(ωi))))。正如我们前面所指出的：图14.4中的抽象集合Ω不是数轴，加上“虚线”只是为了美观。一般情况下，我们不将图14.4中的Ω空间画出来，而是将其记在心中。对于图14.4中X轴上的（除了X(Ω)以外的）其他点，X的逆映射将它们映射为空集ϕ，因此，这些点都对应于P轴上的零点。也就是说，对于X轴上的任意一点x∈R，都有（且仅有）P轴上的一个点P(X-1(x))∈[0,1]与之相对应！因此，我们不再关心x轴上的点是否有集合Ω中的元素与之相对应，函数P(X-1(x))的定义域是整个X轴（而不是X(Ω)）。

14.5.1　概率密度函数

当函数P(X-1(x))在某一区间Δx连续时，如果某一点x∈δ的值大于零，那么这一点的值一定无限接近于零^[9]。对于这种情况，很难直接分析P(X-1(x))，于是，我们自然想到去分析函数P(X-1(x))的“导数”。需要指出的是：P(X-1(x))并不是一个复合函数，因为X-1(x)是一个“一对多”的映射，而并非一个函数。因此，无法直接通过复合函数求导的方式来对函数P(X-1(x))“求导”。为了解决这个问题，我们首先需要探讨P(X∈Δx)的含义。对于区间Δx中的任意一点x，都可以通过逆映射X-1(xi)找到其对应的Ai∈F，于是，整个区间Δx的逆映射结果就是：所有这些Ai的并集，也就是说，X-1(Δx)=∪iAi；然后，我们再通过概率（一个集合测量函数）对其进行测量（其中xi∈Δx）：

所得到的结果就是P(X∈Δx)。我们可以通过P(X∈Δx)来定义（X轴上）区间Δx的测度（线段Δx的质量）µ(Δx)，即：

也就是说，（集合Ω中）被映射到区间Δx中（的元素所构成的）子集的概率，如图14.5(a)所示。

通过计算线段质量µ(Δx)与区间长度Δx之间的比值，可以得到区间Δx的（平均）密度；进一步，令Δx→0，所得到的极限：

被称为概率密度函数或概率分布。根据概率的定义，概率密度函数p(x)需满足两个重要性质：1)非负性，也就是说，p(x)≥0；2)归一性，也就是说，

最后，需要指出的是，对于离散型随机变量（X(Ω)对应于X轴上的一系列不连续的点），上面的分析方式仍然成立，只是对于某些区间，当区间长度Δx趋于零时，µ(Δx)=P(X-1(xi))不再趋于零，此时，式(14.15)的计算结果为：

其中Pi=P(X=xi)=P(X-1(xi))，而δ(xi)是位于x=xi处的单位冲击函数。函数δ(xi)满足如下三条性质：1)当x/=xi时，δ(xi)=0；2)当x=xi时，δ(xi)=+∞；3)对于任意函数f(x)，都有

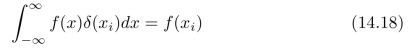
图14.5　(a)我们可以通过P(X∈Δx)来定义（X轴上）区间Δx的测度（线段Δx的质量）µ(Δx)。(b)将区间划分得越来越小，所得到的极限被称为概率分布。

事实上，概率分布给出了X轴的（归一化）密度分布！对于连续型随机变量，X轴上的点没有质量，可以通过区间的质量来计算（X轴上）点的密度；对于离散型随机变量，X轴上的（某些）点有质量，对应的密度为无穷大，需要借助单位冲击函数来对其进行表示。

14.5.2　两个具体例子

让我们来看两个具体的例子，以加深对相关概念的理解。首先，我们谈一下如何通过“抛骰子赌大小的方式”来实现图14.5所示的过程。抛一次骰子，会出现两个实验结果“大”和“小”。继续抛下去，所得到的实验结果是一串由“大”和“小”组成的序列，例如：

大大小小小大小小大······

在数学家的眼里，例如G.Cantor，这个序列“就是”一个二进制的数：令“大”对应1，小对应0，上面的那个实验结果对应于数：

110001001···

我们可以进一步将上面的（二进制）数“放到”实数轴上的区间[0,1]中去^[10]，只需要在这串数前面加上“0.”，即：

0.110001001···

其对应的十进制数为：

不断地抛骰子，永远不停下来，所得到的结果（一串无限长的“大”“小”序列）就和实数轴上区间[0,1]中的所有点形成了一一对应的关系，也就是说，X(Ω)=[0,1]。因此，X是一个连续型的随机变量。

在集合Ω中，前n次实验结果（即只关注“大”“小”序列中的前n个）不同的序列总共有2n个，分别被随机变量X映射成了：实数轴上[0,1]区间的2n个等分点，即：

(www.xing528.com)

对应的2n个（长度为2-n）的小区间为：

小区间Δx的逆映射结果X-1(Δx)为：一系列“大”“小”序列所组成的集合，这些“大”“小”序列的前n次实验结果对应于：区间Δx的左端点乘以2n后的n位二进制表示形式。例如，区间[2/2n,3/2n)的左端点2/2n乘以2n后的n位二进制表示形式为：

逆映射X-1(Δx)所得到的集合A=X-1(Δx)（Ω的子集）中的元素ω具有如下形式：

假设抛骰子结果为“大”的概率为0＜a＜1，结果为“小”的概率为1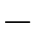a，那么，前n次实验结果出现上面所示的“小小···小小大小”（n个结果所组成的）序列的概率为：(1a)n-1 a1，这就是集合A=X-1(Δx)的概率P(A)。对于其他的小区间，我们都可以通过上述方法计算其概率，所有这些概率具体表现为如下形式：

其中k为（前n次）实验结果中出现“大”的次数。

当n→∞时，区间长度Δx→0，对应的概率µ(Δx)→0，我们可以进一步计算其比值（平均概率密度）：

图14.6(a)给出了a=0.51时的仿真结果，其中图14.6(a)是n=5时的25=32个小区间所对应的平均概率密度，图14.6(b)是n=20时的220=1048576个小区间所对应的平均概率密度。为了便于观察，图14.6(b)中并没有画出区间Δx，只画出了区间的左端点i/2n（其中i=0,1,2,···,2n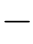1）。不难看出，概率密度函数p(x)并不是一个关于x的连续函数（尽管X是一个连续型随机变量）。连续型随机变量中的“连续”二字只是针对随机变量X而言的，与概率分布的性质无关。

通过这个例子，我们可以看到：（连续随机变量的）概率密度函数p(x)并不等同于我们脑海中的“一条连续曲线”。当我们用传统微积分的观点对其进行处理时，会碰到很多难以解决的问题。

当a/=1/2时，对式(14.22)取极限（令n→∞），某些点x的概率密度p(x)=∞，并且，这样的点有无穷多个^[11]。当然，这并不是说p(x)不存在，只是说明p(x)不存在“显式”的初等函数表达形式，而是通过极限形式表示出来的。遗憾的是我们难以通过计算机进行仿真，当n=30时，普通个人电脑已经很难进行计算和存储。

另一个重要的困难是：如何求p(x)（或含有p(x)）的积分？函数p(x)的点并不是“�在一起”的，没有形成曲线（参图14.6(b)），因此，难以通过（从计算曲线下面积的观点出发的）黎曼积分的方式，来求p(x)的积分。于是，出现了很多新的积分方式^[12]，对这些积分的深入讨论超出了本书的范围。

图14.6　当a=0.51时的仿真结果。(a)当n=5时，对应的25=32个小区间的平均概率密度。(b)当n=20时，对应的22 0=1048576个小区间的平均概率密度。

需要指出的是，我们通常将对函数f(x)的积分写为：

只有在（黎曼积分）可积的条件下，才将式(14.23)进一步写为：

式(14.23)是一个描述式：对f(x)的（所有）函数值做加权平均。无论式(14.24)中的黎曼积分能否顺利进行，式(14.23)始终是有定义的，因为可测函数X的定义保障了µ(Δx)=P(X-1(Δx))始终是可以计算的！

在第二个例子中，我们通过采样的方式，从噪声中生成纹理图像，如图14.7所示。为了便于显示，我们选择大小为128×128的噪声图像进行实验，如图14.7(a)所示。随机变量X服从区间[0,1]中的均匀分布，图14.7(a)对应于：随机变量X在实验过程中所生成的128×128个观测结果。统计直方图14.7(g)进一步验证了X服从均匀分布。

采样过程是在频率域中进行的。对随机噪声图像14.7(a)做二维离散Fou rier变换，图14.7(d)中给出了频率域中各个频率成分的幅值分布。然后，我们就可以对各个频率成分进行采样。我们通过两类不同的采样方式，得到了两种不同的中的纹理图案：

•随机采样：在频率域中的大小为32×32的低频区域进行随机采样^[13]，对于低频区域中的每一个频率分量，都以50%的概率进行舍弃。采样结果如图14.7(e)所示。

•固定采样：在频率域中，沿着经过中心位置的四条直线进行采样，其方向分别为：0°、45°、90°和135°，其中水平和竖直方向的“线宽”取为2，倾斜方向“线宽”取为3。采样结果如图14.7(f)所示。

图14.7(b)中给出了：通过随机采样方式所得到的纹理图像；图14.7(c)中给出了：通过固定采样方式所得到的纹理图像。我们可以轻易地看出：1)两张纹理图像14.7(b)和14.7(c)之间存在“明显”的不同，2)噪声图像14.7(a)与两张纹理图像之间存在“明显”的不同。如何将这三张图像中的“明显的不同”描述出来，却不是一件容易的事。我们可以尝试使用概率分布。对噪声图像14.7(a)和两张纹理图像14.7(b)和14.7(c)中的数据分别进行统计，可以得到三个统计直方图，参见图14.7(g)。为了便于观察，三张图像中的数据都被归一化到区间[0,1]。显然，图14.7(b)和14.7(c)中的数据不再服从均匀分布；此外，两个分布中心之间的距离足够大，约为0.55，分布之间的明显重合区域较小，不到0.2。因此，概率分布是一个有效的描述特征。

这个例子还告诉我们：图像中的某些纹理可能是噪声的滤波结果。这将使得某些机器视觉任务变得更加困难，因为我们可能会难以分辨哪些纹理是真实存在的（也就是说，由场景中的物体产生的）。

图14.7　通过在频率域的采样，从噪声中生成纹理图像。(a)。大小为128×128的随机噪声图像，每一个像素点的值都服从[0,1]均匀分布。(b)对随机噪声的频率域（离散Fou rier变换结果）中的低频区域（大小为32×32）进行随机采样，所得到的纹理图像。(c)对随机噪声的频率域沿着0°、45°、90°和135°方向的直线进行固定采样，所得到的纹理图像。(d)随机噪声图像(a)的离散Fou rier变换结果的幅值分布（中间位置对应低频区域）。(e)对频率域中大小为32×32的（中间部分的）低频区域进行随机采样，所得到的频域采样结果。(f)在频率域中，沿着0°、45°、90°和135°方向的直线进行采样（水平和竖直“线宽”取为2，倾斜“线宽”取为3），所得到的频域采样结果。(g)对噪声图像和两张纹理图像中的数据分别进行统计，得到的三个统计直方图。为了便于观察，三张图像中的数据都被归一化到区间[0,1]。