自动形成聚类的方法与应用

通常情况下，特征点会形成多个不同的聚类。我们可以通过自动的方法去发现：应该将哪些点结合在一起来形成聚类。这个过程被称为无监督学习。这类方法的工作原理是：不断地合并已有的聚类。一开始的时候，我们将每一个数据点看作一个独立的初始聚类；然后，在每一步的迭代过程中，我们找到：距离最小的两个聚类，并且，将这两个聚类合并为一个聚类；当聚类的种类等于我们所期望得到的数目时，或者，当聚类之间的最小距离大于某一阈值时，我们停止迭代。现在已经有许多启发式的方法用于指导这个迭代过程。

另外一个相反的方法是：将已有的聚类沿着某些合理的线分开。一开始的时候，所有的点被看作是一个大的聚类；在每一步迭代中，找到一个聚类将其分为两个聚类；当已经得到足够多的聚类种类，或者，如果继续分下去，不会使得某些我们提前设置的指标有很大提高时，我们停止迭代。但是，对于绝大多数我们感兴趣的情况，我们实际上是知道哪些点是属于同一类的。

事实上，分类的结果可以直接用于实现聚类。如果我们已经知道每一个类的中心，那么，我们可以根据：样本点到每一个中心点的距离，来确定样本点属于哪一类，这个过程已经实现了聚类；如果我们已经完成了聚类，那么，我们可以计算每一个类的中心。这是一个“鸡生蛋、蛋生鸡”的问题，因此，我们可以使用交叉迭代的方式进行求解，即著名的k-均值算法：

1.初始化：随机选取k个中心点（其中i=1,2,···,k），然后，对所有样本进行标注^[3]：

其中j=1,2,···,m为样本点的下标。最后，统计每一类样本点的数目：

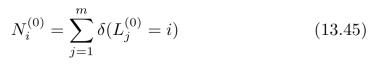
其中称为示性函数：当=i时，δ(=i)=1；否则，=0。

2.循环迭代：首先，根据第n次的标注结果，将k个中心点更新为：

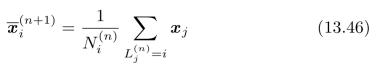
然后，根据更新后的中心点，对所有样本进行标注：

(www.xing528.com)

进一步，统计每一类样本点的数目：

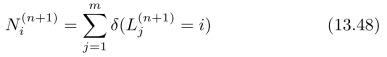
3.重复过程2，直到所有的中心点不再发生明显变化，也就是说，

对于所有的i=1,2,···,k都成立。

图13.7中给出了一个实验仿真结果，原始数据中共包含3个聚类，聚类的中心点分别为(3,0)、(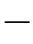3,0)和(0,3)。样本点服从σ=1的二维Gauss分布，如图13.7(a)所示。

随机选取三个样本点，作为三个聚类中心的初始估计结果，即图13.7(b)中的红色“方框”。然后，对每个样本点进行“归类”，结果如图13.7(b)所示。进一步，根据样本点的“归类”结果，更新相应的聚类中心，即图13.7(b)中的红色“圆点”。图13.7(b)中，更新前后的聚类中心估计结果发生了明显的变化，因此，继续进行迭代运算。在进行完4次迭代后，聚类中心估计结果不再随迭代更新而发生了明显变化，图13.7(c)中的红色“方框”与红色“圆点”几乎重合。

我们选择中心点来作为样本点的聚类中心，是因为中心点使得距离的平方和最小。对于所有第k类样本点x i，我们需要求解：

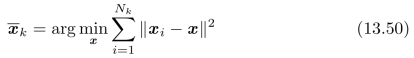
通过对求导，然后，令求导结果等于零，我们最后可以求得极值为：所有第k类样本点x i的平均值/Nk，也就是说，第k类样本{x i}的中心点。

注意，k-均值算法直接使用（和聚类中心之间的）最近距离，来对样本点进行归类。这一操作暗含的假设是：所有的类都服从Gauss分布，并且，各个类的标准差都相同。有兴趣的读者可以在此基础上针对更一般的情况继续进行分析和探索。