分类模型：最近邻分类和最近中心分类

分类模型的基本模式是：对被分类的物体进行n种测量；然后，将测量结果看作n维特征空间中的一个点。我们将探索使用各种算法，将特征空间划分为不同的区域。这些区域就是分类的依据，我们根据物体的特征向量落在哪个区域，来赋予物体相应的类别。被分类物体的每一种测量结果均被称为一个特征；将这n个特征测量结果“放在一起”，就构成了一个特征向量；特征向量所在的n维空间被称为特征空间。

这些和机器视觉又有什么关系呢？一旦图像被分割以后，我们可以对各个图像区域进行测量。然后，我们可以尝试通过：基于这些测量值的分类结果，来识别图像区域所对应的物体。一些简单的特征包括：二值图像区域的面积、周长、最小以及最大转动惯量。

对于这些方法，一个很重要的问题是：如何获取足够的信息，来智能地确定决策边界。如果我们可以得到“潜在的”概率分布，那么，我们可以通过：最小化某种误差标准，来确定边界的位置。尽管通常情况下，我们可以通过：从各个类采样出的有限个样本，来估计出相应的概率分布，但是，我们通常的做法是：直接利用这些信息，而不是估计概率密度。

这里，我们使用的一个基本假设是：属于同一个类的特征点会聚集在一起，而属于不同类的特征点会相互分离。有时，这个假设是不成立的，例如：模式分类方法无法很好地区分有理数和无理数，或者，（国际象棋的）棋盘上的黑色方块和白色方块。

在机器视觉的应用中，一个很严重的问题是：图像是三维实体的二维投影。因此，直接从图像中获得的简单的特征测量结果，会受到物体的空间姿态、光照以及距离等因素的影响。只有当模式分类方法是：基于那些不随成像条件的改变发生变化的特征时，才会取得好的结果。所谓“基于不随成像条件的改变而变化的特征”是指：我们能够通过图像得到对物体真实属性（例如：反射率和形状）的估计。当然，如果能做到这一点，我们的问题其实已经基本解决了。

13.3.1　最近邻分类

假设我们已经得到了从各个类中抽取出的样本。我们用x i,j表示：第i个类中的第j个特征向量。对向量x进行分类的一种方法是：找到和x最近的样本，然后，将x归于该样本所属的类。也就是说，对于某一k和l，如果下式：

对于任意的i和j都成立，那么，x被分为第k类，如图13.1(a)所示。

这种简单方法有两个问题。首先，各个类的样本通常会形成聚类。这些聚类之间可能有重叠的部分。如果某一个特征向量落在重叠部分中，那么，它会被分到：碰巧与它邻近的点所属的那一类。因此，在重叠区域内，分类基本上是随机的。这可能是这种方法能够取得的最好结果，但是，我们更希望能够得到一个简单边界。

一个改进的方法是：使用多个邻近点。例如，我们可以统计：在特征向量周围的k个近邻点中，哪一类的点的数目最多。这种方法在重叠区域会得到更好的分类效果，因为，这种方法提供了：对重叠区域中哪一个类的概率密度最大的估计结果。

最近邻分类方法的第二个问题出现在计算上。如果给定很多样本，我们需要很大的存储量。此外，除非我们事先找到某种方法来划分特征空间，否则，我们需要计算：要被分类的特征向量和所有样本之间的距离。最近邻分类方法是一种直接的计算方法，它不需要对各个类的分布有太多的假设。

在某些情况下，不同的聚类会形成：彼此之间没有重叠的区域。如果聚类的凸包没有交集，那么，用凸包所形成的区域来代替聚类中的所有样本点，可以节省计算量和存储空间。

最近邻分类方法的一个很大的优点是：聚类可以有很复杂的形状。聚类的形状可以不必是旋转对称的，甚至不必是凸的。

13.3.2　最近中心分类

现在假设：每一个类的样本都形成一个很好的椭圆形聚类，不同类型的聚类区域的形状很相似，并且，聚类之间彼此没有太多的重叠。在这种情况下，保存每一个类中所有的样本点就显得太浪费了。我们可以使用每个类的中心来表示该类。对于一个要被分类的特征向量，我们将其归为：中心距离它最近的那一类，如图13.1(b)所示。

这种方法大大地节省了计算量和存储空间。此外，类和类之间也通过光滑边界划分开来了。事实上，每一个类所对应的空间区域是：由超平面分割出来的凸多面体。凸多面体是凸多边形在三维及三维以上空间中的推广，它们是由超平面相交而形成的。为了说明类所对应的空间区域的边界是超平面，假设点x位于：聚类中心分别为的类所对应的空间区域的边界上，那么：

上式中，等号两边同时取平方，我们可以得到：

我们可以将上式进一步写为：

将上式展开，我们可以得到：

对上式做进一步整理，我们可以得到：

图13.1　最近邻分类和最近中心分类。(a)对向量x进行分类的一种方法是：找到和x最近的样本，然后，将x归于该样本所属的类。(b)我们可以使用每个类的中心来表示该类。对于一个要被分类的特征向量，我们将其归为中心距离它最近的那一类。

这是一个关于x的线性方程。它描述了一个法向量为并且经过点/2的平面。注意：曲面的法向量从一个聚类中心指向另一个聚类中心；而点/2正好是：两个聚类中心和的中点。因此，这个边界是连接两个聚类中心的线段的垂直平分面，如图13.1(b)所示。

如果聚类是旋转对称的，并且其区域形状相似，或者这些聚类在空间中是彼此分离的，那么，这种简单的空间划分方法是合适的。

13.3.3　概率分布模型(www.xing528.com)

如果两个邻近的聚类中，其中一个聚类的区域比另一个小，那么，我们应该将它们的边界移向（区域）较小的那个聚类的中心。类似的，如果聚类沿着某个方向（除了连接两个聚类中心的方向以外）被拉长，那么，边界应该朝着被拉长的方向偏转。实现上述边界调节过程的最好方法是：使用概率分布模型。

一般情况下，我们常常使用n维Gauss分布：

其中，表示均值，σ表示标准差。我们常常使用n维Gauss分布，不但因为它和实际应用中的概率分布很接近，而且因为其在数学上也易于处理。我们首先考虑：两个具有相同分散度（即：标准差σ）并且中心分别为的n维Gauss分布。我们可以将它们的边界设为：使得这两个概率密度取得相同值的地方，也就是说，

或者，更简单地说：

这里，我们又得到了一个关于连接两个聚类中心点的线段的垂直平分面的方程。我们找到了一个理论模型，用以证明：我们在前面通过探索式推理所引入的方法的正确性。这样设置边界位置，可以使得：两种不同类型的误差取得相同的值。

13.3.4　特征空间的划分

现在，我们假设：一个类比另一个类更常见。使用（连接两个聚类中心的线段的）垂直平分面作为边界，会导致相同的相对误差。也就是说，每一个类中都有相同比例的成员可能被错分。这可能是（也可能不是）我们想要的结果。显然，如果将边界移向：不常见的那一类的中心，那么，我们可以减小总误差。这是因为：这个调节过程虽然增加了罕见错误的发生概率，但是，减小了常见错误的发生概率。我们分别用p1和p2来表示：某一个要被分类的量分别属于第一类和第二类的概率，我们希望：

注意：p1和p2与特征测量结果无关！p1和p2两个量实际反映的是：对应的两个类中，哪一个类更加常见！也就是说，它们是人为赋予的一种“先验假设”。

通过对上式取对数，我们可以进一步得到：

也就是说，

这里，我们又一次得到了一个法向量为的超平面，但是，该超平面所经过的点（即：式(13.12)的解）为^[1]：

也就是说，超平面从的中点/2开始，沿着法向量方向平移了一段距离。超平面的平移方向为：指向概率p1和p2中的较小值所对应的聚类中心；平移量的大小为：

注意：如果σ足够大，并且，p2和p1的比例也足够大，那么，超平面的移动量可能会超出：连接两个聚类中心的线段的长度范围。

下一步，我们考虑一个聚类比另一个聚类更“紧凑”的情况。边界应该更靠近“更紧凑”的聚类的中心。假设两个n维Gauss分布的标准差分别为σ1和σ2。如果我们要求：在两个聚类的边界上，两个n维Gauss分布的概率密度的大小相同，那么，我们可以得到：

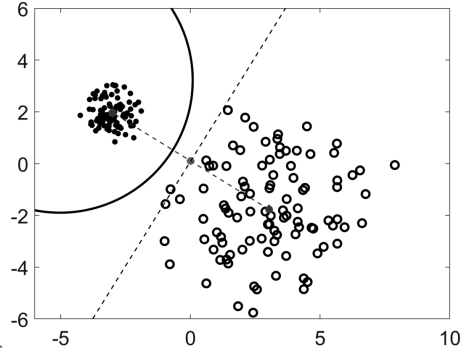
图13.2　如果一个聚类比另一个聚类更“紧凑”，那么，边界应该更靠近“更紧凑”的聚类的中心。此时，边界曲面不再是一个超平面（图中的黑色虚线），而是一个抛物面（图中的黑色曲线）。

对上式中的等号两边取对数，我们可以进一步得到：

在上式的进一步整理结果中，我们无法消掉x T x，因此，边界曲面不再是一个超平面，而是一个抛物面，如图13.2所示。

尽管我们无法“看见”高维抛物面，但是，仍然可以通过式(13.16)来进行决策。我们可以将上述方法和结果推广到多个类的情况。概率密度相等并不是确定边界位置的唯一准则。我们也可以使用：最大似然估计或者最小化某一目标函数，来确定边界的位置，但是，这些方法在数学上更难以处理。

到目前为止，我们所使用的简单概率分布模型无法处理：聚类形状很复杂的情况，例如：香蕉形、轮胎形、螺旋管形的聚类。有时，一个聚类甚至可能是由好几个分散的聚类所组成的，在这种情况下，我们上面使用的分类方法可能会：将这个聚类的各个组成部分作为单独的聚类来进行处理。通常情况下，如果我们所选取的特征很合理的话，那么，简单分类方法是有效的。相反的，如果我们所选取的特征不合理，那么，即使是复杂的分类方法也于事无补。