如何求解刚体运动方程？——自动驾驶中的碰撞时间估计技术

现在，我们将在：没有关于相机运动的先验假设的情况下，应用最小二乘算法，从光流数据中，判断相机的运动情况。显然，如果所得到的方程关于所有的运动参数都是线性的，那么，最小二乘方法是最好用的。但是，不幸的是，我们找不到任何一种范数形式，使得：所得到的方程关于所有的运动参数都是线性的。再一次，我们需要处理：基于Lαβ范数的最小化问题，并使用约束条件U2+V 2+W 2=1。

我们所得到的方程是关于U、V、W、A、B和C的多项式。我们可以使用：1)标准迭代方法（例如：N ew ton法、Bairstow方法），或者，2)插值算法（例如：Regu la-Falsi方法）来进行求解。我们需要优化的目标函数为：

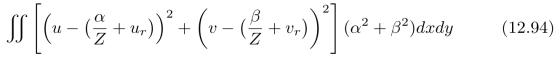
第一步是：求被积函数（即：积分号里面的表达式）关于Z的导数，然后，令求导结果等于零。于是，我们可以得到：

将式(12.95)代入式(12.94)中。我们引入Lagrange乘子，并尝试求下式的极小值，即：

(www.xing528.com)

根据极值的必要条件，分别对式(12.96)中的U、V、W、A、B、C和λ求偏导，然后令求导结果等于零，我们最终得到了：确定相机运动参数所需的方程组，即：

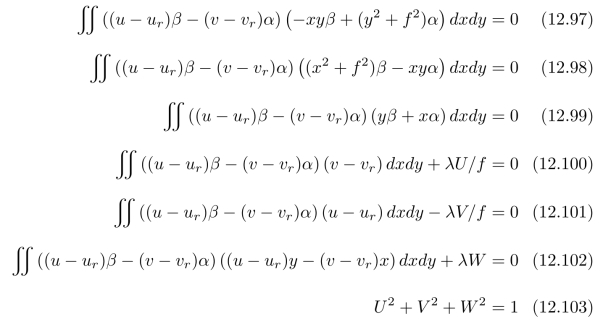
注意：在这些方程(12.97)～(12.103)中，前三个方程关于A、B和C是线性的。因此，我们可以用：含有U、V和W的表达式，来唯一地将A、B和C这三个参数表示出来。（然后，将A、B和C的表达式代入后四个方程，从而使得后四个方程中只含有U、V、W和λ）。最后，我们通过后四个方程，使用数值算法来求出U、V和W的值。这给我们提供了一个迭代算法。为进行数值求解，我们还需要将问题离散化，并导出相应的方程，在这些方程中，“积分”形式将被“求和”形式所取代。

图12.5　碰撞时间估计技术在自动驾驶中的应用。我们设计的碰撞时间估计算法计算复杂度低，可以实时运行在智能手机上。

总的来说，我们的目标是：探寻一种从光流中确定相机运动的方法，并且，允许测量数据中包含噪声。本章提出的无源导航方法满足我们的目标，并且，适于用数值方法来实现。对于某些特殊的应用，例如场景可以被近似描述为一个或多个平面的情况，我们可以尝试：直接通过图像的亮度变化来确定相机的运动信息，也就是说，不需要计算光流。相应的方法被称为直接无源导航技术^[3]。在下一小节中，我们将给出一个这方面的具体应用实例。