预测观测者运动：探究估测方法

假设我们现在正在观看一部电影，并且，假设我们已经知道：图像上每一个点的瞬时速度，即：光流，我们想要从图像序列中判断相机的运动。本章中，我们将使用整个光流场的信息，通过最小二乘方法来推导出一种确定相机运动情况的技术，称为无源导航。事实上，电影（图像序列）的形成可以被描述为如下过程：

相机和景物之间的相对运动和场景的形状（也称为景深）是生成电影（图像序列）的内因。人在看电影的过程中，不断地（根据图像序列）分析和估计场景中对应的运动和景深，也就是说，

在上一章中，我们介绍了如何估计光流场。本章中所给出的无源导航技术，使得我们最终完成了对应的视觉感知任务：从输入图像序列中获取关于场景形状和相机运动的描述信息。我们所导出的算法使用了充足的数据，具有很好的鲁棒性，并且易于数值实现。

首先，让我们来回顾一些方程。这些方程描述了：相机运动与（由相机运动所引起的）光流之间的相互关系。我们既可以假设：相机固定、场景发生变化；也可以假设：相机在静态场景中运动。我们选择使用：相机在静态场景中运动的假设。坐标系被“安放”在相机上，Z轴选为光轴。刚体运动可以被分解为两个成分：平动和（绕着某个经过原点的轴的）转动。相机的平动速度记为t；相机转动的角速度记w。场景中某一点P的瞬时坐标记为(X,Y,Z)T。虽然场景是固定的，但是，由于坐标系被安放在相机上，坐标系随着相机的运动而不断发生变化，也意味着点P的坐标随着时间而发生变化。因此，我们称其为：某一时刻的瞬时坐标。在这里，对于成像系统前面的点，都有Z＞0。

我们用r表示列向量(X,Y,Z)T，其中，上标“T”表示转置。那么，点P相对于XYZ坐标系的运动速度为：

如图12.1所示。如果我们将t和w的分量分别记为：

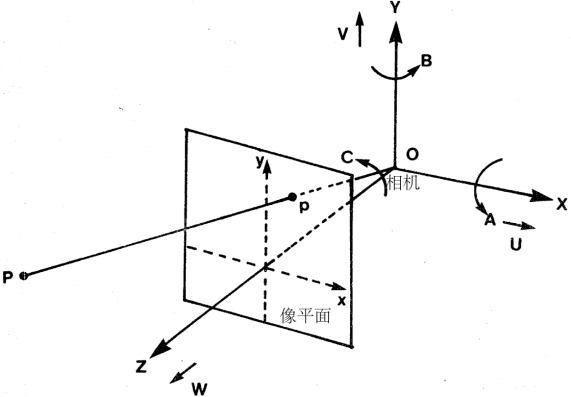
图12.1　以相机为中心的坐标系。相机的运动包括：平动和转动。平动成分t包含三个分量(U,V,W)T，分别为：沿着x-轴、y-轴和z-轴的速度；转动成分w也包含三个分量(A,B,C)T，分别为：绕着x-轴、y-轴和z-轴的角速度。

那么，我们可以将公式(12.1)写为对应的分量形式，即：

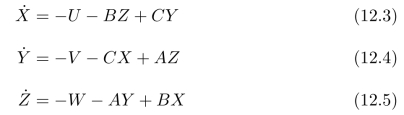(www.xing528.com)

在像平面上，每一个点的光流是指：该点上的亮度模式的瞬时速度。我们用(x,y)表示：像平面上某一个点p的坐标。这里，我们使用透视投影来确定：物体上的点P与相应的图像上的点p之间的关系。因此，p的坐标(x,y)为：

点(x,y)处的光流（记为(u,v)）为：

即x和y关于时间的导数。将x和y的具体表达式(12.6)代入，再对时间求导，我们最终可以得到：

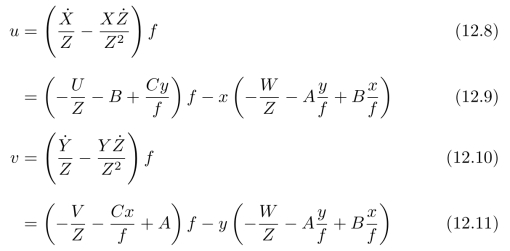
我们可以将上面两式分别写为：

其中，(ut,vt)表示：由于物体的平动所引起的光流分量；(ur,vr)表示：由于物体转动所引起的光流分量。具体表达式为：

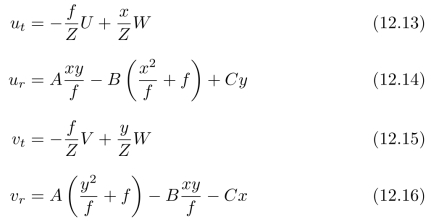
到目前为止，我们只考虑了一个点P。为了在全局上定义光流，我们假设：点P位于由函数Z(X,Y)所确定的曲面上。对于所有的X和Y，都有Z(X,Y)＞0。对于任何曲面以及相机的任何运动，我们都能相应地得到一种光流。因此，我们说：曲面以及运动产生了这个光流！

因此，光流取决于：相机运动的6个参数，以及，（与所分析的图像区域相对应的）曲面形状。图12.2中给出了：相机运动的6个参数所分别对应的光流（假设Z(x,y)为常数）。单单从光流信息中，我们能否唯一地确定这些未知量？严格地说，答案是：不能。为了说明这一点，让我们来考虑一个曲面S2，曲面S2是由S1膨胀k倍后得到的（即S1和S2是相似曲面）。进一步，令两种运动M1和M2具有相同的转动分量，并且，令它们的平动分量成比例，比例系数也为k（我们称：M1和M2为相似运动）。由S1和M1所产生的光流，等同于由S2和M2所产生的光流。根据上面给出的关于光流分量的表达式(12.13)～(12.16)，我们可以直接得出这个结论。

如果相机的运动只是单纯的平动或者转动，那么，通过光流信息恢复相机运动的问题将变得简单得多。在下面两节中，我们将分别对这两种特殊情况进行讨论。然后，我们将考虑更一般的情况，此时，我们并不知道任何有关相机运动的先验信息。