如何求解亮度为常数的局部图像区域的光流？——探讨光流计算方法

习题11.1对于一个亮度为常数的局部图像区域，由于亮度的梯度为零，因此，我们无法判断：该区域的光流。因此，我们需要使用本章中提出的方法，使用Lap lace方程，从（该区域的）边界向区域内部填充光流信息。这里，我们要研究的情况是：所填充的光流信息，正好是我们所希望得到的结果。

图11.18　部分测试结果。光流算法和无源导航技术用以估计出薄膜的运动

(a)我们让图像的亮度模式以速度(u0,v0)（在像平面上）进行运动。假设：在某一个图像区域R的内部，图像亮度为常数；并且，在区域边界∂R上的光流是精确的。证明：给定边界条件以后，通过求解Lap lace方程：

所得到的结果正好等于：区域R上的光流。提示：当且仅当光流同时满足下面两个条件，即：1)区域内的光流的Lap lace算子处理结果为零，并且，2)光流满足边界条件，我们所得到的光流才是该问题的唯一解。

(b)对于相机沿着平行于像平面（也就是说，垂直于光轴）的方向移动的情况，光流填充方法总是能够得到正确的光流吗？

(c)假设图像的“亮度模式”绕着像平面上一点(x0,y0)转动，其角速度为ω。这种情况下的光流是什么？假设对于图像中的某一个区域R，我们得到了：区域边界∂R上的光流速度的精确值，那么，给定边界条件以后，根据Lap lace方程∇2 u=0和∇2 v=0所得到的解，是否等于区域R上的光流？

(d)让我们来考虑：相机绕着光轴转动的情况。此时，光流填充方法所得到的结果总是“正确”的吗？

习题11.2假设：相机沿着光轴“撞”向一个平面物体，并且，该平面物体垂直于光轴。

(a)证明：这种情况下的光流为

其中，W表示：相机的运动速度；而Z表示：相机到平面物体的距离（注意：光流和透镜的焦距无关）。

(b)光流是静态的吗？（所谓“静态”是指：与时间无关）

(c)光流的Lap lace算子处理结果是否为零？

(d)你如何预测碰撞时间？（注意：即使我们不能恢复出：景深Z和速度W的绝对值，我们仍然能够解决这个问题。）

习题11.3这里，我们来考虑一些光流模式。这些光流模式并不是由：物体（或相机）的刚体运动所产生的。

(a)假设，你从上往下观察：一个圆形容器中的某种液体的表面。容器底部是平的，并且，在容器底部的正中央有一个洞。如果我们假设液体的高度不发生变化（尽管液体在不断地往外流），那么，光流是什么样子的？假设：光轴和液体表面垂直，并且，穿过容器底部的那个洞。提示：我们将容器中的液体看作是一个圆柱体。该圆柱体的旋转对称轴为：经过容器底部的洞并且垂直于容器底部的轴。我们以这个轴为公共轴，将圆柱体剖分为许多圆柱面，那么，流过每一个圆柱面的（液体）流量大小都是相同的。

(b)对于上面这种情况，光流的Lap lace算子处理结果是什么？是否存在奇异点^[4]？

(c)考虑三维空间中绕着某一个轴旋转的漩涡，这个漩涡的横截面是圆形对称的，既没有物质流出来，也没有物质流进去。同样，我们将这个圆面剖分成许多同心圆，同心圆的公共圆心为：漩涡的旋转轴与横截面的交点。现在假设：这些圆的“厚度”都是一样的，并且，不同半径的圆具有相同的角动量，那么，光流是什么样子的？

(d)对于上面这种情况，光流的Lap lace算子处理结果是什么？是否存在奇异点？

习题11.4现在，我们来考虑一个关于x和y的二阶多项式。如果（该多项式中）x2和y2前面的系数是：大小相等、符号相反的两个数，那么，请证明：该多项式的Lap lace算子处理结果为零。请将这个结论应用于上一题。

习题11.5假设我们使用下式：

来测量光流速度的“不连续程度”的大小，而不是使用：

那么，其相应的Eu ler方程是什么？

习题11.6证明：物体绕着任意一个轴旋转，等价于下面两个过程的“组合”：1)绕着过原点的轴旋转；2)再加上一个平移运动。并且，相应的平移运动等价于两个向量的叉积，这两个向量分别是：1)从原点到转动轴的向量、2)旋转向量。

习题11.7一个刚体绕着一个经过原点的轴转动，并且，旋转轴平行于向量w。旋转的角速度大小等于：向量w的模长。物体上的一个点r的速度等于叉积w×r，其中，r=(x,y,z)T，w=(α,β,γ)T。假设我们所使用的是正射投影模型。请证明：光流的光滑性对应于旋转物体的光滑性。请问：在轮廓处会怎么样？

提示：∇2 u、∇2 v与∇2 z之间存在什么关系？

习题11.8本题中，我们将研究：明暗和运动之间的关系。当一个物体在相机前面运动时，图像上给定点的亮度会发生变化。这是由于在不同的时刻，图像上的同一个点，对应于物体表面上的不同“小块”。这些“小块”可能具有：1)不同的反射性质，2)不同的朝向。我们现在假设：物体表面上所有的点具有相同的反射性质。因此，我们只考虑物体表面朝向的变化。现在，当一个新的“小块”进入视野时，在考虑“小块”的运动之前，我们首先必须考虑：新的“小块”的朝向和旧的“小块”有什么不同。但是，这还不够，我们必须考虑：如何通过旋转，将旧的小块“转成”新的小块。

(a)假设物体表面某一部分的移动，使得其所对应的图像“小块”在像平面（即xy平面）上的移动速度为(u,v)。那么，这个运动所产生的p和q的变化是什么？证明：亮度的变化结果为：

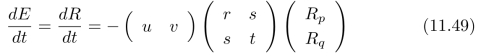
其中，r、s和t分别为：z的二阶偏导数。请将上式重新写为：图像梯度(Ex,Ey)T的形式。提示：注意，和图像中某一个像素点相对应的、物体表面上的点的x坐标，如何随时间而变化？

(b)一个刚体绕着经过原点的轴转动，并且，旋转轴平行于向量w。旋转的角速度大小等于：向量w的模长。物体表面上的一个点的坐标为r=(x,y,z)T。转动向量的分量为w=(α,β,γ)T。证明：(www.xing528.com)

现在，我们假设使用正射投影，也就是说，x′=x和y′=y。在这种情况下，由物体的运动所产生的速度场(u,v)是什么？

(c)当物体转动时，物体表面的某一个“小块”的朝向会发生变化。

请用w和 n来表示d n/dt。下一步，通过对方程：

两边求导，我们可以得到：用dp/dt和dq/dt表示的d 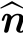n/dt。请写出其具体表达式。在式(11.51)中，

这两种关于d n/dt的表示方式是相等的，请证明下面两式：

(d)正如前面提到的，一个物体在成像系统前面旋转，图像上某一点的亮度发生变化，包含如下两个原因：

1)物体表面上具有不同朝向的曲面“小块”进入视野；

2)“小块”在运动过程中发生旋转，从而不断改变朝向。

假设速度场为(u,v)，在问题(a)中，我们计算了：原因1)对图像亮度变化的“贡献”。在问题(b)中，我们计算了：物体表面上某一点的像（在像平面上）的运动速度。在问题(c)中，我们计算了：原因2)对图像亮度变化的“贡献”。现在，请将这两个原因合并在一起，将dp/dt和dq/dt分别表示成：向量w=(α,β,γ)T的分量α,β,γ的函数形式。

习题11.9在机器视觉算法的设计过程中，我们通常在一开始的时候，首先考虑一些可控的情况，在这些情况中，答案是已知的。这通常需要使用合成图像，合成图像是基于：1)曲面形状的模型、反射率以及已知的运动情况而生成的。你需要根据已知的光流算法，生成一个合成图像序列。假设：物体表面形状是两个参数ξ和η的函数，并且，物体表面的辐射强度为L(ξ,η)。物体表面相对于观测者的平动速度为t、转动角速度为w。请描述：你如何生成合成图像序列，并且，进一步确定：其关于空间和时间的导数。最终，请编程实现计算机仿真，然后根据仿真结果完成实验报告。

习题11.10如何我们将图11.7中的“0”和“1”互换，所得到的光流估计结果是否会发生变化？请解释原因。我们将图11.7中“左边”的图像作为初始图像，“右边”的图像作为变化后的图像，可以计算出一个光流估计结果；然后，我们将图11.7中“右边”的图像作为初始图像，“左边”的图像作为变化后的图像，可以计算出另一个光流估计结果；这两个光流估计结果之间是什么关系？请解释原因。进一步，请分析上述关系成立的条件，并给出上述关系不成立的例子。

习题11.11请针对下面的两张二值图，选用4×4的窗口，使用稀疏光流法来估计光流。

然后，使用稠密光流法来估计光流。进一步，针对两种方法的光流估计结果，进行对比分析，完成研究报告。

习题11.12请针对下面的两张二值图，选用4×4的窗口，使用稀疏光流法来估计光流。

然后，再使用稠密光流法来估计光流。进一步，针对两种方法的光流估计结果，进行对比分析，完成研究报告。

习题11.13在这里，我们研究：一个旋转的球所产生的光流。球的表面的反射率是：随着球面上的点的位置而变化的。考虑一个半径为R、球心位于原点的球。这个球绕着y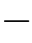轴转动，角速度为ω。我们使用正射投影模型来得到球的图像，并且，将光轴选为z轴，也就是说，x′=x和y′=y。其中，(x′,y′)是：物体表面上的点(x,y,z)T的像的坐标。通过经度ξ和维度η，我们可以确定t=0时刻球面上的一个点。坐标系随着球一起转动，因此，某一特定曲面对应于：一个固定的(ξ,η)。我们需要求出图像坐标系与球面坐标系之间的转换关系。

(a)请使用ξ和η来表示x和y。请使用x、y和t来表示ξ和η。

(b)请确定：速度场中的分量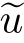 u和 v。对于时间而言，速度场是否是常数？也就是说， u和 v的函数表达式中是否包含t？

(c)请使用稠密光流算法估计光流分量u和v。所得到的结果是否与(b)问中的速度场一致？请说明其中的原因。

请设计程序完成计算机仿真，然后，根据实验结果完成研究报告。

图11.12所对应的MATLAB程序^[5]

【注释】

[1]J.Gibson于1959年提出了术语光流和运动感知问题，最终由Horn教授解决。

[2]在本章的最后一页，我们给出了：生成图11.12中结果的MATLAB程序代码。

[3]硕士研究生江伟弘、苏燮阳参与了这项工作。

[4]也就是说，液体流量大小为无穷大的地方。

[5]这段程序生成的是图11.12(a)，其中的“t=50”对应于：在式(11.40)和(11.41)中设置“λ=50”。只需将程序中的“t=50”更换为“t=0.01”，就可以得到图11.12(b)。